基本图论-连通分量(强/弱联通 割点/边 边/点双)

前言

网上现存\(60\%\)的文章都有明显的误区，本文章经过多次修改，能保证正确性

• 本文涉及强连通分量、弱连通分量、割点、割边、边双、点双，属于基本图论范畴

• 在有着直接关联的基础上又有所不同，本文基于把抽象的数组转换为在图上的意义，旨在让初学者能更轻松地理解并区分差别

• 为避免各个板子的差别过大，在正确的基础上尽量保证代码的相似性

如果您之前学过，可能与您的定义有所不同，故请在看完每个算法下面的代码后再进行文字阅读

• 文字中某个词语后出现带圆框的数字，如①②，这些词语将会在文字下方有详细的注释，方便阅读

前置

我们简略地定义\(dfs\)树为遍历路程中路径所组成的一棵树，注意下面说的儿子、叶子节点、子树边界\((\)与子树直接相连的外部节点\()\)等用法都从此基础上得出

如下图及\(dfs\)树，\(3,7\)为\(1\)的儿子，叶子节点为\(2,5,6,8\)，\(7\)的子树边界为\(\{1\}(1\)与\(7\)和\(8\)直接相连\()\)，如果新加一条边\((3,4)\)，则\(7\)的子树边界为\(\{1,3\}\)

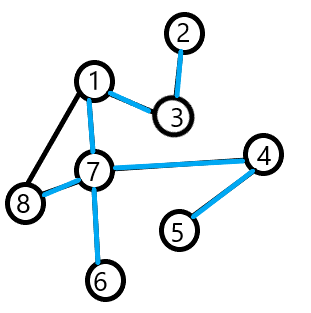
有向图

强连通分量

定义：有向图中某个点集中的点互相能到达的分量为强连通分量

为方便理解我们采取归纳法：找到完整强连通分量后立即染色

• 定义\(dfn_u\)：表示\(dfs\)中\(u\)的时间戳；初始化为第几个被遍历到的点。
• 定义\(low_u\)：表示\(u\)能到达且在\(u\)子树边界的未染色的最小时间戳①\((\)设代表该最小时间戳点的点为\(x\)，可证明\(x\)一定能与\(u\)组成强连通分量②\()\)；初始化为\(dfn_u\)。

①：显然代表该最小时间戳的不为\(u\)的子树\((\)除\(u)\)，因为子树内的时间戳\(u\)已经为最小的了。故\(u\)的子树并不影响\(low_u\)，真正影响的是\(u\)的子树外，与\(u\)子树有接触，且未染色的。

②：\((\)下图为例\()x\)位于\(f\)的左子树，\(x\)所在完整强连通内所有节点不止在左子树\((\)否则就染色了\()\)，\(x\)至少能与\(f\)组成强连通分量。故\(x\)一定能与\(u\)组成强连通分量：\(f\rightarrow u\rightarrow x\rightarrow f\)。

具体做法：在\(u\)的子树遍历完后，\(low_u=dfn_u\)则把栈顶到该点的区间染色\((\)与子树外单向联通，那\(u\)的子树未处理部分与\(u\)组成强连通分量\()\)，否则要等回到某个祖先后染色才能分量的完整

code

也可更换第\(7\)行代码为：

else if(visit[v]) low[u]=std::min(low[u],low[v]);
//此时定义low：能与u组成强连通分量(未染色)的最小时间戳

void Tarjan(LL u){
    dfn[u]=low[u]=++tim; sta[++top]=u; visit[u]=true;
    for(LL i=head[u];i;i=dis[i].nxt){
        LL v(dis[i].to);
        if(!dfn[v]){
            Tarjan(v); low[u]=std::min(low[u],low[v]);
        }else if(visit[v]) low[u]=std::min(low[u],dfn[v]);
    }
    if(low[u]==dfn[u]){
        LL now; ++nod;
        do{
            now=sta[top--]; col[now]=nod; visit[now]=false;③
        }while(now!=u);
    }
}

③：\(visit\)清空：强连通分量是建立在有向图上的，\(u\rightarrow v,v\nrightarrow u\)时，如果之前先遍历过\(v\)，则已经把\(visit\)清空了，此时\(u\)不受\(v\)的任何影响

弱连通分量

定义：同一弱连通分量里的任意两个点\(x,y\)，保证至少一方能到达另一方

想象一下某个弱连通分量进行强连通缩点后的样子？能两两到达的肯定存在于同一个大点中了，剩下的肯定是单向联通，故一定是一条单直链

性质：某一点可能属于多个弱连通分量，显然，属于强连通分量的两点一定属于同一弱连通分量

做法：在强连通缩点后的\(DAG\)图中，每一条链就是一个弱连通分量

无向图

为了割点与桥的统一计算，在无向图中我们不管父亲\((\)类似树的遍历，遇到\(f\)则\(continue)\)，稍后会说明原因

且重新定义：

• 定义\(low_u\)：\(u\)的子树与子树外接触的最小时间戳\((\)除\((u,f)\)的影响,因为在遍历\(u\)时遇到\(f\)会跳过\()\)

如下图，蓝边为\(dfs\)树，标号为时间戳，\(6\)的子树为\(\{6,7,8,9\}\)，子树与子树外的接触为\((6,3),(7,5),(9,2)\)，故\(low_6=2\)

割点

定义：无向图中，将该点从原图中拿掉后，连通分量数量增加

想象一下割点在图上的样子：一个点至少夹在两个互不接触 (( 不考虑该点的连接作用 )) 联通块之间

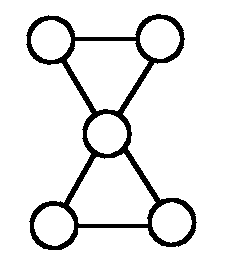
为了便于理解，先想一下暴力做法④：特判每一个点，如果该点至少有两个儿子则说明为割点\((\)这些儿子所属的子树互不接触，否则仅需遍历一次，而该点位于子树之间，显然割掉后连通块个数=儿子个数\()\)。时间复杂度\(O(nm)\)

④：因为判断儿子得把整个子树全跑一遍。而每一次判断的儿子个数仅对根有效。因为根肯定得把一个子树的点遍历完才能回溯；其他的点由于顺序关系，入度也会成为一个儿子\((\)对于无根树\()\)，实际上入度上方可能与儿子有接触，故不能一次性判断。比如下面的这幅图，从\(1\)开始遍历则\(3\)有两个儿子；但从\(3(root)\)开始遍历：\(3\longrightarrow 2\longrightarrow 1\longrightarrow 12\longrightarrow 13\longrightarrow9\longrightarrow8\longrightarrow6\longrightarrow7\longrightarrow5\longrightarrow4\longrightarrow10\longrightarrow11\)，最后得到的是\(3\)只有一个儿子，所以\(3\)不为割点

转换成条件：对于\((u,v),fa_v=u\)，在割掉\(u\)后，\(v\)的子树与外界无任何接触。也就是\(v\)的子树仅与外界的\(u\)接触，则当割掉\(u\)后，多生成了一个联通分量。

抽象成代码：\(u\in Articulation Point \longrightarrow low[v]>=dfn[u]\)

细节：如果我们首先遍历\(u(root)\)，则无论怎样\(low_v\)都会\(≥dfn_u(dfn_u=1)\)，则根据定义是把\(u\)判断为割点，其实不然⑤。

⑤：有时我们发现根不会为割点，这是为什么呢?因为\(u\)的子树就是所有点，故没有外界，也就是说特判一定满足，故该特判对其无效。

所以需要判断的是\(u\)是否有至少两个儿子\((\)原理就是上面的暴力做法\()\)，否则就为无根树上的叶子节点了\((\)也就是边界\()\)

code

void Tarjan(LL u,LL mr,LL f){
    LL rc(0);
    dfn[u]=low[u]=++cnt;
    for(LL i=head[u];i;i=dis[i].nxt){
        LL v(dis[i].to);
        if(v==f) continue;
        if(!dfn[v]){
            Tarjan(v,mr,u);
            low[u]=min(low[u],low[v]);
            if(low[v]>=dfn[u]&&u!=mr)
                cut[u]=true;
            if(u==mr) 
                rc++;
        }else low[u]=min(low[u],dfn[v]);
    }    
    if(u==mr&&rc>=2) 
        cut[mr]=true;
}

桥

定义：又称为割边，将该边从原图中拿掉后，连通分量数量增加

想象一下桥在图上的样子：一条边被两个不接触\((\)不考虑这条边的连接作用\()\)的联通块夹在中间。

如下方，两个"\(+\)点"间的为桥

为了便于理解，先想一下暴力做法：枚举每一条边\((x,y)\)从\(x\)节点出发不经过该边遍历一次，如果不能到达\(y\)则该边为桥。时间复杂度\(O(m^2)\)

转换成条件：对于桥\((u,f),fa_u=f\)的，割掉\((u,f)\)后，\(u\)的子树外界无任何接触。也就是除\((u,f)\)外，\(u\)的子树的边仅局限在内部，相当于u的子树被一根线挂在\(f\)节点上。

抽象成代码：\((u,v)\in Bridge\longrightarrow low[v]>dfn[u]\)

void Tarjan(LL u,LL f){
    dfn[u]=low[u]=++cnt;
    for(LL i=head[u];i;i=dis[i].nxt){
        LL v(dis[i].to);
        if(v==f) continue;
        if(!dfn[v]){
            Tarjan(v,u);
            low[u]=min(low[u],low[v]);
            if(low[v]>dfn[u]){
            	e[++tot][0]=u; e[tot][1]=v;
			}
        }else low[u]=min(low[u],dfn[v]);
    }
}

其实割点是可以考虑父亲的影响，而桥绝对不能

因为\(f\)为割点仅需要考虑\(u\)的子树最多遍历到\(f\)，也就是说\((u,f)\)这条边对判断起不到任何影响

而桥\((f,u)\)需要：除开这条边，\(u\)的子树最多遍历到\(u\)。如果考虑父亲的影响，\(low_u\)一定会受\(dfn_f\)的影响\((low_u=dfn_f)\)，特判起来会变得十分麻烦

故为了代码的方便，在割点割边时不考虑父亲

边双连通分量

定义：简写为边双，同一边双内，点与点的边集中无桥

如下图，每种颜色的点为一个边双，之间由桥隔开

具体做法

• 两次遍历：这个就比较简单了，直接找出所有的桥删掉，然后遍历一遍染色就行了，因为桥已经被全部删掉，故每种颜色的分量的边集中肯定无桥

• 一次遍历：桥的定义入手，考虑桥\((f,u)\)，\(u\)的子树局限于内部，故满足\(low_u=dfn_u\)；而同属\(u\)的边双内的任意点\(x\)，由于无桥，肯定不会局限于\(x\)的子树，故满足\(low_x≠dfn_x\)。与强连通分量的做法类似，判断\(dfn_u=low_u\)，把压进栈里的点取出来染色即可

void Tarjan(LL u,LL fa){
    dfn[u]=low[u]=++tim; sta[++top]=u;
    for(LL i=head[u];i;i=dis[i].nxt){
        LL v(dis[i].to);
        if(v==fa) continue;
        if(!dfn[v]){
            Tarjan(v,u); low[u]=std::min(low[u],low[v]);
        }else low[u]=std::min(low[u],dfn[v]);
    }
    if(low[u]==dfn[u]){
        LL now; ++nod;
        do{
            now=sta[top--]; col[now]=nod;
        }while(now!=u);
    }
}

点双连通分量

定义：简写为点双，对于同属一个点双的任意点，删除后，该分量中的点仍能互相到达；或者说仅对于该分量而言，无割点。

具体做法：
依旧从割点的定义入手：割点将原图分成互不相连的多个联通块，显然每个联通块本身已经是一个点双了，但不完整，因为相邻的割点在边界，如果与联通块共同组成一个新联通块，割掉后也不会另外产生联通块\((\)相当于该连通块上的叶子节点\()\)，所以需要加上来才完整\((\)故割点是会同时存在于多个点双中的\()\)

我们怎么染色呢？可以发现在\(dfs\)树中，割点\(u\)在进行与儿子节点的染色时会分给多个点双，而在遍历完儿子后，与祖先将仅产生一个完整点双⑥。所以当\(u\)为割点，给儿子节点染色时，取到儿子借点就够了，栈中保留\(u\)，等到\(u\)的某个祖先后再取出来。

新建一个节点来维护某个点双，该点向该点双的每个点连一条边\((\)当然这是建立在新图上的\()\)，这就是广义圆方树

⑥：如下图

void Tarjan(LL u){
    dfn[u]=low[u]=++tim; sta[++sta[0]]=u;
    for(LL i=G1.head[u];i;i=G1.dis[i].next){
        LL v(G1.dis[i].to);
        if(!dfn[v]){
            Tarjan(v);
            low[u]=min(low[u],low[v]);
            if(low[v]>=dfn[u]){
                G2.Add(++tot,u); LL now(0);
                do{
                    now=sta[sta[0]--];
                    G2.Add(tot,now);
                }while(now!=v);
            }
        }else low[u]=min(low[u],dfn[v]);
    }
}

例题一：[HNOI2012]矿场搭建

我们把每个点双看作一个分量

• 分量无割点：说明整个联通块就是一个点双，建两个出口，随便割一个由于点双的性质所有点都能出去

• 分量有一个割点：在除割点的地方建一个出口，割掉割点直接去分量里的出口，割掉出口通过割点跑到其他分量的出口中

再具体点就相当于多个点双构成了一棵树\((\)仅一个节点的树除外\()\)，而我们仅在叶子节点建出口

例题二：[POI2008]BLO-Blockade

显然仅割点会对除本身以外的访问有影响，影响为多个分支所跨该割点访问数，

记分支的节点数分别为\(size_1,size_2,...,size_k\)，\(sum=\sum\limits_{i=1}^k size_i,ans=\sum\limits_{i=1}^k size_i\cdot(sum-size_i)+(n-1)*2\)

例题三：[ZJOI2004]嗅探器

其实就是求：多个点双构成的树，\(x,y\)所在节点间的割点

• 首先得所属节点不同：\(low_y>=dfn_x\)

• 其次得保证\(u\)是位于期间的割点：\(dfn_u<=low_v\)

• 且\(u\)的该分支\(v\)，\(y\)存在于子树\(v\)内：\(dfn_v<=dfn_y\)

例题四：HDU - 5215

纯奇环偶环通过dfs树上，染色判断（由于偶环可能有两个奇环，通过一点相交，dfs树上并不能判完）

两环如果相交必定形成偶环，由于不可以重复经过边，把每个边双提出来判断一下是否存在两个环以上即可

code