图（基本介绍）

1.为什么要有图

1)线性表局限于一个直接前驱和一个直接后继的关系

2)树也只能有一个直接前驱也就是父节点

3)当我们需要表示多对多的关系时， 这里我们就用到了图

2.图的举例说明

图是一种数据结构，其中结点可以具有零个或多个相邻元素。两个结点之间的连接称为边。
结点也可以称为顶点。如图：

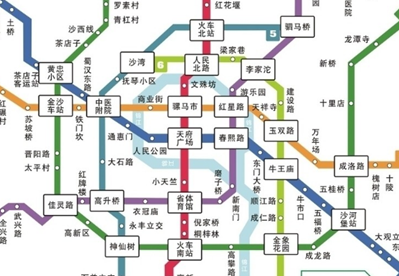
3.图的常用概念

1)顶点(vertex)

2)边(edge)

3)路径

4)无向图(上图)

5)有向图

6)带权图

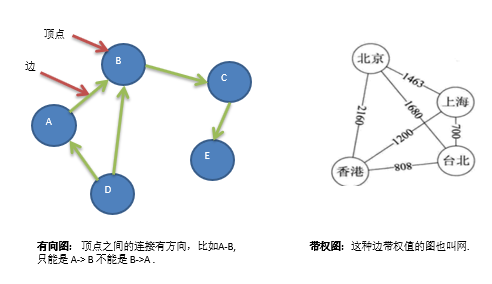
4.图的表示方式

图的表示方式有两种：二维数组表示（邻接矩阵）；链表表示（邻接表）。

4.1邻接矩阵

邻接矩阵是表示图形中顶点之间相邻关系的矩阵，对于n个顶点的图而言，矩阵是有row和col表示的是1....n个点。

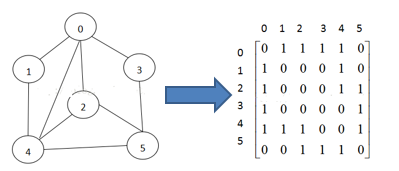
4.2邻接表

1)邻接矩阵需要为每个顶点都分配n个边的空间，其实有很多边都是不存在,会造成空间的一定损失.

2)邻接表的实现只关心存在的边，不关心不存在的边。因此没有空间浪费，邻接表由数组+链表组成

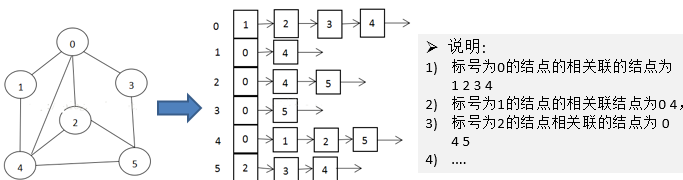
5.图的快速入门案例

要求: 代码实现如下图结构.

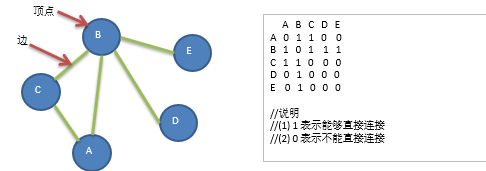
思路分析

(1) 存储顶点String 使用 ArrayList

(2) 保存矩阵 int[][] edges

6.图的创建代码实现

package com.yt.graph;

import java.lang.reflect.WildcardType;
import java.util.ArrayList;
import java.util.Arrays;

public class Graph {

	private ArrayList<String> vertexList;//存储顶点集合
	private int[][] edges;//存储图对应的领接矩阵
	private int numOfEdges;//表示边的数目
	
	public static void main(String[] args) {
		// 测试图的创建
		int n = 5;//结点的个数
		String vertexs[] = {"A", "B", "C", "D", "E"};
		//创建图
		Graph graph = new Graph(n);
		//添加结点
		for(String vertex : vertexs){
			graph.insertVertex(vertex);
		}
//		graph.showGraph();//没有添加边，输出的全部是0
		// 添加边 案例中的图 A-B A-C B-C B-D B-E
		graph.insertEdges(0, 1, 1);
		graph.insertEdges(0, 2, 1);
		graph.insertEdges(1, 2, 1);
		graph.insertEdges(1, 3, 1);
		graph.insertEdges(1, 4, 1);
		//显示邻接矩阵
		graph.showGraph();

	}
	
	// 构造器，进行初始化，
	// n表示结点的个数
	public Graph(int n){
		//初始化矩阵和vertexList
		edges = new int[n][n];
		vertexList = new ArrayList<String>(n);
		numOfEdges = 0;		
	}
	// 图中常用的方法
	// 返回结点的个数
	public int getNumOfVertex(){
		return vertexList.size();
	}
	//得到边的数目
	public int getNumOfEdges(){
		return numOfEdges;
	}
	//返回结点i(下标)对应的数据0->"A" 1->"B" 2->"C"
	public String getValueByIndex(int i){
		return vertexList.get(i);
	}
	//返回v1和v2之间的权值
	public int getWeight(int v1, int v2){
		return edges[v1][v2];
	}
	//显示图对应的矩阵
	public void showGraph(){
		for(int[] link : edges){
			System.out.println(Arrays.toString(link));//一排一排的输出来
		}
	}
	
	//插入结点
	public void insertVertex(String vertex){
		vertexList.add(vertex);
	}
	// 添加边
	/**
	 * 
	 * @param v1 表示点的下标，是第几个顶点
	 * @param v2 第二个顶点对应的下标
	 * @param weight 两个顶点之间的权重
	 */
	public void insertEdges(int v1, int v2, int weight){
		edges[v1][v2] = weight;
		edges[v2][v1] = weight;
		numOfEdges++;
	}
	

}