点分治——POJ 1741
写的第一道点分治的题目,权当认识点分治了。
点分治,就是对每条过某个点的路径进行考虑,若路径不经过此点,则可以对其子树进行考虑。
具体可以看menci的blog:点分治
来看一道例题:POJ 1741 Tree
题目大意:扔给你一颗有权无根树,求有多少条路径的长度小于k;
解题思路:先找出重心,用一次dfs处理出每个点到根的距离dis,然后将dis[]排序,用O(n)的复杂度处理出"过根且长度小于等于k的路径数目",删除根节点,对于每棵子树重复上述操作。
注意要去重:
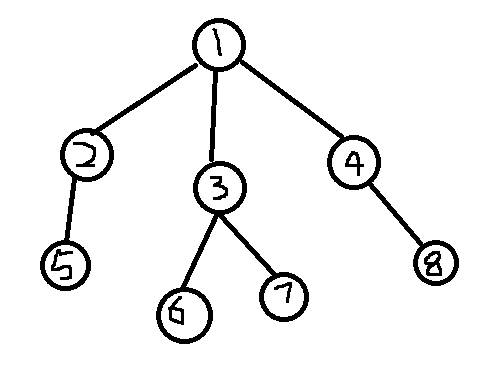
像上面这样一个图,假设每条边的长度为1,即点到根的路径长等于点的深度,设k=4。此时dis[6]=2,dis[7]=2;dis[6]+dis[7]=4=k。但是当分治以③为根节点的子树时,dis[6]+dis[7]=2<k,这样6->7这条路径就被计算了两次,所以每次求完过根节点的符合条件的路径数之后,要减去在同一棵子树下的节点之间的符合条件的路径数。
代码:
1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 using namespace std; 5 6 struct edge{ 7 int to,next,w; 8 }e[20030]; 9 10 int root,ans,u,v,l,n,kk,ne,size; 11 int head[10009],s[10009],d[10009],dis[10009],f[10009]; 12 //s[k]为k的子节点数目,dis[k]为k到根节点的距离 13 bool b[10009]; 14 15 void add(int a,int b,int c){ 16 e[++ne].to=b; e[ne].w=c; e[ne].next=head[a]; head[a]=ne; 17 } 18 19 void getroot(int k,int fa){ 20 int v,i; 21 s[k]=1; 22 f[k]=0; 23 for(i=head[k];i!=-1;i=e[i].next){ 24 v=e[i].to; 25 if(v!=fa&&!b[v]){ 26 getroot(v,k); 27 s[k]+=s[v];//递归求子节点数目 28 f[k]=max(f[k],s[v]); 29 } 30 } 31 f[k]=max(f[k],size-s[k]);//dp求重心 32 if(f[k]<f[root])root=k; 33 } 34 35 void getdis(int k,int fa){ 36 int i,v; 37 d[++d[0]]=dis[k];//储存距离以便排序 38 for(i=head[k];i!=-1;i=e[i].next){ 39 v=e[i].to; 40 if(v!=fa&&!b[v]){ 41 dis[v]=dis[k]+e[i].w;//dfs求距离 42 getdis(v,k); 43 } 44 } 45 } 46 47 int clac(int k,int init){ 48 int i,j,ret=0; 49 d[0]=0; 50 dis[k]=init; 51 getdis(k,0); 52 sort(d+1,d+1+d[0]); 53 for(i=1,j=d[0];i<j;) 54 if(d[i]+d[j]<=kk)ret+=j-i++;//计算路径数 55 else j--; 56 return ret; 57 } 58 59 60 void work(int k){ 61 int v,i; 62 ans+=clac(k,0);//计算路径数并加在ans上 63 b[k]=true;//标记重心为删除 64 for(i=head[k];i!=-1;i=e[i].next){ 65 v=e[i].to; 66 if(!b[v]){ 67 ans-=clac(v,e[i].w);//去重 68 f[0]=size=s[v]; 69 getroot(v,root=0);//更新重心 70 work(root);//对子树求解 71 } 72 } 73 } 74 75 int main(){ 76 int i; 77 while(scanf("%d%d",&n,&kk)==2){ 78 if(n==0&&kk==0)break; 79 for(i=1;i<=n;i++){ 80 head[i]=-1; 81 b[i]=0; 82 } 83 ne=0; 84 for(i=1;i<=n-1;i++){ 85 scanf("%d%d%d",&u,&v,&l); 86 add(u,v,l); 87 add(v,u,l);//注意要连双向边 88 } 89 root=0; 90 f[0]=size=n; 91 getroot(1,0);//求重心 92 ans=0; 93 work(root); 94 printf("%d\n",ans); 95 } 96 return 0; 97 }
总体上感觉点分治不是很难理解,只要对题目有思路应该能写出来。(orz就是写代码经常出错!b[v]写成!b[k]之类的还查不出来)


