边分治学习笔记
本文参考自:https://oi-wiki.org/graph/tree-divide/#_2
https://www.cnblogs.com/Miracevin/p/10739810.html
边分治:顾名思义就是对边进行分治
具体过程类似点分:就是找一条边将这棵树尽可能均匀的分成两半,然后分别递归
但是遇到菊花图就完蛋了
所以我们可以像线段树那样,建立虚点,俗称三度化
见下图
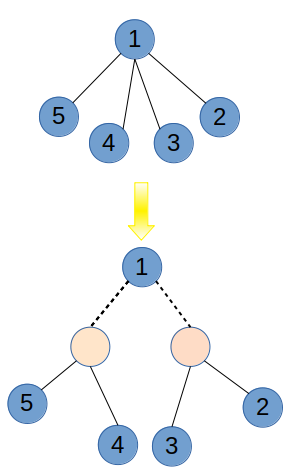
然后再进行边分治,时间复杂度就对了
有朋友可能要问了:能点分为啥要边分?
这里就要发现边分治最重要的性质,如果你类似点分树那样,把边看成点,然后递归下去建树,你将得到一颗边分树,然后你会发现这是一棵二叉树!!!
二叉树能干吗,能干的事多了.
比如合并,还有只有两个儿子可以黑白染色,方便计算距离
总结一下几个性质
- 树高是log级别的
- 是二叉树
- 非叶子节点都是边,叶子节点是点
- 原树中$dist_{x,y}$ = x到边分树中lca(x,y)的实际距离 + y到边分树中lca(x,y)的实际距离
看下面几 两道例题
原题给了你两棵树,要你求$max$ ($d1_x$ + $d1_y$ - $d1_{lca(x,y)}$ - $d2_{lca(x,y)}$)
d1,d2表示在两颗树中的深度.
考虑改写条件 $ans$ = $max$ ($\frac{1}{2}$ ($dist1_{x,y}$ + $d1_x$ + $d1_y$ - 2 * $d2_{lca(x,y)}$))
我们考虑在第一棵树上进行边分治,对于每个非叶子节点,不妨设该非叶子节点代表的边位$(a,b)$,暴力维护左子树内$dist1_{x,a}$ + $d1_{x}$的最大值,和右子树内$dist1_{y,b}$ + $d1_{y}$的最值,因为树高是log所以暴力的时间复杂度是$O(nlogn)$
我们发现答案的前三项我们已经维护好了.接下来应该就是枚举$lca2(x,y)$了,设为z,我们要在第一棵树上计算满足$lca2(x,y)$ == z的点对,然后用前面所维护的信息来更新答案.
怎么计算呢?这时候,边分树的优越性就体现出来了,我们可以刚开始,维护第一棵树中n条从根到叶子节点的链,然后dfs第二棵树,每访问到第二棵树的一条边(x,y),就把x,y所对应的边分树(链)合并起来.因为是二叉树,所以用线段树合并的方法合并,时间复杂度就是对的,$O(nlogn)$,边合并边计算即可.
人死了,写了一晚上,死活85分,MLE
代码将就看吧,

/*CTSC2018暴力写挂*/ #include<bits/stdc++.h> using namespace std; #define ll long long #define debug puts("hxsb") #define bad exit(0) #define Debug(x) cout<<x<<endl; ll read(){ char c = getchar(); ll x = 0;int f = 1; while(c < '0' || c > '9') f = (c == '-')?-1:f,c = getchar(); while(c >= '0' && c <= '9') x = x * 10 + c - 48,c = getchar(); return x * f; } const int N = 4e5 + 10; typedef pair<int,ll> pii; #define pb push_back #define mp make_pair #define fi first #define se second int n,m,cnt;/*原树中的点数,三度化后的点数,边分树上的点*/ ll ans = -1e18; int ch[N<<2][2];int e[N<<2][2];int Fa[N<<2];ll W[N<<2]; bool fuck = 0; const ll inf = 1e18; struct Edge_Divide_Tree{ int ch[2]; ll vl,vr,w; }t[N<<5];int root,num; int rt[N<<2]; int merge(int u,int v,ll nowd){ if(!u || !v) return u | v; // assert(t[u].w == t[v].w); ans = max(ans,max(t[u].vl + t[v].vr,t[u].vr + t[v].vl) + t[u].w - 2 * nowd); t[u].vl = max(t[u].vl,t[v].vl); t[u].vr = max(t[u].vr,t[v].vr); t[u].ch[0] = merge(t[u].ch[0],t[v].ch[0],nowd); t[u].ch[1] = merge(t[u].ch[1],t[v].ch[1],nowd); return u; } namespace Tree1{/*先建出点分树,以及它的m条链*/ vector<pii>e1[N<<2]; int tot = 1; int head[N<<2]; bool used[N<<2]; struct Edge{ int nxt,point; ll w; }edge[N<<2]; void add_edge(int u,int v,int w){ edge[++tot].nxt = head[u]; edge[tot].point = v; edge[tot].w = w; head[u] = tot; } int r1,r2,mx,siz[N<<2];ll w;int cen; ll dis[N<<2];int anc[N<<1][21],dep[N<<1];int st[N<<1],top; bool vis[N<<2]; void rebuild(int x,int fa){ int sz = 0;vis[x] = 1; for(int i = 0; i < (int)e1[x].size(); ++i){ int y = e1[x][i].fi; if(!vis[y]){ sz++; } } // cout<<x<<' '<<sz<<endl; if(sz <= 2){ for(int i = 0; i < (int)e1[x].size(); ++i){ int y = e1[x][i].fi; if(!vis[y]){ // e2[x].pb(mp(y,e1[x][i].se)); add_edge(x,y,e1[x][i].se); add_edge(y,x,e1[x][i].se); // e2[y].pb(mp(x,e1[x][i].se)); rebuild(y,x); } } return; } else{ int s1 = ++m,s2 = ++m; add_edge(x,s1,0);add_edge(s1,x,0); add_edge(x,s2,0);add_edge(s2,x,0); for(int i = 0; i < (int)e1[x].size(); ++i){ int y = e1[x][i].fi; if(!vis[y]){ if(i & 1) e1[s1].pb(e1[x][i]); else e1[s2].pb(e1[x][i]); } } if(e1[s1].size()) rebuild(s1,fa); if(e1[s2].size()) rebuild(s2,fa); } } void getrt(int u,int fa,int S){ siz[u] = 1; for(int i = head[u]; i; i = edge[i].nxt){ int v = edge[i].point; if(v ^ fa && !used[i]){ getrt(v,u,S); siz[u] += siz[v]; int res = max(siz[v],S - siz[v]) ; if(res < mx) r1 = u,r2 = v,mx = res,cen = i,w = edge[i].w; } } } void dfs(int u,int fa){ anc[u][0] = fa; dep[u] = dep[fa] + 1; for(int i = 1; i <= 19; ++i) anc[u][i] = anc[anc[u][i-1]][i-1]; for(int i = head[u]; i; i = edge[i].nxt){ int v = edge[i].point; if(v ^ fa && !used[i]) { dis[v] = dis[u] + edge[i].w; dfs(v,u); } } } int lca(int x,int y){ if(dep[x] < dep[y]) swap(x,y); for(int i = 19; ~i; --i) if(dep[anc[x][i]] >= dep[y]) x = anc[x][i]; if(x == y) return x; for(int i = 19; ~i; --i){ if(anc[x][i] != anc[y][i]) x = anc[x][i],y = anc[y][i]; } return anc[x][0]; } ll Dist(int x,int y){ return dis[x] + dis[y] - 2 * dis[lca(x,y)]; } int build(int u,int fa,int S){ r1 = 0,r2 = 0,mx = 1e9; getrt(u,fa,S); used[cen] = used[cen^1] = 1; if(S == 1) return u; int p = ++cnt; W[p] = w; int sr2 = siz[r2]; int R1 = r1,R2 = r2; ch[p][0] = build(R1,R2,S-sr2); e[p][0] = R1; ch[p][1] = build(R2,R1,sr2); e[p][1] = R2; Fa[ch[p][0]] = Fa[ch[p][1]] = p; // cout<<p<<' '<<ch[p][0]<<' '<<ch[p][1]<<' '<<R1<<' '<<R2<<' '<<W[p]<<endl; return p; } void ins(int &p,int u,int leaf){ if(!p) p = ++num; if(top == 0){ // assert(u == leaf); return; } int op = st[top];top--; t[p].vl = t[p].vr = -inf; if(op == 0){ int r = e[u][0]; t[p].vl = Dist(r,leaf) + dis[leaf]; t[p].w = W[u]; ins(t[p].ch[0],ch[u][0],leaf); } else{ int r = e[u][1]; t[p].vr = Dist(r,leaf) + dis[leaf]; t[p].w = W[u]; ins(t[p].ch[1],ch[u][1],leaf); } } void solve(){ n = read(); m = n; for(int i = 1; i < n; ++i){ int x = read(),y = read();ll w = read(); e1[x].pb(mp(y,w));e1[y].pb(mp(x,w)); } rebuild(1,0); dfs(1,0); cnt = m;mx = 1e9; r1 = 0,r2 = 0; root = build(1,0,m); /*bad;*/ for(int i = 1; i <= m; ++i){ int u = i; while(Fa[u]){ st[++top] = (ch[Fa[u]][1] == u); u = Fa[u]; } ins(rt[i],root,i); } } } namespace Tree2{ vector<pii>e[N<<2]; ll dis[N]; void getdata(){ for(int i = 1; i < n; ++i){ int x = read(),y = read();ll w = read(); e[x].pb(mp(y,w));e[y].pb(mp(x,w)); } } void dfs(int x,int fa){ ans = max(ans,2*(Tree1::dis[x] - dis[x])); for(int i = 0; i < (int)e[x].size(); ++i){ int y = e[x][i].fi; if(y ^ fa){ dis[y] = dis[x] + e[x][i].se; dfs(y,x); rt[x] = merge(rt[x],rt[y],dis[x]); } } } } int main(){ // freopen("wronganswer18.in","r",stdin); Tree1::solve(); Tree2::getdata(); Tree2::dfs(1,0); assert(ans % 2 == 0); printf("%lld\n",ans>>1); return 0; }
真.暴力写挂
2.WC2018通道
简要题意,给定三棵带权树,要你求最大的点对a,b使得最大化$dist1_{(a,b)}$ + $dist2_{(a,b)}$ + $dist3_{(a,b)}$.
边权是正的,n <= 1e5
先考虑两棵树怎么做,显然$dist1_{a,b}$ + $dist2_{a,b}$ = $d1_{a}$ + $d1_{b}$ - 2 * $d1_{lca(a,b)}$ + .....(第二棵树同理)
于是我们可以把在第二棵树下面挂虚点,边权为$d1_{x}$,然后我们可以dfs第一棵树,每遍历一个lca,就合并它不同子树在第二棵树上的点集的最大值,因为这等价于直径,所以可以合并
考虑多一棵树怎么做,我们考虑对第一颗树边分,然后区分黑点,白点,对第二棵树建虚树,同样在第三棵树上插虚点(不需要显式建出来,只要利用其可以合并的性质算就可以了),然后就可以做了.(注意直径的两端必须是黑白点,即在边分树枚举到的lca的两端)
因为边分树树高是logn的,所以我们只需要多一个log的代价就可以做了,时间复杂度$O(nlogn)$.
代码咕咕(太难写了)
最后总结一下容易写挂的地方
- 数组要开4倍
- 重构树(三度化)的过程中要记得标记走过的点不能走,而不仅仅是父亲不能走(因为在重构树上的父亲可能不是原树中有边相连的父亲)
- 边分治的过程中,要像点分治那样开个bool型数组,记录下哪些边已经被作为中心边了,接下来不能走



