学习日志3
上一篇学习日志因为春节贪玩 鸽了,希望这篇不要再这样了
Need to do
- 边分治学习笔记(完成)
- CTSC2018暴力写挂(完成)
- 十二省联考皮配题解
- 完成模拟赛T3(这个实在不会)
- 单位根反演学习(完成)
- 网络流深入学习
- 补模拟赛T2(完成)
- 复习burnside/Polya定理,(群论学习先咕咕吧,不会)
- 数学:学习线性代数:矩阵可对角化\特征根和特征多项式
- 完成blog:一类积性函数求和的方法
upd.2021.2.21
希望今\明天能打起状态来,be confident about yourself
本来想学点东西的,结果调题调了1个晚上
upd 2021.2.22
晚上target
- 完成T2题解(完成)
- 改T3(不会树分块,爬了,不过链上/序列的的求若干满足条件的二/三元组,可以往分治/分块方面想)
- 写一下昨天模拟赛的简要题解
- 学习线性代数:矩阵可对角化\特征根和特征多项式(简单学习了一下,深刻觉得想用这玩意解3阶递推式的我一定是脑子有问题,推一个递推式推了1h多还推错了.jpg)
- 完成至少一道网络流建模题
一道精妙的数学题
- 给定两个数列{$a_n$},{$b_n$},$a_0$ = $0$,$b_0$ = $1$
- $a_n$ = $x$$a_{n-1}$ - $y$$b_{n-1}$
- $b_n$ = $x$$b_{n-1}$ + $y$$a_{n-1}$
- 求a,b通项
一句话题解,设$c_n$ = $a_n$ + $i$$b_n$,i为虚数单位,则有$c_n$ = $(x + y_i)^n$
很巧妙的构造
市内模拟赛简要题解
套路题,我们将询问离线,用扫描线,同时用LCT维护parent树,就是每扫描到一个点,就access一遍,更新这些点当前最长的前缀是哪里,用线段树维护当前点到每个点的区间的前缀的最长公共后缀,在access的过程中顺便更新即可.
容易发现,你怼大佬的时间和回血是无关的,所以我们可以先dp一下你最多可以怼大佬的次数,然后可以bfs出你可以造成的伤害(如果需要全局的值,并且希望其满足某种单调性,用bfs要比dfs好),hash判重,注意到状态数不多,(最多去重完1e6左右,实际数据远远不到)
然后就变成一个在数列上是否存在满足若干条件的2元组,排序完双指针即可.
3.[清华集训2016]Alice and Bob又在玩游戏
一个重要的套路题(ix35鸽鸽说的)
显然这是一个公平博弈游戏,于是我们考虑SG函数,考虑对于x的子树求SG[x],根据multi_SG定理,我们要枚举删除的是哪个点,然后对得到的SG值作mex
考虑至下而上合并,发现如果删除x自己,SG值就是$Xor_u$($u \in son_x$),如果是删除的点在某个儿子的子树内,不妨设其为v,那么新的SG值显然是其在v中的SG值异或上所有兄弟的SG值的异或和
发现对于所有在v子树内的删除方法,转移都一样,于是考虑用每个点建一个Trie维护SG集合,支持全局Xor,支持合并(父亲与儿子合并,先对儿子全局Xor再合并),查询mex值即可
代码:

#include<bits/stdc++.h> using namespace std; int read(){ int x = 0;char c = getchar(); while(c < '0' || c > '9') c = getchar(); while(c >= '0' && c <= '9') x = x * 10 + c - 48,c = getchar(); return x; } const int N = 2e5 + 10; #define T 17 bool fuck = 0; struct Edge{ int nxt,point; }edge[N<<1]; int head[N],tot,n,m; void add_edge(int u,int v){ edge[++tot].nxt = head[u]; head[u] = tot; edge[tot].point = v; } int rt[N]; struct Trie{ int ch[N<<5][2],cnt,tag[N<<5],siz[N<<5];int st[N],top; void init(){ memset(ch,0,sizeof(ch)); cnt = 0;top = 0; memset(siz,0,sizeof(siz)); memset(tag,0,sizeof(tag)); } void pushup(int p){ siz[p] = siz[ch[p][0]] + siz[ch[p][1]]; } void pushmark(int p,int bit){ if(!tag[p]) return; if(tag[p] & (1 << bit)) swap(ch[p][0],ch[p][1]); tag[ch[p][0]] ^= tag[p];tag[ch[p][1]] ^= tag[p]; tag[p] = 0; } void ins(int x,int id){ if(!rt[id]) rt[id] = ++cnt; int p = rt[id]; for(int i = T; i >= 0; --i){ pushmark(p,i);st[++top] = p; int c = ((x & (1 << i)) > 0); if(!ch[p][c]) ch[p][c] = ++cnt; p = ch[p][c]; }siz[p] = 1; while(top){ pushup(st[top]),top--; } } int merge(int u,int v,int bit){ if(!u || !v) return u | v; if(bit == -1){ // assert(siz[u] == 1 && siz[v] == 1); return u; } pushmark(u,bit);pushmark(v,bit); ch[u][0] = merge(ch[u][0],ch[v][0],bit-1); ch[u][1] = merge(ch[u][1],ch[v][1],bit-1); pushup(u); return u; } int mex(int u){ int p = rt[u]; int ans = 0; for(int i = T; i >= 0; --i){ pushmark(p,i); if(siz[ch[p][0]] != (1 << i)){ p = ch[p][0]; } else{ p = ch[p][1]; ans += (1 << i); } } return ans; } }trie; bool vis[N]; int sg[N]; void dfs(int u,int fa){ vis[u] = 1; int _sg = 0; for(int i = head[u]; i ; i = edge[i].nxt){ int v = edge[i].point; if(v ^ fa){ dfs(v,u); _sg ^= sg[v]; } } trie.ins(_sg,u); for(int i = head[u]; i ; i = edge[i].nxt){ int v = edge[i].point; if(v ^ fa){ // cout<<u<<' '<<v<<' '<<(_sg ^ sg[v])<<endl; trie.tag[rt[v]] ^= (_sg ^ sg[v]); rt[u] = trie.merge(rt[u],rt[v],T); } } sg[u] = trie.mex(u); } void solve(){ n = read(),m = read(); tot = 0; memset(vis,0,sizeof(vis)); memset(head,0,sizeof(head)); memset(rt,0,sizeof(rt)); trie.init(); for(int i = 1; i <= m; ++i){ int u = read(),v = read(); add_edge(u,v);add_edge(v,u); } int ans = 0; for(int i = 1; i <= n; ++i){ if(!vis[i]){ dfs(i,0); ans ^= sg[i]; } } if(ans) puts("Alice"); else puts("Bob"); } int main(){ freopen("data.in","r",stdin); freopen("data.out","w",stdout); int t = read(); while(t--) solve(); return 0; }
upd 2.28
HDU 6405 Make ZYB Happy
近似于广义SAM模板?
具体怎么做就不说了,广义后缀自动机有以下性质:
- 设$End_{i,j}$为第i个字符串,第j个前缀在SAM上的点,n为字符串长度总和,则每个点暴力往上跳,计算SAM每个点包含了多少不同字符串的时间复杂度是$O(n\sqrt n)$
- 证明主要是我们考虑对于一个长度为m的字符串,设S为后缀自动机节点数,它遍历的点数 $\leq$ $min(m^2,S)$,$m^2$是因为总共最多$m^2$个子串,均摊以下即可得到以上结果

/*Make ZYB Happy*/ #include<iostream> #include<algorithm> #include<cstdlib> #include<cstring> #include<cstdio> using namespace std; #define ll long long int read(){ char c = getchar(); int x = 0; while(c < '0' || c > '9') c = getchar(); while(c >= '0' && c <= '9') x = x * 10 + c - 48,c = getchar(); return x; } const int N = 1e6 + 10; const int mod = 1e9 + 7; struct SAM{ int ch[27]; int len,fa; }sam[N<<2]; int w[N<<2],a[N<<2]; vector<int>End[N]; int ans[N],mi[N],sum[N]; #define pb push_back int lst = 1,cnt = 1; char s[N]; int vis[N]; int qpow(int x,int y){ int ans = 1; while(y){ if(y & 1) ans = 1ll * ans * x % mod; x = 1ll * x * x % mod; y >>= 1; } return ans; } void ins(int c){ if(sam[lst].ch[c] && sam[lst].len + 1 == sam[sam[lst].ch[c]].len){ lst = sam[lst].ch[c]; return; } int p = lst,np = lst = ++cnt; sam[np].len = sam[p].len + 1; for(; p && !sam[p].ch[c]; p = sam[p].fa) sam[p].ch[c] = np; if(!p) sam[np].fa = 1; else{ int q = sam[p].ch[c]; if(sam[q].len == sam[p].len + 1) sam[np].fa = q; else{ int nq = ++cnt; if(p == lst) lst = nq; sam[nq] = sam[q]; sam[q].fa = sam[np].fa = nq; sam[nq].len = sam[p].len + 1; for(; p && sam[p].ch[c] == q; p = sam[p].fa) sam[p].ch[c] = nq; } } } void add(int &x,int y){ x += y - mod; x += (x >> 31) & mod; } void calc(int u,int T){ if(vis[u] == T) return; if(!u) return; vis[u] = T; w[u] = 1ll * w[u] * a[T] % mod; calc(sam[u].fa,T); } int main(){ int n = read(); for(int i = 1; i <= n; ++i){ scanf("%s",s+1); int m = strlen(s+1); End[i].pb(0); lst = 1; for(int j = 1; j <= m; ++j){ ins(s[j]-'a'); End[i].pb(lst); } } for(int i = 1; i <= cnt; ++i) w[i] = 1; mi[0] = 1; for(int i = 1; i <= 1e6; ++i) mi[i] = 1ll * mi[i-1] * 26 % mod; for(int i = 1; i <= 1e6; ++i) sum[i] = sum[i-1],add(sum[i],mi[i]); for(int i = 1; i <= n; ++i) a[i] = read(); for(int i = 1; i <= n; ++i){ for(int j = 1; j < (int)End[i].size(); ++j){ calc(End[i][j],i); } } for(int i = 2; i <= cnt; ++i){ int l = sam[sam[i].fa].len + 1,r = sam[i].len; add(ans[l],w[i]);add(ans[r+1],(mod-w[i])%mod); } for(int i = 1; i <= 1e6; ++i) add(ans[i],ans[i-1]); for(int i = 1; i <= 1e6; ++i) add(ans[i],ans[i-1]); int q = read(); while(q--){ int m = read(); printf("%lld\n",1ll * ans[m] * qpow(sum[m],mod-2) % mod); } return 0; }
upd 3.1
考虑$\frac{n}{m}$满足什么条件在k进制下是纯循环的,首先我们钦定gcd(n,m) == 1,否则可以得到更简的分数,容易发现商循环等价于余数循环,解一个简单的同余方程,可以发现充要条件是gcd(m,k) == 1
然后推导过程如下: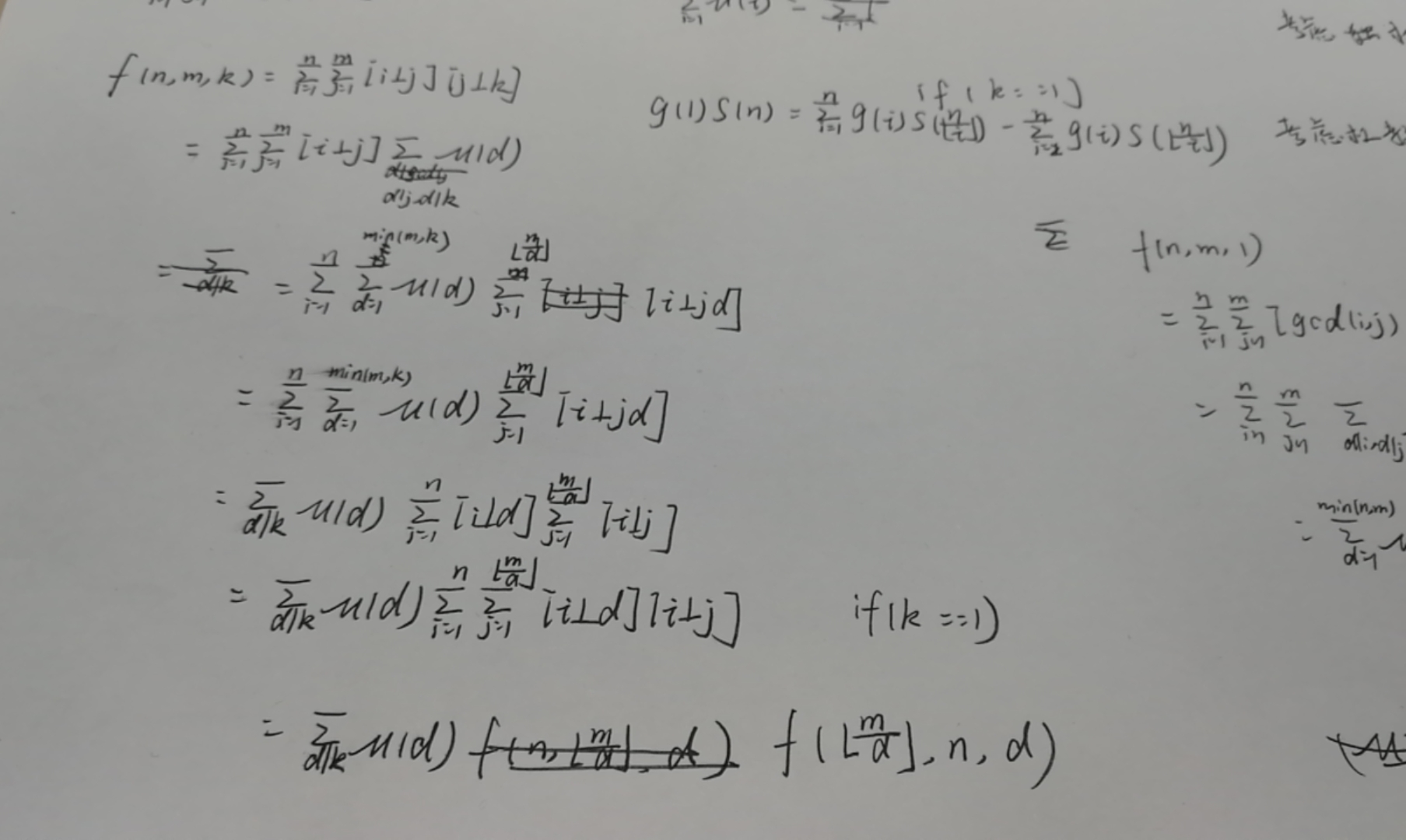
对于k = 1情况直接整除分块杜教筛即可
据说是ZJ神选2020的签到题,soulist大佬跟我说这是sb题
首先根据期望的线性性,可以对每个点分别考虑,最后再加起来即可
考虑这个点什么情况下可能打上标记
- 完全包含了这个区间且没有完全包含其父区间
- 父区间有标记,且修改到其兄弟,下传到它
考虑什么情况下打上的标记会被下传,显然是该点代表的区间被分割开来
可以发现我们除了关心某一轮该点是否有标记外,我们还关心其祖先是否有标记,考虑如下的状态设计,(以下都只讨论u一个节点)
- $g_i$表示第i轮,u节点有标记的概率
- $f_i$表示第i轮,u节点及其祖先没有标记的概率
- $h_i$表示第i轮,u节点没有标记,其存在祖先有标记的概率
另外预处理几个辅助数组
- $p1_u$表示u上一轮已有标记,这一轮不下传的概率
- $p2_u$表示该轮修改能把标记打到u上的概率
- $p3_u$表示该轮修改完全包含了父亲所在区间的概率
- $p4_u$表示该轮修改递归到u的兄弟,且没有修改到u的概率
- $p5_u$表示父亲标记没有下传的概率,显然$p5_u$ = $p1_{fa}$
特判1号节点,剩下的分类讨论转移,矩阵快速幂加速即可,具体看代码

#include<bits/stdc++.h> using namespace std; #define ll long long int read(){ char c = getchar(); int x = 0; while(c < '0' || c > '9') c = getchar(); while(c >= '0' && c <= '9') x = x * 10 + c - 48,c = getchar(); return x; } const int N = 1e6 + 10; #define mod 998244353 void add(int &x,int y){ x += y - mod; x += (x >> 31) & mod; } int p1[N],p2[N],p3[N],p4[N],p5[N],L[N],R[N],cnt,lc[N],rc[N],n,k; int qpow(int x,int y){ int ans = 1; while(y){ if(y & 1) ans = 1ll * ans * x % mod; x = 1ll * x * x % mod; y >>= 1; } return ans; } int C(int len){ return ((1ll * len * (len - 1) / 2) + len) % mod; } int Inv; void build(int &u,int fa,int l,int r,int tag){/*表示是左儿子还是右儿子*/ if(!u) u = ++cnt; L[u] = l,R[u] = r; int len = r - l + 1; if(u != 1){ int P = (1ll * (r - l) * (n - r + l - 1) + C(len) - 1) % mod; P = 1ll * P * Inv % mod; p1[u] = (1 - P + mod) % mod; int fal = L[fa],far = R[fa]; if(tag == 0){ p2[u] = 1ll * l * (far - r) * Inv % mod; p4[u] = 1ll * (1ll * (far - r) * (n - far) % mod + (C(far-r))) * Inv % mod; } else{ p2[u] = 1ll * (n - r + 1) * (l - fal) * Inv % mod; p4[u] = 1ll * (1ll * (l - fal) * (fal - 1) % mod + C(l - fal)) * Inv % mod; } p3[u] = 1ll * fal * (n - far + 1) % mod * Inv % mod; if(fa != 1) p5[u] = p1[fa]; else p5[u] = Inv; } if(l == r) return; int mid = read(); build(lc[u],u,l,mid,0); build(rc[u],u,mid+1,r,1); } int A[3][3],B[3][3],F[3],G[3]; void mul(){ memcpy(G,F,sizeof(F)); memset(F,0,sizeof(F)); for(int i = 0; i < 3; ++i) for(int j = 0; j < 3; ++j) add(F[i],1ll * A[i][j] * G[j] % mod); } void mulitself(){ memcpy(B,A,sizeof(A)); memset(A,0,sizeof(A)); for(int i = 0; i < 3; ++i) for(int j = 0; j < 3; ++j) for(int k = 0; k < 3; ++k) add(A[i][j],1ll * B[i][k] * B[k][j] % mod); } int calc(int u){ // clr(f);clr(g);clr(h); /*f[0] = 1; for(int i = 1; i <= k; ++i){ g[i] = (1ll * g[i-1] * p1[u] % mod + 1ll * (f[i-1] + h[i-1]) * p2[u] + 1ll * h[i-1] * p4[u]) % mod; h[i] = (1ll * f[i-1] * p3[u] % mod + 1ll * h[i-1] * p5[u]) % mod; f[i] = (1ll - g[i] - h[i] + 2ll * mod) % mod; } return g[k];*/ memset(F,0,sizeof(F)); F[2] = 1; A[0][0] = (p1[u] - p2[u] + mod) % mod,A[0][1] = p4[u],A[0][2] = p2[u]; A[1][0] = (mod - p3[u]) % mod,A[1][1] = (p5[u] - p3[u] + mod) % mod,A[1][2] = p3[u]; A[2][0] = 0,A[2][1] = 0,A[2][2] = 1; int m = k; while(m){ if(m & 1) mul(); mulitself(); m >>= 1; } return F[0]; } int main(){ int rt = 0;n = read(),k = read(); Inv = qpow(C(n),mod-2); build(rt,0,1,n,0); int ans = 0; for(int i = 2; i <= cnt; ++i) add(ans,calc(i)); add(ans,Inv); printf("%d\n",ans); return 0; }



