CF311E Biologist(最小割)
题目链接
CF:https://codeforc.es/contest/311/problem/E
luogu:https://www.luogu.com.cn/problem/CF311E
首先很套路地,我们可以先把所有的w[i]加起来,再考虑最小化代价
即Ans = Σw[i] - Mincut
我们可以把原来的字符串的点当作i(1 <= i <= n),m个要求也分别当作点i + n(1<= i <= m)
首先我们考虑一下限制条件:
1.如果不选这个要求,我们会损失w[i] 或 w[i] + g 设为f[i]
2.如果选了这个要求,以这个要求1为例,设这个要求需要为1的若干个位置为S,设原字符串数组为str[i],则满足i属于集合S且str[i] == 0的i都要改变,即付出v[i]的代价
3.相互矛盾的两个要求不能同时选,即某个要求需要位置i为0,另一个需要位置i为1,则这两个位置不能同时选
建模
1.我们考虑把str[i] == 1的点与S连边,流量为v[i],意即如果要变成0需要付出v[i]的代价,str[i] == 0则向T连边
2.我们考虑把要求1的点向S连边,流量为f[i],然后向它要求的点连边,流量为inf,为么
要这样连呢,因为这样连后我们会发现要么要把它向S的边割掉损失f[i],要么要把那些需要花代价变成1的点与T的连边割掉.意即要付出变成1需要花费的代价.要求0的点同理
然后我们就满足了要求1,2,然后交上去就AC了.
??????为什么???我们不是还没满足限制3吗?数据水????
这个地方是博主觉得这题最妙的地方,我们这样连边其实是满足限制3的
为什么呢,放一张图相信大家都能看懂
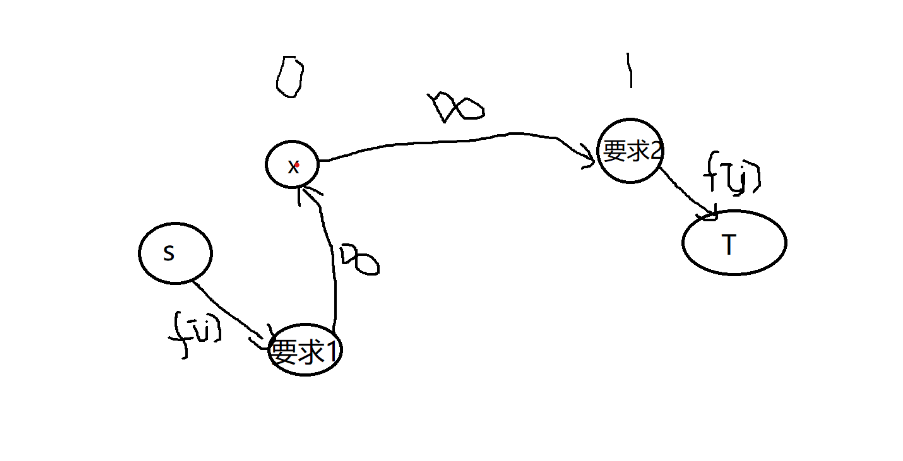
从图中可以看出要求1和要求2通过同一个点x形成了一条从S到T联通的路径,由于最小割要割断S和T的路径所以互相矛盾的要求不可能同时选
最优性可以由最小割算法本身保证
所以就做完这道题啦
代码如下
/*CF311E Biologist*/
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
#define ll long long
int read(){
char c = getchar();
int x = 0;
while(c < '0' || c > '9') c = getchar();
while(c >= '0' && c <= '9') x = x * 10 + c - 48,c = getchar();
return x;
}
const int maxn = 1e6 + 10;
struct Edge{
int nxt,point,flow;
}edge[maxn<<1];
int S,T,dep[maxn],cur[maxn],head[maxn],q[maxn],tot,n,m;
void add(int x,int y,int flow){
edge[++tot].nxt = head[x];edge[tot].point = y;edge[tot].flow = flow;head[x] = tot;
edge[++tot].nxt = head[y];edge[tot].point = x;edge[tot].flow = 0; head[y] = tot;
}
bool bfs(){
for(int i = S; i <= T; ++i) cur[i] = head[i],dep[i] = 0;
dep[S] = 1;
int l = 1,r = 0;
q[++r] = S;
while(l <= r){
int x = q[l++];
for(int i = head[x]; i ; i = edge[i].nxt){
int y = edge[i].point;
if(!dep[y] && edge[i].flow){
dep[y] = dep[x] + 1;
q[++r] = y;
}
}
}
return (dep[T] != 0);
}
int Dinic(int x,int flow){
if(x == T || !flow) return flow;
int rest = flow,k;
for(int i = cur[x]; i ; i = edge[i].nxt){
int y = edge[i].point;
cur[x] = i;
if(edge[i].flow && dep[y] == dep[x] + 1){
k = Dinic(y,min(edge[i].flow,rest));
if(!k) dep[y] = 0;
rest -= k;
edge[i].flow -= k;
edge[i^1].flow += k;
}
}
return flow - rest;
}
int v[maxn];
int str[maxn];
int main(){
tot = 1;
n = read(),m = read();int g = read();
T = n + m + 1;
for(int i = 1; i <= n; ++i) str[i] = read();
for(int i = 1; i <= n; ++i){
v[i] = read();
if(str[i] == 1) add(S,i,v[i]);
else add(i,T,v[i]);
}
ll ans = 0;
for(int i = 1; i <= m; ++i){
int opt = read();int w = read(),k = read();
ans += w;
for(int j = 1; j <= k; ++j){
int x = read();
if(opt) add(n+i,x,1e9);
else add(x,n+i,1e9);
}
int t = read();
if(opt) add(S,n+i,w+g*t);
else add(n+i,T,w+g*t);
}
while(bfs()) ans -= Dinic(S,1e9);
cout<<ans<<endl;
return 0;
}


