WC2016 Fountain(计数DP)

题意:

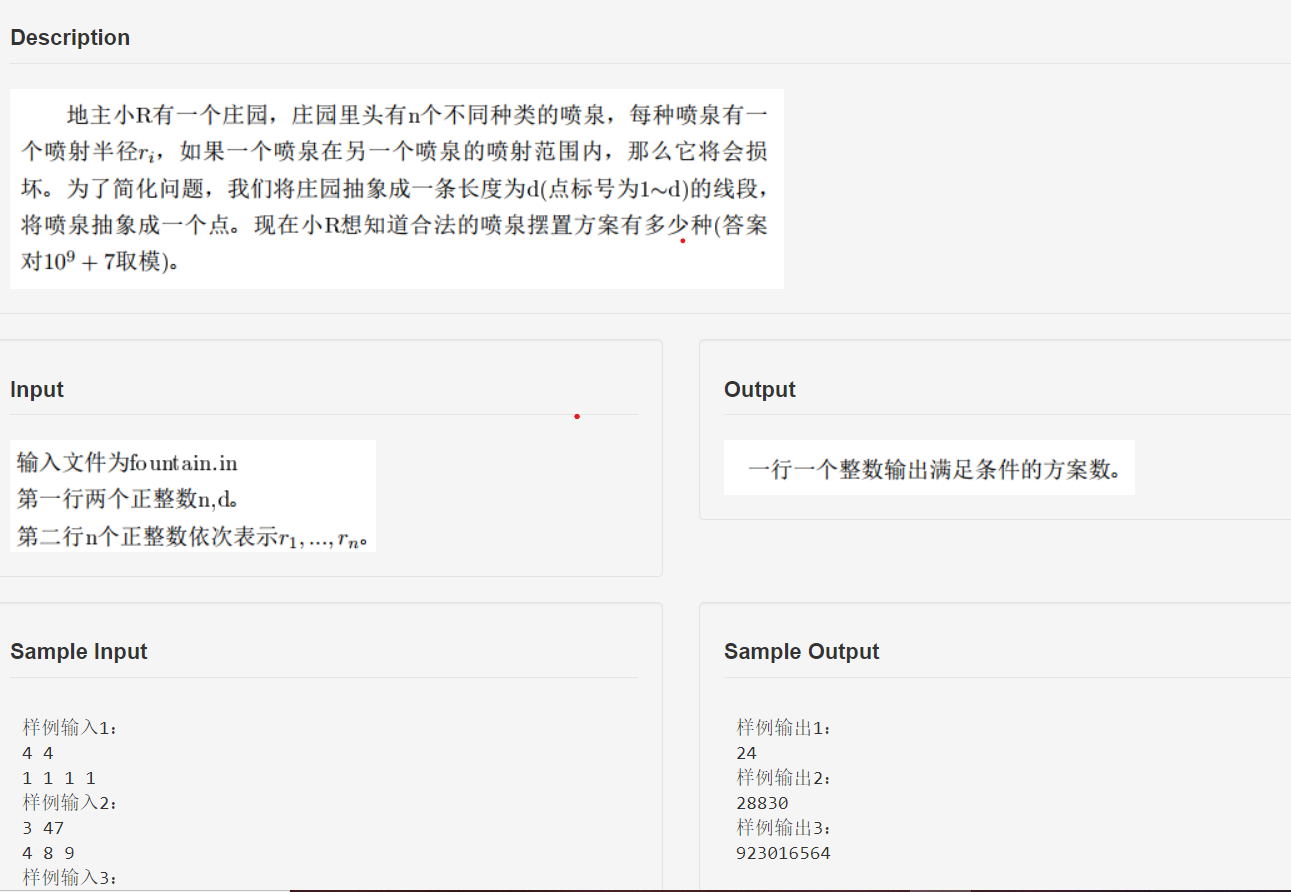
数据范围:n <= 40,r_i <= 40,d = 1e5

解析:首先我们可以发现对于一个确定的排列,{p₁……p_n}令D = Σmax(r_pi,r_pi+1) ,即放这n个喷泉对于该排列所需得最小空间,方案数就是C(n + d - 1 - D,n);

所以我们可以对于每个D计算方案数,怎么做?DP!不过DP面临这几个问题,首先没有顺序,于是我们可以将r数组先排序,然后从小到大插进去,这样就有序了,为什么要从小到大?这样保证r插进去一定是max取的那个,即让r对D作贡献,方便计算.第二个问题,假设我们设dp[i][j]为计算到第i个数,当前d值为j,我们会发现极其难以计算.分析发现,一个值插进去只有三种情况,要么做r[i]的贡献,要么做2*r[i]的贡献,要么不做贡献

于是我们可以想到dp的一个奇迹淫巧:计算贡献而非当前值,或叫费用延后计算(其实跟费用提前计算是一个思想)
然后我们注意到,如果一个值插进去明明可以作贡献却没做贡献,那一定是留了一个空给后面的值作贡献

于是我们可以定义:dp[i][j][k]为计算到第i个数,当前对d的贡献为j(注意是贡献,而不是当前d值,和前面不一样),留了k个空的方案

于是显然有以下dp转移方程:

dp[i+1][j][k+1] = (k + 2) * dp[i][j][k] + dp[i+1][j][k+1]
dp[i+1][j+r[i+1]][k] = (2 * k + 2) * dp[i][j][k] + dp[i+1][j+r[i+1]][k]
if(k)
　　dp[i+1][j+2*r[i+1]][k-1] = k * dp[i][j][k] + dp[i+1][j+2*r[i+1]][k-1]

加2是因为首尾也可以插空或者作贡献,k*2是因为插的空可以是左边也可以是右边

dp转移方程就不细说了,如果理解了前面的思想应该很好推出(其实是我懒了)

代码如下:

/*fountain*/ 
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
#define ll long long
const int maxn = 41;
const int maxm = 2005;
int dp[maxn][maxm][maxn];
int jc[200010],invjc[200010];
const int mod = 1e9 + 7;
int qpow(int x,int y){
	int ans = 1;
	while(y){
		if(y & 1)	ans = 1ll * ans * x % mod;
		x = 1ll * x * x % mod;
		y >>= 1;
	}
	return ans;
}
int read(){
	char c = getchar();
	int x = 0;
	while(c < '0' || c > '9')	c = getchar();
	while(c >= '0' && c <= '9')		x = x * 10 + c - 48,c = getchar();
	return x;
}
int r[maxn];
int C(int x,int y){
	return 1ll * jc[x] * invjc[y] % mod * invjc[x-y] % mod;
}
int main()
{
	jc[0] = invjc[0] = 1;
	for(int i = 1; i <= 2e5; ++i)
		jc[i] = 1ll * jc[i-1] * i % mod,invjc[i] = qpow(jc[i],mod-2);
	dp[1][0][0] = 1;
	int n = read(),d = read();
	for(int i = 1; i <= n; ++i)
		r[i] = read();
	sort(r+1,r+n+1);
	for(int i = 1; i < n; ++i){
		for(int k = 0; k < i; ++k){
			for(int j = 0; j <= 1600; ++j){
				if(!dp[i][j][k])	continue;
				dp[i+1][j][k+1] = (1ll * (k + 2) * dp[i][j][k] + dp[i+1][j][k+1]) % mod;
				dp[i+1][j+r[i+1]][k] = (1ll * (2 * k + 2) * dp[i][j][k] + dp[i+1][j+r[i+1]][k]) % mod;
				if(k)
					dp[i+1][j+2*r[i+1]][k-1] = (1ll * k * dp[i][j][k] + dp[i+1][j+2*r[i+1]][k-1]) % mod;
			}
		}
	}
	int ans = 0;
	for(int i = 0; i < min(d,1601); ++i){
		ans = (1ll * C(d - i - 1 + n,n) * dp[n][i][0] + ans) % mod; 
	}
	printf("%d\n",ans);
	return 0;
}