一、前言
1.知识点:
(1)第四次题目集:共有三道题,考察内容主要为正则表达式的运用,还有字符串的提取,数据的查找,还有第三题银行业务类的设计,以及四边形的设计。
(2)期中考试题目集:共有三道题,第三题原型与第一、二题的基础,并加强难度,改变代码,在“点与线(继承与多态)”题目基础上,增加容器类保存点、线、面对象,并对该容器进行相应增、删、遍历操作。此题的难度在于如何建立容器,在容器中建立各个对象,主要考察我们继承与多态,此题难度高于前两道题,略显困难。
(3)第五次题目集:只有两道题,但难度较大,从点类到线类再到形类,不仅考察了我们数学知识,更让我们更深入体会到了类与对象的关系,并且在理解题目含义的同时运用类的创建(包含 若干属性和若干方法)以及多个类的创建来完成整个代码的框架与思路。
2.题量与难度:
(1)、 本次题目共分为三次练习题,分别考察判断、循环、数组的建立、运用,加强了我对数组中数据的应用、查找、判断。
(2)、题目集一的难度相对比较简单一些,非是困难程度,题目集一是侧重于对基础知识点的掌握,加强了我的java基础。加强了我对调用数据的应用,学会了如何在文字中提出数字,并进行计算,排序。坐标的输入,读取,计算,判断最终出值与输出的关系。学会(静态、公有方法),存款,取款等操作。
(3)、还有期中考试三道题目从类的设计到继承再到容器地一系列题目,学会了建立多类,本次3题的难度大于题目集一题目的难度,其中知识的考查包括题目集一知识,多些为数组中转化的运用,指定数组输出,判断指定输出,内容判断,内容提取等等,练习程序多种运用写法,加强运用性,本次题目集的重点为第二题,本题目的难度略大于其他题目难度,起初并不知道如何去写,在书上学习和上网查询后也掌握了后了解怎样进行编程,考察了我们对于字符串数组,以及字符串.length()方法的用法,相对简单,本次题目加强了我对java的多方面运用,对java用法更灵活。
二、设计与分析
7-1 sdut-String-2 识蛟龙号载人深潜,立科技报国志(II)(正则表达式)
import java.util.Scanner; import java.util.Arrays; public class Main{ public static void main(String[] args){ Scanner sc=new Scanner(System.in); while(true){ String line=sc.nextLine(); if(line.equals("end")) break; String[] split=line.split("\\D+"); int n; long sum=0; for(n=0;n<split.length;n++){ if(!split[n].equals("")) { int digit=Integer.parseInt(split[n]); sum+=digit; } } System.out.println(sum); } } }
解释与心得:
该题主要考察正则表达式的运用,主考察我们文字中提取数字,并进行运算,其中主要运用正则表达式,通过本次题目我了解并学会了正则表达式,正则表达式是解决此题的关键,依赖性也较大,使类与类之间的联系更紧切,此题大部分运用数组并对数组中数据的查找,数组的储存中字符串的调用,输出等等。
7-3 设计一个银行业务类
类图如下: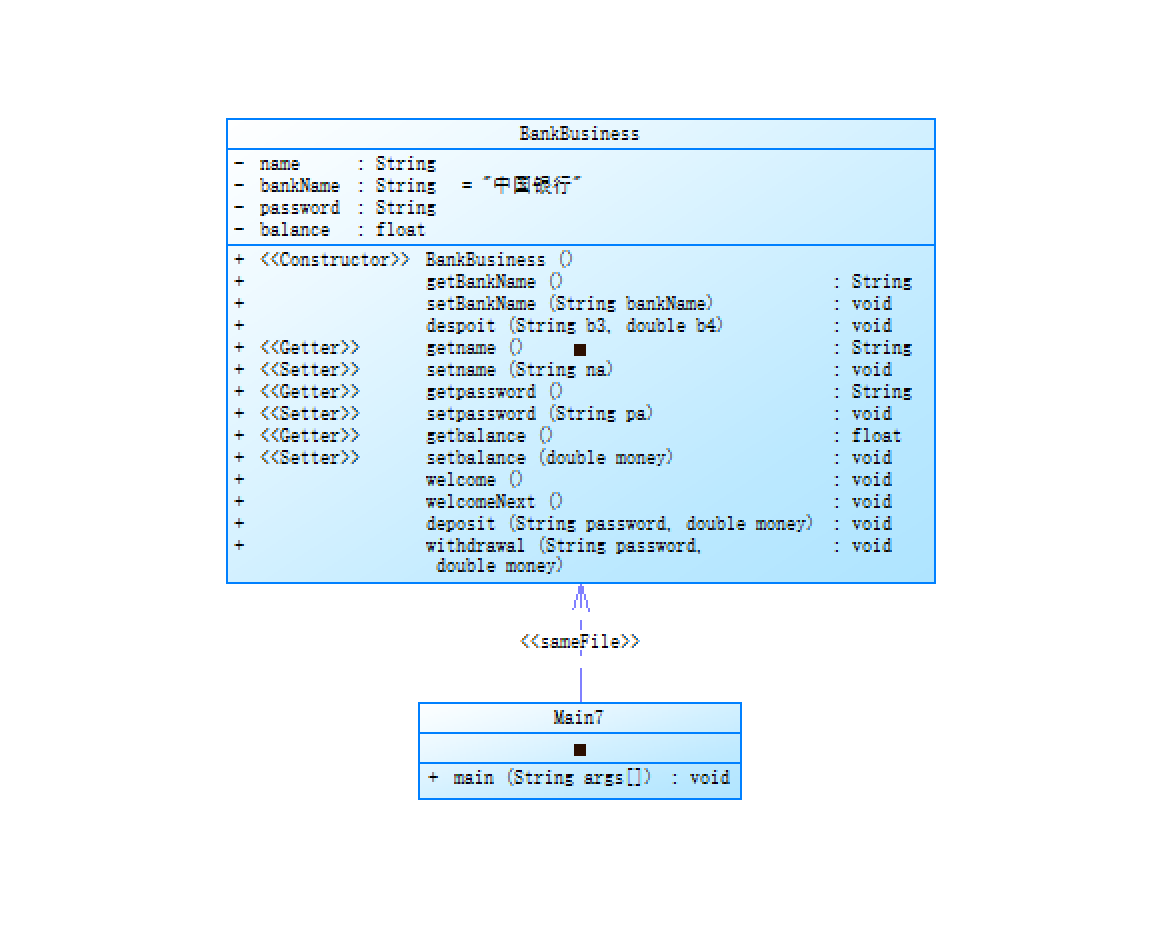
import java.util.Scanner; public class Main{ public static void main(String[] args) { // TODO Auto-generated method stub BankBusiness bank = new BankBusiness(); bank.welcome(); Scanner in = new Scanner(System.in); String b1=in.next(); String b2=in.next(); BankBusiness account= new BankBusiness(); String b3=in.next(); double b4=in.nextDouble(); account.despoit(b3,b4); String b5=in.next(); double b6=in.nextDouble(); account.withdrawal(b5,b6); String b7=in.next(); double b8=in.nextDouble(); account.withdrawal(b7, b8); String b9=in.next(); double b10 =in.nextDouble(); account.withdrawal(b9,b10); BankBusiness next=new BankBusiness(); bank.welcomeNext(); } }
class BankBusiness {
public static String bankName = "中国银行";
private String name,password;
private double balance;
public static void welcome() {
System.out.println(bankName+"欢迎您的到来!");
}
public static void welcomeNext() {
System.out.println("请收好您的证件和物品,欢迎您下次光临!");
}
public BankBusiness(String name, String password) {
super();
this.name = name;
this.password = password;
this.balance = 0;
}
public void deposit(String password,double change) {
if(!password.equals(this.password)) {
System.out.println("您的密码错误!");
return;
}
this.balance += change;
System.out.println("您的余额有"+this.balance+"元。");
}
public void withdraw(String password,double change) {
if(!password.equals(this.password)) {
System.out.println("您的密码错误!");
return;
}
if(this.balance<change) {
System.out.println("您的余额不足!");
return;
}
this.balance -= change;
System.out.println("请取走钞票,您的余额还有"+this.balance+"元。");
}
}
解释与心得:我觉得本题的难点主要在于如何读取到我们所要输入的几行代码。并且能够正确地利用。最初在这里卡了很久。
第三次作业:7-1点线形系列5-凸五边形的计算-1
import java.text.DecimalFormat; // import java.util.ArrayList; import java.util.Arrays; import java.util.Scanner; import java.util.ArrayList; //用于格式化存储用户输入的数据。 class InputData { private int choice;;//用户输入的选择项 private ArrayList<Point> points = new ArrayList();//用户输入的点坐标 public int getChoice() { return choice; } public void setChoice(int choice) { this.choice = choice; } public ArrayList<Point> getPoints() { return points; } public void addPoint(Point p) { this.points.add(p); } } class Line { private Point p1;//线上的第一个点 private Point p2;//线上的第二个点 public Line(double x1, double y1, double x2, double y2) { Point p1 = new Point(x1, y1); Point p2 = new Point(x2, y2); LineInputError.pointsCoincideError(p1, p2);//两点是否重合,重合则报错并退出 this.p1 = p1; this.p2 = p2; } public Line(Point p1, Point p2) { LineInputError.pointsCoincideError(p1, p2);//两点是否重合,重合则报错并退出 this.p1 = p1; this.p2 = p2; } /* 获取线条的斜率 */ public Double getSlope() { // (x1-x2=0)注意考虑斜率不存在即返回double类型无穷大"Infinite" return (p2.getY() - p1.getY()) / (p2.getX() - p1.getX()); } /* 判断x是否在线上 */ public boolean isOnline(Point x) { //System.out.println("isOnline"); //System.out.println(p1.x + " " + p1.y + " " + p2.x + " " + p2.y + " " + x.x + " " + x.y + " "); // 点重合 if ((x.getX() == p1.getX() && x.getY() == p1.getY()) || (x.getX() == p2.getX() && x.getY() == p2.getY())) { return true; } Line l = new Line(p1, x); if (l.getSlope().isInfinite() && this.getSlope().isInfinite()) { return true; } /* * if (l.getSlope().isInfinite() || this.getSlope().isInfinite()) { return * false; } */ // 此点与线上任意一点构成的线的斜率相等则此点在线上 double b1 = l.getSlope(), b2 = this.getSlope(); //System.out.println(b1 + " " + b2 + " " + (b1- b2) + " " + (Math.abs(b1 - b2) < 0.00000000001)); return Math.abs(b1 - b2) < 0.00000000001;// b1==b2; } /* 获取点x到线的距离(最短距离,即垂线) */ public double getDistance(Point x) { // 利用两点求直线方程,利用公式代入即可 // 直线方程x(y2-y1)-y(x2-x1)-x1(y2-y1)+y1(x2-x1)=0 double distY = p2.getY() - p1.getY(); double distX = p2.getX() - p1.getX(); return Math.abs(x.getX() * distY - x.getY() * distX - p1.getX() * distY + p1.getY() * distX) / p1.getDistance(p2); } /* 判断x是否在线上且在两点之间 */ public boolean isBetween(Point x) { //System.out.println("isBetween" + " " + this.p1.x + " " + p1.y + " " + p2.x + " " + p2.y + " " + x.x + " " + x.y); if (!this.isOnline(x)) { return false; } // 与端点重合,认为不在在两点之间, if (x.equals(p1) || x.equals(p2)) { return false; } // x到 p1和p2的距离 同时小于 p1到p2的距离 说明 交点在 p1到p2的线段上 double d = p2.getDistance(p1); boolean b = x.getDistance(p2) < d && x.getDistance(p1) < d; //System.out.println("isBetween" + b); return b; } // /* 判断p1、p2是否在x的同一侧 */ // public boolean isSameSide(Point x) { // // 点在线上且不在点之间 // return isOnline(x) && !isBetween(x); // } /* 获取p1、p2之间的中点 */ public Point getMiddlePoint() { Point p = new Point(); p.setX((p1.getX() + p2.getX()) / 2); p.setY((p1.getY() + p2.getY()) / 2); return p; } /* 获取线段的第一个坐标点 */ public Point getPointA() { return p1; } /* 获取线段的第二个坐标点 */ public Point getPointB() { return p2; } /* 获取与线条l之间的夹角,若两条线段交叉(交叉点位于其中一条线的两点之间),取较小的夹角 */ public double getAngle(Line l) { // 利用公式θ=arctan∣(k2- k1)/(1+ k1k2)∣,此时求较小的夹角 double k2 = getSlope(); double k1 = l.getSlope(); return (double) (Math.atan(Math.abs((k2 - k1) / (1 + k1 * k2))) * 180.0 / Math.PI);// 返回值为角度 } // 是否平行,平行返回true,否则false。 public boolean isParallel(Line l) { Double b1 = this.getSlope(); Double b2 = l.getSlope(); if ((b1.isInfinite()) && (b2.isInfinite())) { return true; } else { return (this.getSlope().doubleValue() == l.getSlope().doubleValue()); } } // 两条线是否重合,重合返回true,否则false。 public boolean isCoincide(Line l) { if (!this.isParallel(l)) { return false; } if (this.isOnline(l.p1)) { return true; } return false; } // 获取交叉点,若两条线平行,返回null。 public Point getIntersection(Line l) { // LineInputError.isParallelError(this, l); if (this.isParallel(l)) { return null; } if (p1.equals(l.p1) || p1.equals(l.p2)) { return p1; } if (p2.equals(l.p1) || p2.equals(l.p2)) { return p2; } Point p3 = l.p1, p4 = l.p2; double x_member, x_denominator, y_member, y_denominator; Point cross_point = new Point(); x_denominator = p4.x * p2.y - p4.x * p1.y - p3.x * p2.y + p3.x * p1.y - p2.x * p4.y + p2.x * p3.y + p1.x * p4.y - p1.x * p3.y; x_member = p3.y * p4.x * p2.x - p4.y * p3.x * p2.x - p3.y * p4.x * p1.x + p4.y * p3.x * p1.x - p1.y * p2.x * p4.x + p2.y * p1.x * p4.x + p1.y * p2.x * p3.x - p2.y * p1.x * p3.x; if (x_denominator == 0) cross_point.x = 0; else cross_point.x = x_member / x_denominator; y_denominator = p4.y * p2.x - p4.y * p1.x - p3.y * p2.x + p1.x * p3.y - p2.y * p4.x + p2.y * p3.x + p1.y * p4.x - p1.y * p3.x; y_member = -p3.y * p4.x * p2.y + p4.y * p3.x * p2.y + p3.y * p4.x * p1.y - p4.y * p3.x * p1.y + p1.y * p2.x * p4.y - p1.y * p2.x * p3.y - p2.y * p1.x * p4.y + p2.y * p1.x * p3.y; if (y_denominator == 0) cross_point.y = 0; else cross_point.y = y_member / y_denominator; // System.out.println(cross_point.x + ","+cross_point.y); return cross_point; // 平行返回(0,0) } } class LineInputError { // 直线的两点重合的错误判断和提示。 public static void pointsCoincideError(Point p1, Point p2) { if ((p1.getX() == p2.getX()) && p1.getY() == p2.getY()) { System.out.println("points coincide"); System.exit(0); } } } public class Main { public static void main(String[] args) { Scanner in = new Scanner(System.in); String s = in.nextLine(); InputData d = new InputData(); ParseInput.paseInput(s, d); int choice = d.getChoice(); ArrayList ps = d.getPoints(); switch (choice) { case 1: handle1(ps,s); break; case 2: handle2(ps); break; case 3: handle3(ps); break; // case 4: // handle4(ps); // break; // case 5: // handle5(ps); // break; // case 6: // handle6(ps); // break; } } // 输入五个点坐标,判断是否是五边形 public static void handle1(ArrayList<Point> ps,String s) { PointInputError.wrongNumberOfPoints(ps, 5); pentagon t = new pentagon(ps.get(0), ps.get(1), ps.get(2),ps.get(3),ps.get(4)); System.out.println(t.isPentagon()); } // 输入五个点坐标,输出周长、面积。 public static void handle2(ArrayList<Point> ps) { PointInputError.wrongNumberOfPoints(ps, 5); pentagon t = new pentagon(ps.get(0), ps.get(1), ps.get(2),ps.get(3),ps.get(4)); if(t.isPentagon()==false) { System.out.println("not a pentagon"); System.exit(0); } else { if(t.judge1()==true) { System.out.print(t.judge1()); double d = t.length(); double s=t.S(); System.out.println(" "+OutFormat.doubleFormat(d) + " " + OutFormat.doubleFormat(s)); } else { System.out.println("false"); } } } // 输入七个点坐标,计算面积 public static void handle3(ArrayList<Point> ps) { PointInputError.wrongNumberOfPoints(ps, 7); Line l=new Line(ps.get(0),ps.get(1)); pentagon t = new pentagon(ps.get(2),ps.get(3),ps.get(4),ps.get(5),ps.get(6)); if(t.judgeLineCoincide(l)) { System.out.println("The line is coincide with one of the lines"); System.exit(0); } else if(ps.get(0).equals(ps.get(1))) { System.out.println("points coincide"); System.exit(0); } int num=t.Num(l); if(num==2) { double[] ds = {t.areaFive(l),t.areaFive1(l)}; Arrays.sort(ds); System.out.println(num + " " + OutFormat.doubleFormat(ds[0]) + " " + OutFormat.doubleFormat(ds[1])); } else { System.out.println(num); } class OutFormat { //按要求格式化实数的输出。 public static Double doubleFormat(double b) { DecimalFormat df = new DecimalFormat("#.000"); Double output = Double.valueOf(df.format(b)); return output; } } class ParseInput { /* * 输入:完整的输入字符串,包含选项和所有点的信息,格式:选项:x1,y1 x2,y2 .....xn,yn。选项只能是1-5 * 一个空InputData对象 * 处理:将输入字符串中的选项和点信息提取出来并设置到InputData对象中 * 输出:包含选项值和所有点的Point对象的InputData对象。 */ public static void paseInput(String s, InputData d) { PointInputError.wrongChoice(s); d.setChoice(getChoice(s)); s = s.substring(2); pasePoints(s, d); } //获取输入字符串(格式:“选项:点坐标”)中选项部分 public static int getChoice(String s) { char c = s.charAt(0); return c-48; } /* * 输入:一个字符串,包含所有点的信息,格式:x1,y1 x2,y2 .....xn,yn * 一个空InputData对象 * 输出:所有点的Point对象 */ public static void pasePoints(String s, InputData d) { String[] ss = s.split(" "); if (ss.length == 0) return; for (int i = 0; i < ss.length; i++) { d.addPoint(readPoint(ss[i])); } } /* * 输入:包含单个点信息的字符串,格式:x,y * 输出:Point对象 */ public static Point readPoint(String s) { PointInputError.wrongPointFormat(s); String[] ss = s.split(","); double x = Double.parseDouble(ss[0]); double y = Double.parseDouble(ss[1]); // System.out.println("match"); return new Point(x, y); } } class pentagon { private Point a; private Point b; private Point c; private Point d; private Point e; public pentagon(Point a, Point b, Point c, Point d, Point e) { this.a = a; this.b = b; this.c = c; this.d = d; this.e = e; // if (!this.isPentagon()) { // System.out.println("not a pentagon"); // System.exit(0); // } } /* 判断a\b\c\d\e五个点的坐标是否能构成一个五边形 */ public boolean isPentagon() { double slope1=0; double slope2=0; double slope3=0; double slope4=0; double slope5=0; double slope6=0; Point p=new Point(); int t=0; if((this.a.getX()==this.b.getX()&&this.b.getX()==this.c.getX())||(this.b.getX()==this.c.getX()&&this.c.getX()==this.d.getX())||(this.c.getX()==this.d.getX()&&this.d.getX()==this.e.getX())||(this.d.getX()==this.e.getX()&&this.a.getX()==this.e.getX())) { t=1; } else if(t==0){ slope1=Slope(this.a.getX(),this.b.getX(),this.a.getY(),this.b.getY()); slope2=Slope(this.b.getX(),this.c.getX(),this.b.getY(),this.c.getY()); slope3=Slope(this.c.getX(),this.d.getX(),this.c.getY(),this.d.getY()); slope4=Slope(this.d.getX(),this.e.getX(),this.d.getY(),this.e.getY()); slope5=Slope(this.e.getX(),this.a.getX(),this.e.getY(),this.a.getY()); } if(slope1==slope2||slope2==slope3||slope3==slope4||slope4==slope5||t==1|| judge(this.a.getX(),this.a.getY(),this.b.getX(),this.b.getY(),this.c.getX(),this.c.getY(),this.d.getX(),this.d.getY()) ||judge(this.a.getX(),this.a.getY(),this.b.getX(),this.b.getY(),this.e.getX(),this.e.getY(),this.d.getX(),this.d.getY()) ||judge(this.c.getX(),this.c.getY(),this.b.getX(),this.b.getY(),this.e.getX(),this.e.getY(),this.d.getX(),this.d.getY()) ||judge(this.c.getX(),this.c.getY(),this.b.getX(),this.b.getY(),this.e.getX(),this.e.getY(),this.a.getX(),this.a.getY()) ||judge(this.c.getX(),this.c.getY(),this.d.getX(),this.d.getY(),this.e.getX(),this.e.getY(),this.a.getX(),this.a.getY())) { return false; } else { return true; } } /*计算两点斜率*/ public double Slope(double x1,double x2,double y1,double y2) { double slope=(y2-y1)/(x2-x1); return slope; } public boolean judge(double Ax1,double Ay1,double Ax2,double Ay2,double Bx1,double By1,double Bx2,double By2) { if(java.awt.geom.Line2D.linesIntersect(Ax1, Ay1, Ax2, Ay2, Bx1, By2, Bx2,By2)) { return true; } else { return false; } } //三角形面积 public double TriangleS(double x1,double y1,double x2,double y2,double x3,double y3) { double a=line(x1,y1,x2,y2); double b=line(x1,y1,x3,y3); double c=line(x2,y2,x3,y3); double p=(a+b+c)/2; double s=Math.sqrt(p*(p-a)*(p-b)*(p-c)); return s; } //判断是凹五边形还是凸五边形 public boolean judge1() { double s1=TriangleS(this.a.getX(),this.a.getY(),this.b.getX(),this.b.getY(),this.c.getX(),this.c.getY())+ TriangleS(this.a.getX(),this.a.getY(),this.c.getX(),this.c.getY(),this.d.getX(),this.d.getY())+ TriangleS(this.a.getX(),this.a.getY(),this.d.getX(),this.d.getY(),this.e.getX(),this.e.getY()); double s2=TriangleS(this.a.getX(),this.a.getY(),this.b.getX(),this.b.getY(),this.d.getX(),this.d.getY())+ TriangleS(this.b.getX(),this.b.getY(),this.c.getX(),this.c.getY(),this.d.getX(),this.d.getY())+ TriangleS(this.a.getX(),this.a.getY(),this.d.getX(),this.d.getY(),this.e.getX(),this.e.getY()); if(Math.abs(s1-s2)<0.000000000000001) { return true; } else { return false; } } //五边形周长 public double length() { double length1=line(this.a.getX(),this.a.getY(),this.b.getX(),this.b.getY()); double length2=line(this.b.getX(),this.b.getY(),this.c.getX(),this.c.getY()); double length3=line(this.c.getX(),this.c.getY(),this.d.getX(),this.d.getY()); double length4=line(this.d.getX(),this.d.getY(),this.e.getX(),this.e.getY()); double length5=line(this.a.getX(),this.a.getY(),this.e.getX(),this.e.getY()); double length=length1+length2+length3+length4+length5; return length; } //每条边边长 public double line(double x1,double y1,double x2,double y2) { double line=Math.sqrt(Math.pow(x2-x1, 2)+Math.pow(y2-y1,2)); return line; } //五边形面积 public double S() { double s1=TriangleS(this.a.getX(),this.a.getY(),this.b.getX(),this.b.getY(),this.c.getX(),this.c.getY())+ TriangleS(this.a.getX(),this.a.getY(),this.c.getX(),this.c.getY(),this.d.getX(),this.d.getY())+ TriangleS(this.a.getX(),this.a.getY(),this.d.getX(),this.d.getY(),this.e.getX(),this.e.getY()); return s1; } // 判断线是否与五边形的某条边重合 public boolean judgeLineCoincide(Line l) { Line line1=new Line(this.a.getX(),this.a.getY(),this.b.getX(),this.b.getY()); Line line2=new Line(this.b.getX(),this.b.getY(),this.c.getX(),this.c.getY()); Line line3=new Line(this.c.getX(),this.c.getY(),this.d.getX(),this.d.getY()); Line line4=new Line(this.d.getX(),this.d.getY(),this.e.getX(),this.e.getY()); Line line5=new Line(this.e.getX(),this.e.getY(),this.a.getX(),this.a.getY()); if(line1.isCoincide(l)||line2.isCoincide(l)||line3.isCoincide(l)||line4.isCoincide(l)||line5.isCoincide(l)) { return true; } else { return false; } } //判断是否为四边形 public boolean judgefour(Line l) { if(a.equals(b)||a.equals(c)||a.equals(d)||a.equals(e)||b.equals(c)||b.equals(d)||b.equals(e)||c.equals(d)||c.equals(e)||d.equals(e)) { return true; } else if(!isPentagon()) { return true; } else { return false; } } //判断是否为三角形 public boolean judgethree() { int count=0; double[] slope=new double[5]; int t=0; if((this.a.getX()==this.b.getX()&&this.b.getX()==this.c.getX())||(this.b.getX()==this.c.getX()&&this.c.getX()==this.d.getX())||(this.c.getX()==this.d.getX()&&this.d.getX()==this.e.getX())||(this.d.getX()==this.e.getX()&&this.a.getX()==this.e.getX())) { t=1; } else if(t==1) { slope[0]=Slope(this.a.getX(),this.b.getX(),this.a.getY(),this.b.getY()); slope[1]=Slope(this.b.getX(),this.c.getX(),this.b.getY(),this.c.getY()); slope[2]=Slope(this.c.getX(),this.d.getX(),this.c.getY(),this.d.getY()); slope[3]=Slope(this.d.getX(),this.e.getX(),this.d.getY(),this.e.getY()); slope[4]=Slope(this.e.getX(),this.a.getX(),this.e.getY(),this.a.getY()); for(int i=0;i<5;i++) { if(slope[i]==slope[i+1]||slope[4]==slope[0]) { count++; } } } if(count==2) { return true; } else if((a.equals(b)&&a.equals(c))||(a.equals(b)&&a.equals(d))||(a.equals(b)&&a.equals(e))||(a.equals(c)&&a.equals(d))||(a.equals(c)&&a.equals(e))||(a.equals(d)&&a.equals(e))||(b.equals(c)&&b.equals(d))||(b.equals(c)&&b.equals(e))||(b.equals(d)&&b.equals(e))||(c.equals(d)&&c.equals(e))) { return true; } else { return false; } } /* * 输入:点p * 输出:p是否在本五边形的五条边线(不含顶点)上。在线上输出true,否则输出false。 */ public boolean isOnTheEdge(Point p) { Line a6=new Line(a,b); Line a7=new Line(b,c); Line a8=new Line(c,d); Line a9=new Line(d,e); Line a10=new Line(e,a); if(a6.isOnline(p)||a7.isOnline(p)||a8.isOnline(p)||a9.isOnline(p)||a10.isOnline(p)) { return true; } else { return false; } } //计算交点 public Point getIntersection(Point p1, Point p2, Point p3, Point p4) { double A1=p1.getY()-p2.getY(); double B1=p2.getX()-p1.getX(); double C1=A1*p1.getX()+B1*p1.getY(); double A2=p3.getY()-p4.getY(); double B2=p4.getX()-p3.getX(); double C2=A2*p3.getX()+B2*p3.getY(); double det_k=A1*B2-A2*B1; if(Math.abs(det_k)<0.00001){ return null; } double a=B2/det_k; double b=-1*B1/det_k; double c=-1*A2/det_k; double d=A1/det_k; double x=a*C1+b*C2; double y=c*C1+d*C2; return new Point(x,y); } //点在线段上 public boolean onsegment(Point pi,Point pj,Point Q) { if((Q.x-pi.x)*(pj.y-pi.y)==(pj.x-pi.x)*(Q.y-pi.y)&&min(pi.x,pj.x)<Q.x&&Q.x<max(pi.x,pj.x)&&min(pi.y,pj.y)<Q.y&&Q.y<max(pi.y,pj.y)){ return true; }else{ return false; } } public double min(double x,double y) { if(x<y) { return x; } if(x>=y) { x=y; } return x; } public double max(double x,double y) { if(x>y) { return x; } if(x<=y) { x=y; } return x; } //计算线与五边形有几条交点 public int Num(Line l) { double num=0; if(getIntersection(a,b,l.getPointA(),l.getPointB()) != null&&onsegment(a,b,getIntersection(a,b,l.getPointA(),l.getPointB())) ) { num++; } if(getIntersection(b,c,l.getPointA(),l.getPointB()) != null&&onsegment(b,c,getIntersection(b,c,l.getPointA(),l.getPointB()))) { num++; } if(getIntersection(c,d,l.getPointA(),l.getPointB()) != null&&onsegment(c,d,getIntersection(c,d,l.getPointA(),l.getPointB())) ) { num++; } if(getIntersection(d,e,l.getPointA(),l.getPointB()) != null&&onsegment(d,e,getIntersection(d,e,l.getPointA(),l.getPointB())) ) { num++; } if(getIntersection(e,a,l.getPointA(),l.getPointB()) != null&&onsegment(e,a,getIntersection(e,a,l.getPointA(),l.getPointB())) ) { num++; } if(getIntersection(a,b,l.getPointA(),l.getPointB()) != null&&(getIntersection(a,b, l.getPointA(),l.getPointB()).equals(a)||getIntersection(a,b, l.getPointA(),l.getPointB()).equals(b))){ num=num+0.5; } if(getIntersection(b,c,l.getPointA(),l.getPointB()) != null&&(getIntersection(b,c, l.getPointA(),l.getPointB()).equals(b)||getIntersection(b,c, l.getPointA(),l.getPointB()).equals(c))){ num=num+0.5; } if(getIntersection(c,d,l.getPointA(),l.getPointB()) != null&&(getIntersection(c,d, l.getPointA(),l.getPointB()).equals(c)||getIntersection(c,d, l.getPointA(),l.getPointB()).equals(d))){ num=num+0.5; } if(getIntersection(d,e,l.getPointA(),l.getPointB()) != null&&(getIntersection(d,e, l.getPointA(),l.getPointB()).equals(d)||getIntersection(d,e, l.getPointA(),l.getPointB()).equals(e))){ num=num+0.5; } if(getIntersection(e,a,l.getPointA(),l.getPointB()) != null&&(getIntersection(e,a, l.getPointA(),l.getPointB()).equals(e)||getIntersection(e,a, l.getPointA(),l.getPointB()).equals(a))){ num=num+0.5; } return (int) num; } //判断点是否为五边形的顶点 public boolean isOnPeak(Point p) { if(p.equals(a)||p.equals(b)||p.equals(c)||p.equals(d)||p.equals(e)) { return true; } else { return false; } } //求直线穿过五边形的两部分面积 public double areaFive(Line l) { double area=0; double area1=0; double area2=0; double area3=0; double area4=0; double area5=0; double area6=0; if(isOnPeak(l.getPointA())&&isOnPeak(l.getPointB())){ area1=area(l,a,b,c); area2=area(l,a,e,d); area3=area(l,b,c,d); area4=area(l,b,a,e); area5=area(l,c,d,e); area=area1+area2+area3+area4+area5; } else if((isOnPeak(l.getPointA())||isOnPeak(l.getPointB()))){ area=areafour(l); } return area; } //另外一部分的面积 public double areaFive1(Line l) { double area=S()-areaFive(l); return area; } //求四边形小面积 public double areafour(Line l) { double s=0; Point[] point= {a,b,c,d,e}; for(int i=0;i<5;i++) { if((l.getPointA().equals(point[i])||l.getPointB().equals(point[i]))&&i<3) { s=TriangleS(point[i].getX(),point[i].getY(),point[i+1].getX(),point[i+1].getY(),point[i+2].getX(),point[i+2].getY()) +TriangleS(l.getPointA().getX(),l.getPointA().getY(),l.getPointB().getX(),l.getPointB().getY(),point[i+2].getX(),point[i+2].getY()); } else if((l.getPointA().equals(point[i])||l.getPointB().equals(point[i]))&&i>=3) { s=TriangleS(point[i].getX(),point[i].getY(),point[i-1].getX(),point[i-1].getY(),point[i-2].getX(),point[i-2].getY()) +TriangleS(l.getPointA().getX(),l.getPointA().getY(),l.getPointB().getX(),l.getPointB().getY(),point[i-2].getX(),point[i-2].getY()); } } return s; } //求三角形小面积,交两个顶点 public double area(Line l,Point x,Point y,Point z) { double area=0; if((l.getPointA().equals(x)&&l.getPointB().equals(z))||(l.getPointB().equals(x)&&l.getPointA().equals(z))) { area=TriangleS(x.getX(),x.getY(),y.getX(),y.getY(),z.getX(),z.getY()); return area; } else { return area=0; } } } //用于定义一个“点”类 class Point { public double x; public double y; public Point() { } public Point(double x,double y) { this.x=x; this.y=y; } /* 设置坐标x,将输入参数赋值给属性x */ public void setX(double x) { this.x = x; } /* 设置坐标y,将输入参数赋值给属性y */ public void setY(double y) { this.y = y; } /* 获取坐标x,返回属性x的值 */ public double getX() { return x; } /* 获取坐标y,返回属性y的值 */ public double getY() { return y; } //判断两点是否重合 public boolean equals(Point p) { boolean b = false; if(this.x==p.getX()&&this.y==p.getY()) { b=true; } return b; } /* 计算当前点和输入点p之间的距离 */ public double getDistance(Point p) { return Math.sqrt(Math.pow(x-p.getX(), 2)+Math.pow(y-p.getY(), 2)); } } class PointInputError { //判断从字符串中解析出的点的数量是否合格。 public static void wrongNumberOfPoints(ArrayList ps, int num) { if (ps.size() != num) { System.out.println("wrong number of points"); System.exit(0); } } //判断输入的字符串中点的坐标部分格式是否合格。若不符合,报错并退出程序 public static void wrongPointFormat(String s) { if (!s.matches("[+-]?([1-9]\\d*|0)(\\.\\d+)?,[+-]?([1-9]\\d*|0)(\\.\\d+)?")) { System.out.println("Wrong Format"); System.exit(0); } } // 输入字符串是否是"选项:字符串"格式,选项部分是否是1~5其中之一 public static void wrongChoice(String s) { if (!s.matches("[1-5]:.+")) { System.out.println("Wrong Format"); System.exit(0); } }
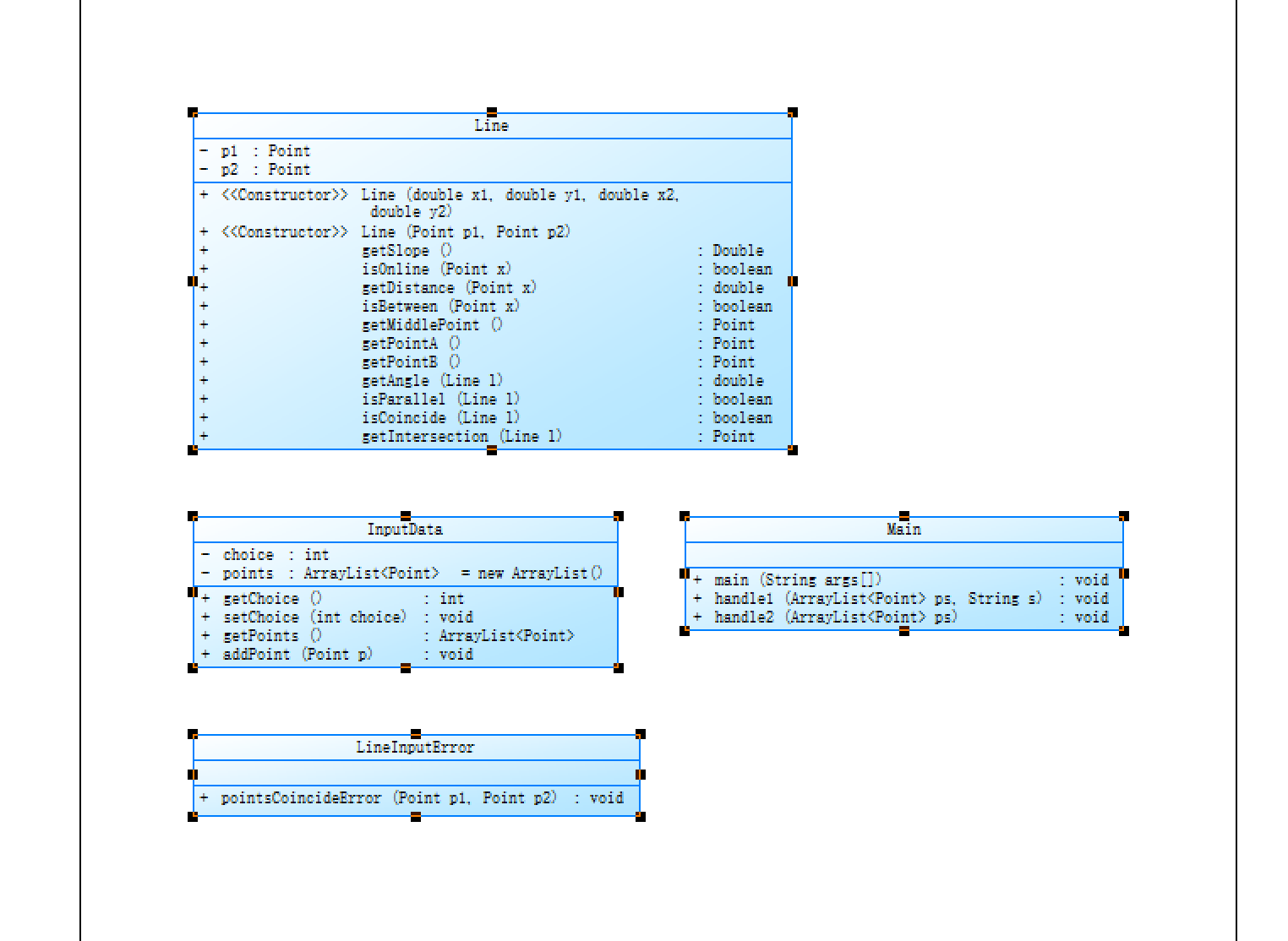
类图如上:还有很多不准确的地方,但会多多改进。
解释与心得:其实第五次pta作业是延续了第四次pta7-2题目的精髓,从三角形到四边形再到五边形,不论是判断多边形的凹凸性,还是判断格式错误,以及点线面之间的关系,Java中许许多多的知识点都在这系列题目中体现,最重要的是类的设计,以及类中的对象的设计,还有各种属性,以及方法的建立以及调用。从最开始的点线面系列,对于我们刚学Java来说,题目写好了,非常能让我们理解与体会类和对象的关系。
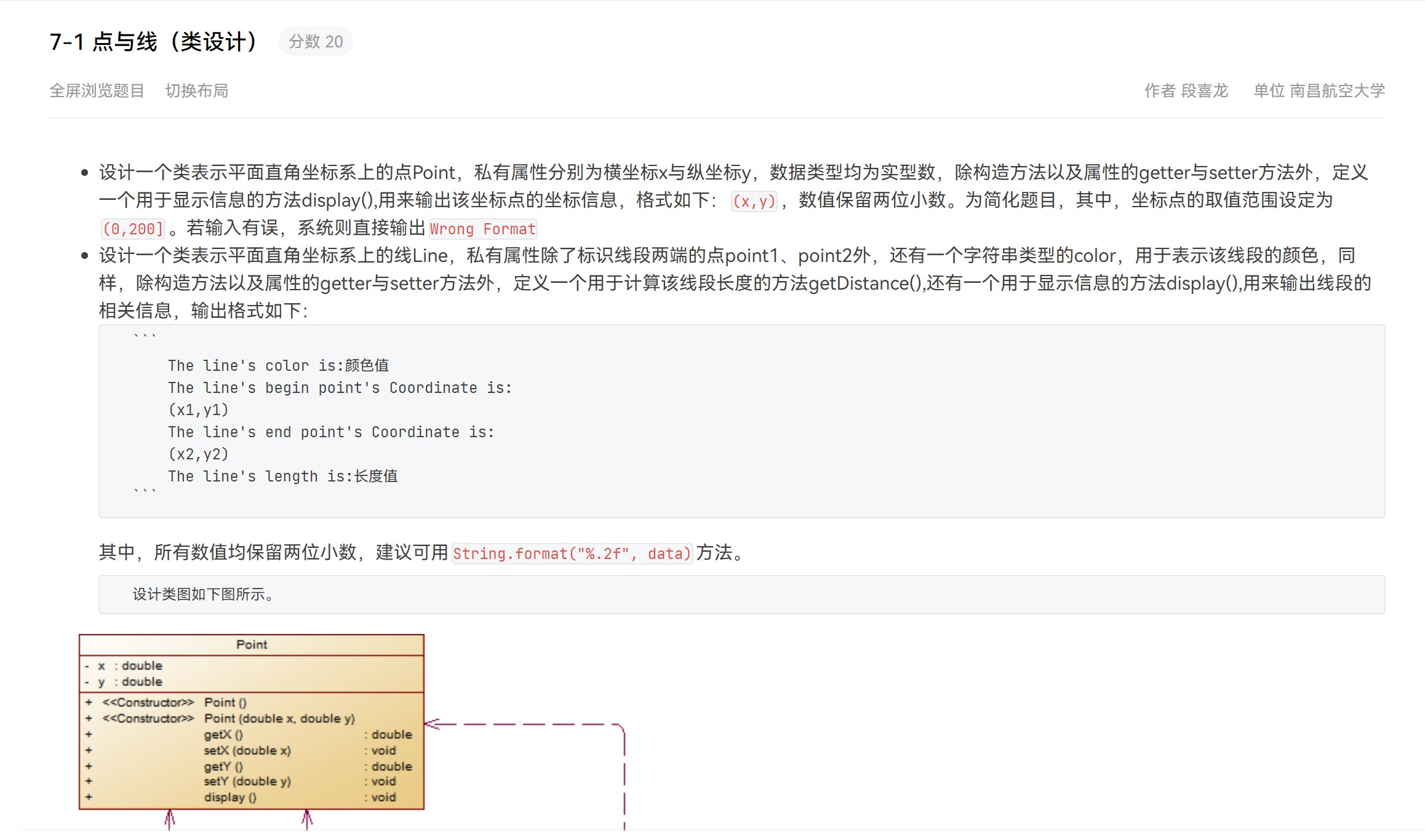
期中考试7-1点与线(类设计)
考试总结:题目为三道,第一道为简单的点和线类的设计,一个point类和line类,基础类的设计和构造方法与属性。第二道为点线面问题重构(继承与多态),第三道为点线面问题再重构(容器类),在“点与线(继承与多态)”题目基础上,对题目的类设计进行重构,增加容器类保存点、线、面对象,并对该容器进行相应增、删、遍历操作。
import java.util.Scanner; import java.lang.Math; class Point{ private double x; private double y; public Point(){ } public Point(double x,double y){ this.x = x; this.y = y; } public double getX() { return x; } public void setX(double x) { this.x = x; } public double getY() { return y; } public void setY(double y) { this.y = y; } public void display(){ System.out.println("("+String.format("%.2f", x)+","+String.format("%.2f", y)+")"); } } class Line { private Point p1; private Point p2; private String color; static Point point = new Point(); public Line(){ } public Line(Point p1,Point p2,String color){ this.p1 = p1; this.p2 = p2; this.color = color; } public Point getP1() { return p1; } public void setP1(Point p1) { this.p1 = p1; } public Point getP2() { return p2; } public void setP2(Point p2) { this.p2 = p2; } public String getColor(){ return color; } public void setColor(String color){ this.color = color; } public double getDistance(){ return Math.sqrt((p1.getY() - p2.getY()) * (p1.getY() - p2.getY()) + (p1.getX() - p2.getX())* (p1.getX() - p2.getX())); } public void display(){ System.out.println("The line's color is:"+color); System.out.println("The line's begin point's Coordinate is:"); p1.display(); System.out.println("The line's end point's Coordinate is:"); p2.display(); System.out.print("The line's length is:"+ String.format("%.2f", getDistance())); } } class Main{ public static void main(String[] args) { Scanner input = new Scanner(System.in); double x1 = input.nextDouble(); double y1 = input.nextDouble(); double x2 = input.nextDouble(); double y2 = input.nextDouble(); if(x1 > 200 || x1 <= 0 || y1 > 200 || y1 <= 0){ System.out.println("Wrong Format"); System.exit(0); } if(x2 > 200 || x2 <= 0 || y2 > 200 || y2 <= 0){ System.out.println("Wrong Format"); System.exit(0); } String color = input.next(); Point point1 = new Point(x1,y1); Point point2 = new Point(x2,y2); Line line = new Line(point1,point2,color); line.display(); } }
解释与心得:
期中考试要求设计点和线,点去组成线,在线中得到点的两个坐标后进行输出。有getColor和getDistance两个方法。并且在主函数里调用自己Display方法进行输出。在做题的时候,我判断输出有碰到问题,当判断超出边界后,应该停止整个程序System.exit(0);在这里浪费了一些时间。另外点传参传x1,y1自己的点,线传参是传点的参,一开始数据传不进去,这里也浪费了不少时间。
7-2点线面问题重构(继承与多态)
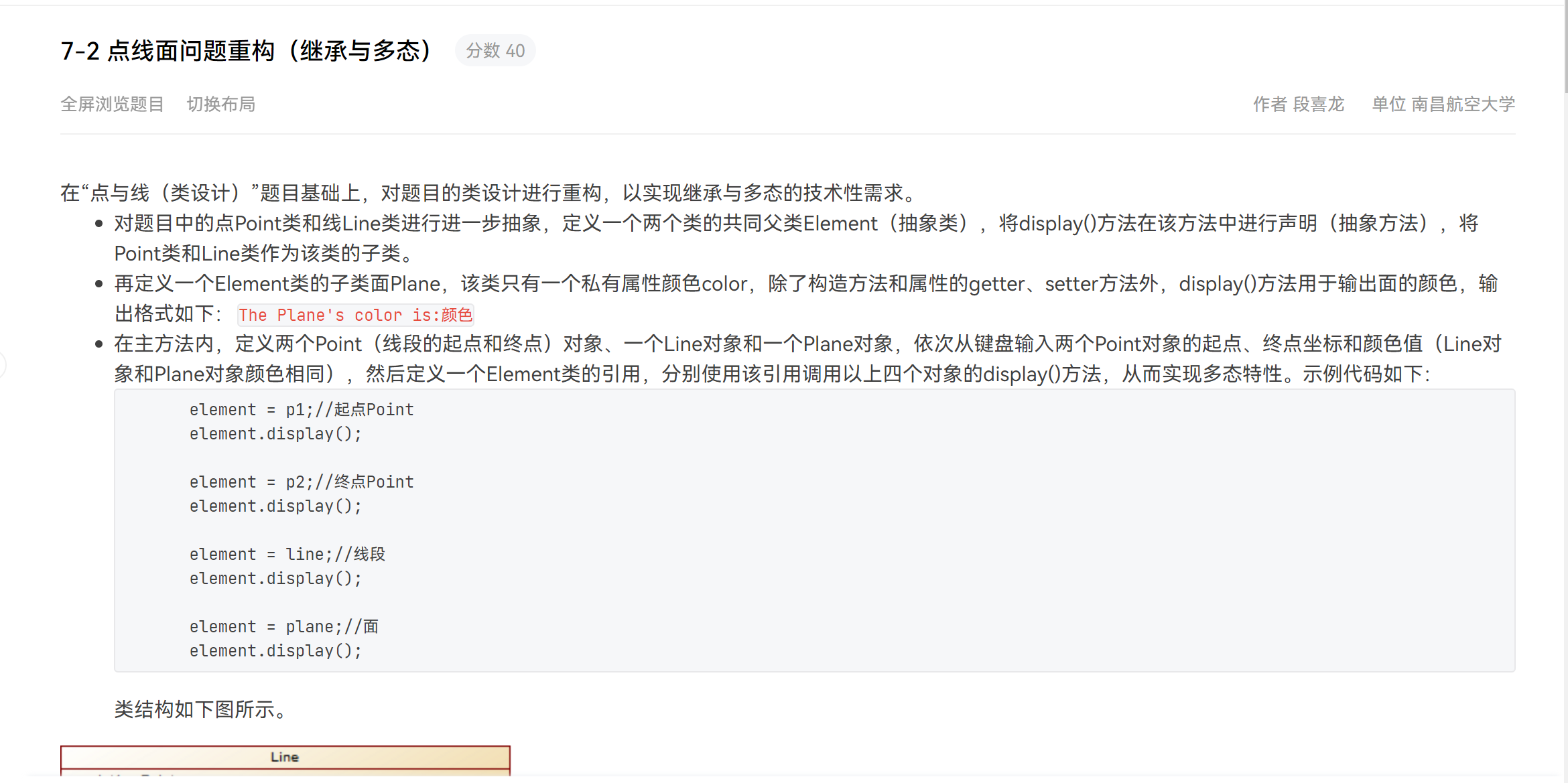
类图如下: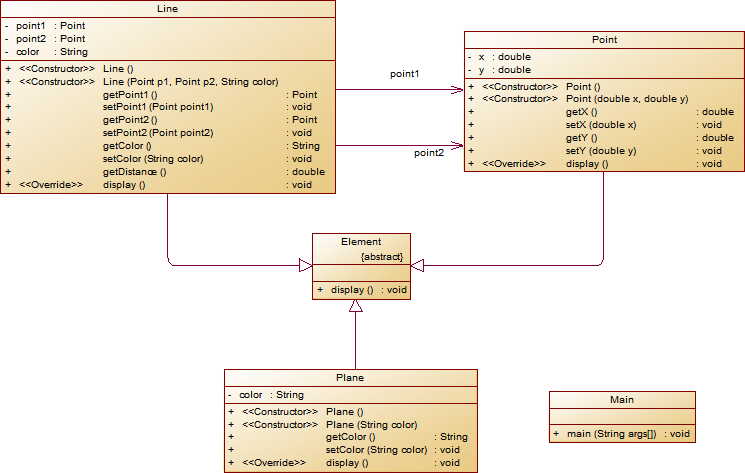
import java.util.Scanner; import java.lang.Math; abstract class Element{ public Element(){ } public abstract void display(); } class Point extends Element{ private double x; private double y; public Point(){ } public Point(double x,double y){ this.x = x; this.y = y; } public double getX() { return x; } public void setX(double x) { this.x = x; } public double getY() { return y; } public void setY(double y) { this.y = y; } @Override public void display(){ System.out.println("("+String.format("%.2f", x)+","+String.format("%.2f", y)+")"); } } class Line extends Element{ private Point p1; private Point p2; private String color; static Point point = new Point(); public Line(){ } public Line(Point p1,Point p2,String color){ this.p1 = p1; this.p2 = p2; this.color = color; } public Point getP1() { return p1; } public void setP1(Point p1) { this.p1 = p1; } public Point getP2() { return p2; } public void setP2(Point p2) { this.p2 = p2; } public String getColor(){ return color; } public void setColor(String color){ this.color = color; } public double getDistance(){ return Math.sqrt((p1.getY() - p2.getY()) * (p1.getY() - p2.getY()) + (p1.getX() - p2.getX())* (p1.getX() - p2.getX())); } @Override public void display(){ System.out.println("The line's color is:"+color); System.out.println("The line's begin point's Coordinate is:"); p1.display(); System.out.println("The line's end point's Coordinate is:"); p2.display(); System.out.println("The line's length is:"+ String.format("%.2f", getDistance())); } } class Main{ public static void main(String[] args) { Scanner input = new Scanner(System.in); double x1 = input.nextDouble(); double y1 = input.nextDouble(); double x2 = input.nextDouble(); double y2 = input.nextDouble(); if(x1 > 200 || x1 <= 0 || y1 > 200 || y1 <= 0){ System.out.println("Wrong Format"); System.exit(0); } if(x2 > 200 || x2 <= 0 || y2 > 200 || y2 <= 0){ System.out.println("Wrong Format"); System.exit(0); } String color = input.next(); Point point1 = new Point(x1,y1); Point point2 = new Point(x2,y2); Line line = new Line(point1,point2,color); point1.display(); point2.display(); line.display(); System.out.print("The Plane's color is:"+line.getColor()); } }
解释与心得:此题为期中考试第二题,此题主考察继承与多态,在第一题的基础上改进,基础也是建立多种类,在类的基础上进行继承与多态,此题输出与第一题相似,也是输出颜色,计算输出距离,输出颜色,以实现继承与多态的技术性需求。
类与类之关系,以及怎样更好的减少类与类之间的关系,在设计代码时,我设计的两个类总是有很多的关联,子类继承父类的功能,这些关系我在解题时依然不清楚。多道练习的训练,是我对类建立的应用,字符串,循环大大熟练,更好的进行数组和字符串,类的运用
还有一题为期中考试第三题,此题建立在第一、二题的基础上。有后余时间将其完成。本题考察点与线间的距离运算问题,本题目与数学结合,难度为输入数字正确进入相应判断运行公式中,正确输出,建立不同的数据类型,调用建立函数,进入计算运行,其他问题为情况不符合情况,判断问题的否定输出等等。本题出现多次Bug,多次看书,在网上查找学习资料,学习,了解,最后进行编程。
三、踩坑心得
下面是我从网上寻找的降低圈复杂度的方法,在今后的学习或者在解决PTA题目时会学着慢慢的渗透和尝试降低圈复杂度的方法。
•Simplifying Conditional Expressions(简化条件表达式)
Decompose Conditional(分解条件式)
Consolidate Conditional Expression(合并条件式)
Consolidate Duplicate Conditional Fragments(合并重复的条件片断)
- 在设计类时,圈复杂度较大,在今后我将学习如何将圈复杂度降低。
- 考试的第一题我没有全面的考虑好,在一方面的考点没有兼顾到导致。
并且经过了那么多的练习之后,我觉得类的设计应该在我们写代码的时候放在第一位,真的很重要。
四、改进建议
1.通过三次的习题集,尤其是题目1(7-4)、题目集3(7-2)这两个题在关于类设计的时候,设计到的程序设计原则,实现同样的功能,类的设计却有好几种可能,怎样使类的设计更加的合理,能大大的提高我们代码的质量。
2.我应多在类方面下功夫,我认为类是可以很好的避免不同的错误。并且学了Java的几个原则之后,更好的体会到了如何完成类的设计。
3.部分框架的使用比c语言数组要简单,运用的更容易,可以帮我们减少很多错误,减少我们在修改时浪费的时间,在今后的设计中,自己要学习使用这些方便的集合框架的,使代码更加的简洁、方便,且实现功能。
4.题目的难度希望是逐渐加深,不是一个题目集中都是很难的题目。
5这三次的习题集,又进一步的提升了我的编程能力,初步形成了面向对象设计的思想,以及类与类之间的关系都得到了一定程度的掌握,这三次习题集的有一定的收获。





