P2495 [SDOI2011]消耗战

P2495 [SDOI2011]消耗战

---

虚树入门题目？？

先链接一波：https://www.cnblogs.com/zzqsblog/p/5560645.html

可以每次做一个树形dp，复杂度\(O(n^2)\)

但是发现每次的dp有很多一样，所以造成很多无用的转移

所以说要尝试搞出所有有用的点来

有用的点也就是给的点+两两之间的lca（在lca需要合并信息了）

这个要算出来并不是平方级别的

直接把给出的点按照dfs序从小到大sort一遍去重即可，证明见下面

然后现在知道了虚树上的点，如何求出虚树？？？

只需要维护一个栈，按dfs序从小到大加点，加点时若栈顶不是该点的祖先就弹栈，然后连接栈顶和这个点就行了。

虚树的边权根据题目而定。比如本题，鸽（注：没错别字）一条边就相当于鸽掉一条链，所以链的权值等于链上边权取min。

然后愉快的dp就星了。

倍增好麻烦。。

记得开longlong.

// It is made by XZZ
#include<cstdio>
#include<algorithm>
#include<set>
#define il inline
#define rg register
#define vd void
#define sta static
typedef long long ll;
using namespace std;
il int gi(){
	rg int x=0,f=1;rg char ch=getchar();
	while(ch<'0'||ch>'9')f=ch=='-'?-1:f,ch=getchar();
	while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
	return x*f;
}
const int maxn=250010;
int fir[maxn],nxt[maxn<<1],dis[maxn<<1],w[maxn<<1],id;
il vd link(int a,int b,int c){nxt[++id]=fir[a],fir[a]=id,dis[id]=b,w[id]=c;}
int dfn[maxn],dep[maxn],f[18][maxn],g[18][maxn];
il vd dfs(int x){
	dfn[x]=++dfn[0];
	for(int i=fir[x];i;i=nxt[i]){
		if(f[0][x]==dis[i])continue;
		dep[dis[i]]=dep[x]+1;
		f[0][dis[i]]=x;
		g[0][dis[i]]=w[i];
		dfs(dis[i]);
	}
}
il int lca(int x,int y){
	if(dep[x]<dep[y])swap(x,y);
	for(rg int i=17;~i;--i)if(dep[f[i][x]]>=dep[y])x=f[i][x];
	for(rg int i=17;~i;--i)if(f[i][x]!=f[i][y])x=f[i][x],y=f[i][y];
	if(x!=y)x=f[0][x];
	return x;
}
il pair<int,int> jump(int x,int k){
	int ret=1e9;
	for(rg int i=17;~i;--i)if(k&(1<<i))ret=min(ret,g[i][x]),x=f[i][x];
	return make_pair(x,ret);
}
int s[maxn<<1],stk[maxn],top;
il int cmp(const int&a,const int&b){return dfn[a]<dfn[b];}
int fir_[maxn],nxt_[maxn],dis_[maxn],w_[maxn],id_;
ll F[maxn];
il vd link_(int a,int b,int c){nxt_[++id_]=fir_[a],fir_[a]=id_,dis_[id_]=b,w_[id_]=c;}
int fafa[maxn];
il vd dp(int x,ll lst=1e18){
	F[x]=lst;ll sum=0;
	if(fafa[s[x]]==fafa[0])return;
	for(int i=fir_[x];i;i=nxt_[i]){
		int y=dis_[i],z=w_[i];
		dp(y,z);
		sum+=F[y];
	}
	if(sum<F[x])F[x]=sum;
}
main(){
#ifdef xzz
	freopen("2495.in","r",stdin);
	freopen("2495.out","w",stdout);
#endif
	int n=gi(),a,b,c;
	for(rg int i=1;i<n;++i)a=gi(),b=gi(),c=gi(),link(a,b,c),link(b,a,c);
	dep[1]=1;dfs(1);
	for(rg int i=1;i<18;++i)
		for(rg int j=1;j<=n;++j){
			f[i][j]=f[i-1][f[i-1][j]];
			g[i][j]=min(g[i-1][j],g[i-1][f[i-1][j]]);
		}
	int m,q=gi();
	for(rg int yyb=1;yyb<=q;++yyb){
		m=gi();
		for(rg int i=1;i<=m;++i)s[i]=gi(),fafa[s[i]]=yyb;
		fafa[0]=yyb;
		sort(s+1,s+m+1,cmp);
		for(rg int i=1;i<m;++i)s[i+m]=lca(s[i],s[i+1]);
		s[m+m]=1;
		m+=m;
		sort(s+1,s+m+1,cmp);
		m=unique(s+1,s+m+1)-s-1;
		top=0;
		id_=0;
		for(rg int i=1;i<=m;++i)fir_[i]=0;
		for(rg int i=1;i<=m;++i){
			while(top&&(dep[s[stk[top]]]>=dep[s[i]]||jump(s[i],dep[s[i]]-dep[s[stk[top]]]).first!=s[stk[top]]))--top;
			if(top)link_(stk[top],i,jump(s[i],dep[s[i]]-dep[s[stk[top]]]).second);
			stk[++top]=i;
		}
		dp(1);
		printf("%lld\n",F[1]);
	}
	return 0;
}

---

证明：

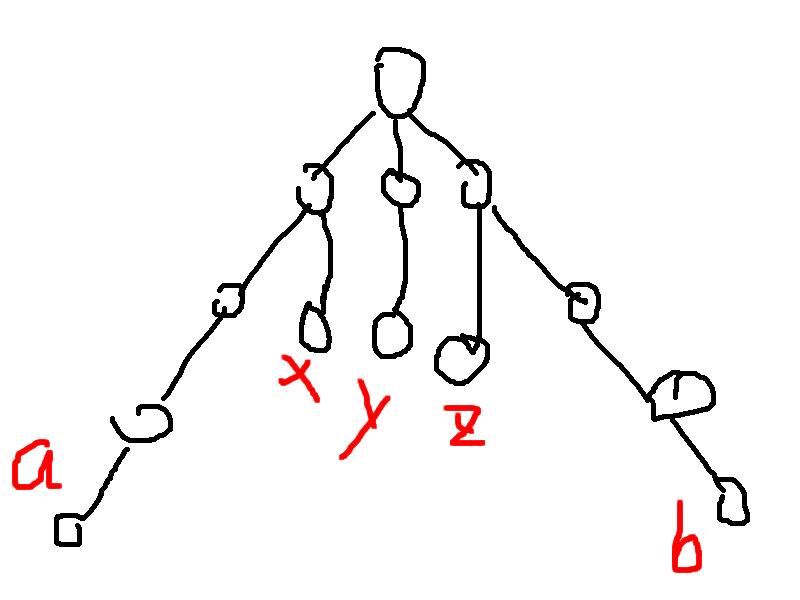
假设现在有两个点a，b的dfs序不相邻，那么中间一定有一个点c。我们证明lca(a,b)一定在虚树中。

c的可能位置是x,y,z。

若c在x的话，lca(a,x)在虚树中，我们只需要证lca(x,b)在虚树中就星了。

c在y的话直接得证。

c在z同c在x。lca(z,b)在虚树中，我们只需要证lca(a,z)在虚树中就星了。

那么如此递归证下去总会到c在y位置的情况或者a，b的dfs序相邻的情况。

所以证完了。