广义后缀自动机学习笔记
广义后缀自动机
Tags:字符串 题解
作业部落
评论地址
一、前言
广义后缀自动机实际上考得比普通后缀自动机要更多更灵活
所以这里作为一个小专题呈现,题单在后缀自动机的总题单里
为了更好掌握广义\(SAM\),这里提供一个高级模板题的题解
二、构建方法
普通后缀自动机处理单串的问题,多串就只能使用广义\(SAM\)了
最方便的构建
一种方案是把字符串中间依次用从未出现过的字符连接,当作一个字符串处理,再多几个特判
for(int i=1;i<=m;i++)
{
string A; cin>>A; s[++l]='#';
for(int j=0,l=A.size();j<l;j++) s[++l]=A[j];
}
一种方案是每插入一个串就把\(lst=1\),其余什么都不用改变
for(int i=1;i<=m;i++)
{
lst=1; cin>>s; l=s.size();
for(int j=0;j<l;j++) Extend(s[j]-'0');
}
最准确的构建
其实准确来说,广义后缀自动机是通过遍历Trie树建的,所以要先建好\(Trie\)树
每次找到\(fa[x]\)的节点作为\(lst\)往后接即可
有两种方法:\(BFS\)与\(DFS\)遍历建后缀自动机
叶大佬告诉我们,\(DFS\)会被卡成\(n^2\)而\(BFS\)不会,就像下面图片中的例子
int Extend(int f,int c)
{
if(ch[f][c]&&len[ch[f][c]]==len[f]+1) return ch[f][c];//?!
int p=++node,ff=0;lst=p;
len[p]=len[f]+1;
while(f&&!ch[f][c]) ch[f][c]=p,f=fa[f];
if(!f) {fa[p]=1;return p;}
int x=ch[f][c],y=++node;
if(len[x]==len[f]+1) {fa[p]=x;node--;return p;}
if(len[p]==len[f]+1) ff=1;//?!
memcpy(ch[y],ch[x],sizeof(ch[y]));
len[y]=len[f]+1; fa[y]=fa[x]; fa[x]=fa[p]=y;
while(f&&ch[f][c]==x) ch[f][c]=y,f=fa[f];//原因就在这
return ff?y:p;
}
你会发现这和后缀自动机的模板有些区别诶
首先是有一个返回值,这个很好理解,返回的是如果下次要往后接的\(lst\),也就是方便找到\(Trie\)树某点在\(SAM\)上的位置,直接传进来就好啦
然后是有一个if(len[p]==len[f]+1) return y;的特判
前面也有一个if(ch[f][c]&&len[ch[f][c]]==len[f]+1) return ch[f][c];的特判
好,广义\(SAM\)的构建就讲完了
什么?!WTF?!那个特判是啥意思我还不造嘞!
别急,我们来通过例题理解它
三、例题
链接:HN省队集训
题意:给\(n\)个字符串\(s\),强制在线进行\(4\)个操作,询问/串长\(1e5\),\(n\le20\)

题解
对于操作\(1\)
记录\(pos[i][j]\)表示在第\(i\)次操作后\(j\)号串的结尾字符在\(SAM\)上的节点编号是\(j\),当在第\(i\)次操作在字符串\(x\)后插入字符时,令\(lst=pos[i-1][x]\),然后照常插入即可
对于操作\(2\)
记录\(siz[i][j]\)表示在\(i\)号点,贡献给\(j\)号字符串的\(Endpos\)集合的大小,实际意义就是\(i\)号点代表的字符串集合在\(n\)个串中共出现了\(\sum_{j=1}^{n}siz[i][j]\),其中在\(j\)号串中出现了\(siz[i][j]\)次。
查询\(z\)串中\(x\)串的出现次数,那么\(x\)串在\(y\)次操作后的结尾位置是\(pos[y][x]\),那么\(siz[pos[y][x]][z]\)就是答案。
这里的\(siz\)是在\(parent\)树上对子树进行求和才有上述意义,原理可见于我的另一篇博文后缀自动机,但是这里需要在线插入节点,于是我们用\(lct\)维护\(parent\)树上的\(siz\),每次断开或者连上父亲的时候相当是给节点到\(parent\)根的路径\(+/-1\),所以这里的\(lct\)只需要支持链加,不需要改变树的根所以没有\(makeroot\)、\(reverse\)等操作,如果需要学习\(lct\),可见我的另一篇博文lct
对于操作\(3\)
维护一个全局变量\(sum\),每个节点贡献的本质不同的子串个数就是\(len[x]-len[fa[x]]\)
对于操作\(4\)
在\(SAM\)上匹配到T的结束位置的节点,\(Ans=max(siz[pos][i]),i=1..n\)
复杂度分析
操作\(1\)的总复杂度是\(\sum len[s_i]×log(n)×20\)的,操作\(2\)是\(log(n)\)的,操作\(3\)是\(O(1)\),操作\(4\)是\(\sum len[T_i]+20\)的,\(log\)都是\(lct\)的复杂度
所以总共时间复杂度是\(O(\sum len[s_i]*log(n)+\sum len[T_i])\)的
空间复杂度\(O(\sum|S|*logn*20)\)左右
代码如下
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#define ll long long
using namespace std;
int read()
{
char ch=getchar();int h=0,t=1;
while((ch>'9'||ch<'0')&&ch!='-') ch=getchar();
if(ch=='-') t=-1,ch=getchar();
while(ch>='0'&&ch<='9') h=h*10+ch-'0',ch=getchar();
return h*t;
}
const int N=1e6+100;
char s[N];
int n,zx,m,ans,node=1;
int fa[N],ch[N][11],len[N],pos[N][21];
ll sum;
namespace lct
{
#define lc t[x].ch[0]
#define rc t[x].ch[1]
struct LCT{int fa,ch[2],val[21],tag[21];}t[N];
int isrt(int x) {return t[t[x].fa].ch[0]!=x&&t[t[x].fa].ch[1]!=x;}
void Tag(int x,int y,int k) {t[x].val[y]+=k; t[x].tag[y]+=k;}
void pushdown(int x)
{
for(int i=1;i<=n;i++)
{
if(!t[x].tag[i]) continue;
if(lc) Tag(lc,i,t[x].tag[i]);
if(rc) Tag(rc,i,t[x].tag[i]);
t[x].tag[i]=0;
}
}
void rotate(int x)
{
int y=t[x].fa,z=t[y].fa;
int k=t[y].ch[1]==x;
if(!isrt(y)) t[z].ch[t[z].ch[1]==y]=x; t[x].fa=z;
t[y].ch[k]=t[x].ch[k^1]; t[t[x].ch[k^1]].fa=y;
t[x].ch[k^1]=y; t[y].fa=x;
}
void Push(int x){if(!isrt(x)) Push(t[x].fa);pushdown(x);}
void splay(int x)
{
Push(x);
while(!isrt(x))
{
int y=t[x].fa,z=t[y].fa;
if(!isrt(y)) (t[z].ch[0]==y)^(t[y].ch[0]==x)?rotate(x):rotate(y);
rotate(x);
}
}
void Access(int x) {for(int y=0;x;y=x,x=t[x].fa) splay(x),rc=y;}
void Add(int x,int y,int op) {for(int i=1;i<=n;i++) Tag(x,i,t[y].val[i]*op);}
void link(int x,int y) {Push(x);t[x].fa=y;Access(y);splay(y);Add(y,x,1);}
void cut(int x) {Access(x);splay(x);Add(lc,x,-1);lc=t[lc].fa=0;}
int query(int x,int k) {Push(x);return t[x].val[k];}
}
int Extend(int f,int id,int c)
{
if(ch[f][c]&&len[ch[f][c]]==len[f]+1)
{
int p=ch[f][c];
lct::Access(p);lct::splay(p);lct::Tag(p,id,1);
return p;
}
int p=++node; len[p]=len[f]+1; lct::t[p].val[id]=1;
while(f&&!ch[f][c]) ch[f][c]=p,f=fa[f];
if(!f) {fa[p]=1;lct::link(p,1);sum+=len[p]-len[fa[p]];return p;}
int x=ch[f][c];
if(len[f]+1==len[x]) {fa[p]=x;lct::link(p,x);sum+=len[p]-len[fa[p]];return p;}
if(len[f]+1==len[p])//!!
{
lct::cut(x);lct::link(p,fa[x]);lct::link(x,p);
memcpy(ch[p],ch[x],sizeof(ch[p]));
fa[p]=fa[x]; fa[x]=p;
sum-=len[p]-len[fa[p]];
while(f&&ch[f][c]==x) ch[f][c]=p,f=fa[f];
}
else
{
int y=++node; len[y]=len[f]+1;
lct::cut(x);lct::link(y,fa[x]);lct::link(x,y);lct::link(p,y);
memcpy(ch[y],ch[x],sizeof(ch[y]));
fa[y]=fa[x]; fa[x]=fa[p]=y;
while(f&&ch[f][c]==x) ch[f][c]=y,f=fa[f];
}
sum+=len[p]-len[fa[p]];
return p;
}
int calc()
{
int x=1,res=0,i,l; scanf("%s",s+1);
for(i=1,l=strlen(s+1);i<=l&&x;i++) x=ch[x][s[i]-'0'];
if(i!=l+1) return 0;
lct::Push(x);
for(i=1;i<=n;i++) res=max(res,lct::t[x].val[i]);
return res;
}
int main()
{
n=read();zx=read();
for(int i=1;i<=n;i++)
{
scanf("%s",s+1); pos[0][i]=1;
for(int p=1,l=strlen(s+1);p<=l;p++)
pos[0][i]=Extend(pos[0][i],i,s[p]-'0');
}
m=read();
for(int i=1;i<=m;i++)
{
int op=read(),x,y,z;
for(int p=1;p<=n;p++) pos[i][p]=pos[i-1][p];
if(op<=2) x=read(),y=read();
if(op==1) y=(y^(ans*zx))%10,pos[i][x]=Extend(pos[i][x],x,y);
else if(op==2) z=read(),printf("%d\n",ans=lct::query(pos[y][x],z));
else if(op==3) printf("%lld\n",sum);
else printf("%d\n",ans=calc());
}
return 0;
}
Wait!
出题人和我讲这道题的时候,特别强调要特判!
但是我一直不理解,把特判if(len[f]+1==len[p]) ff=1;删了后还是过了本题
于是他给了一组\(hackdata\)并且在\(BZOJ\)加强了数据
Input
2 0
3201
01
1
2 2 0 1
Output
Right : 1
Wrong : 0
首先我们建出第一个串的\(SAM\)(黑边是\(SAM\)上的边,基佬紫边是\(Parent\)树上的边)
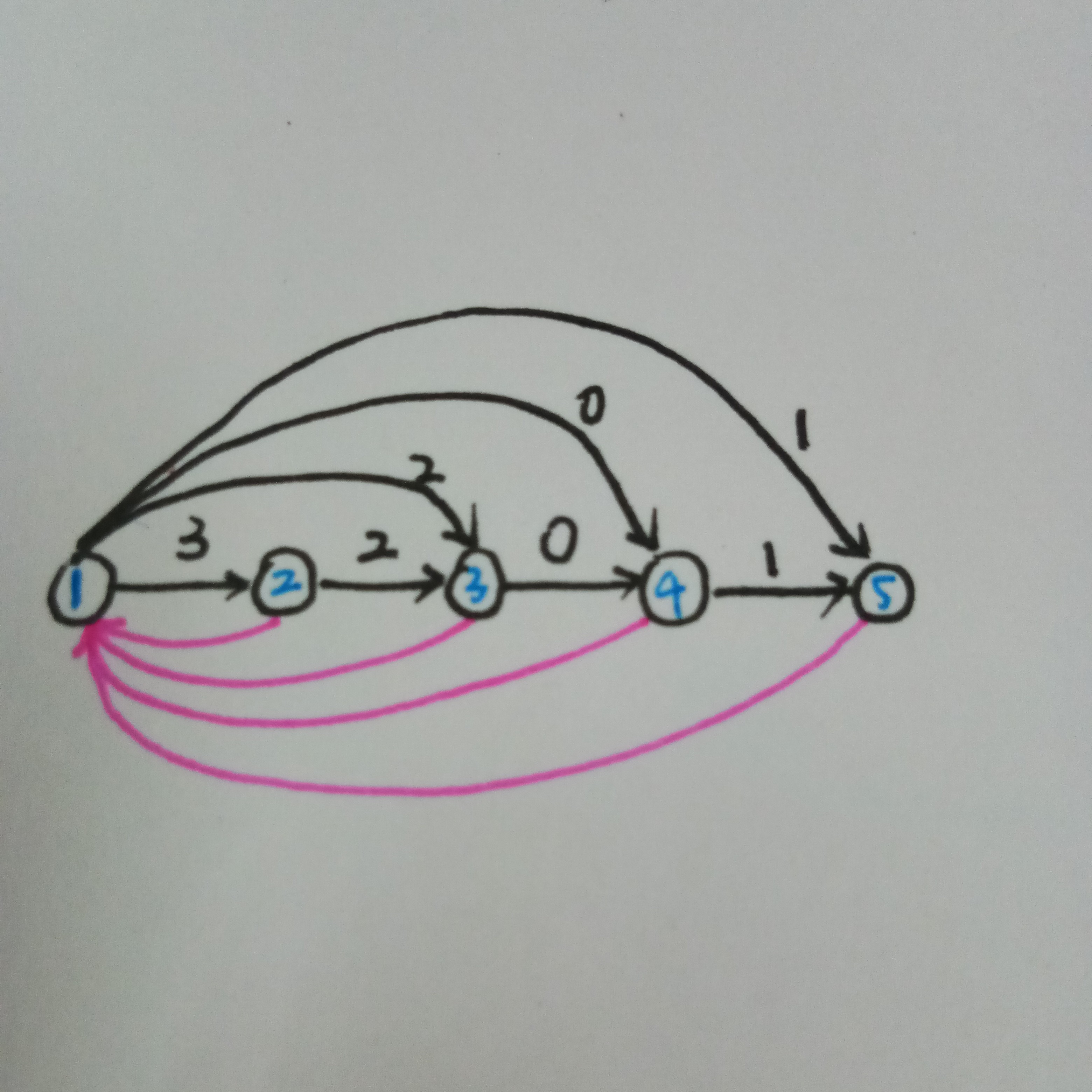
我们先加特判,那么继续建就会这样(姨妈红边是删去的边)
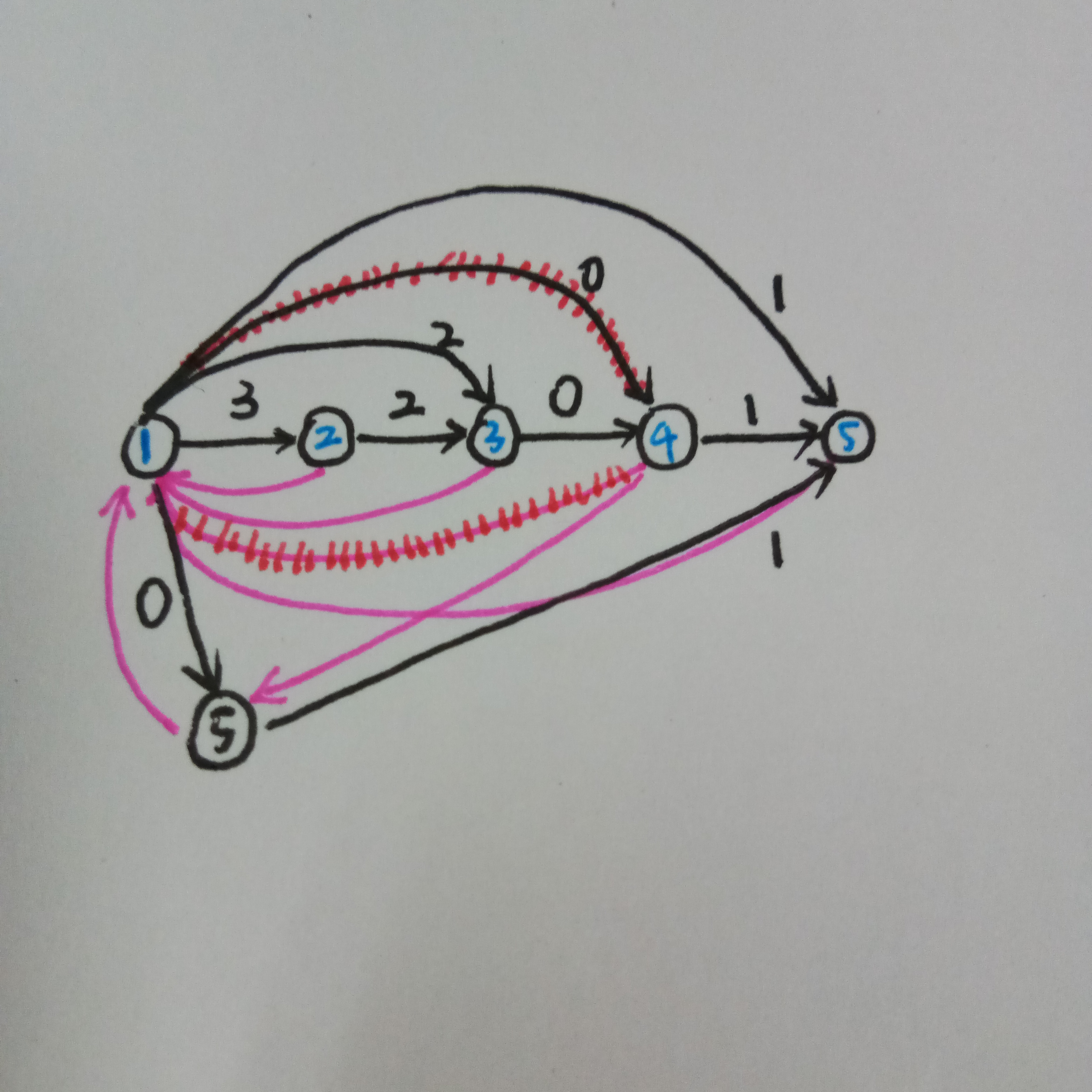
继续加边
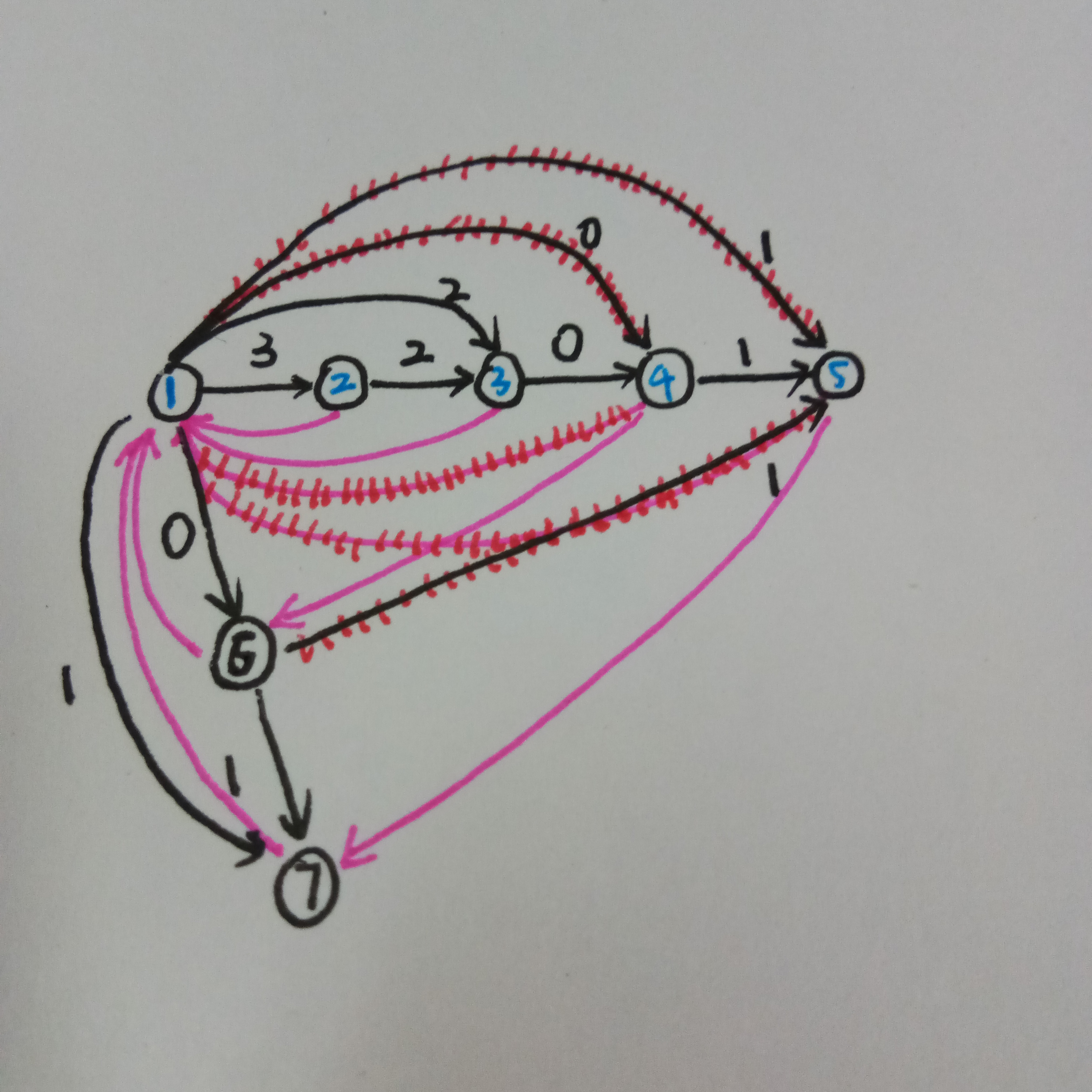
但是如果不加这个特判,就会撒夫夫地把蓝\(4\)给复制一边,但是这时第二个串的\(0\)的结尾位置是\(5\),当我查询\(2\)串在\(1\)串中出现次数就会访问到\(siz[pos[x][2]][1]\),此时很遗憾地发现调用到了\(5\)节点,它没有记录蓝\(4\)的信息
这样写代码很长,有没有一种简单的写法捏?
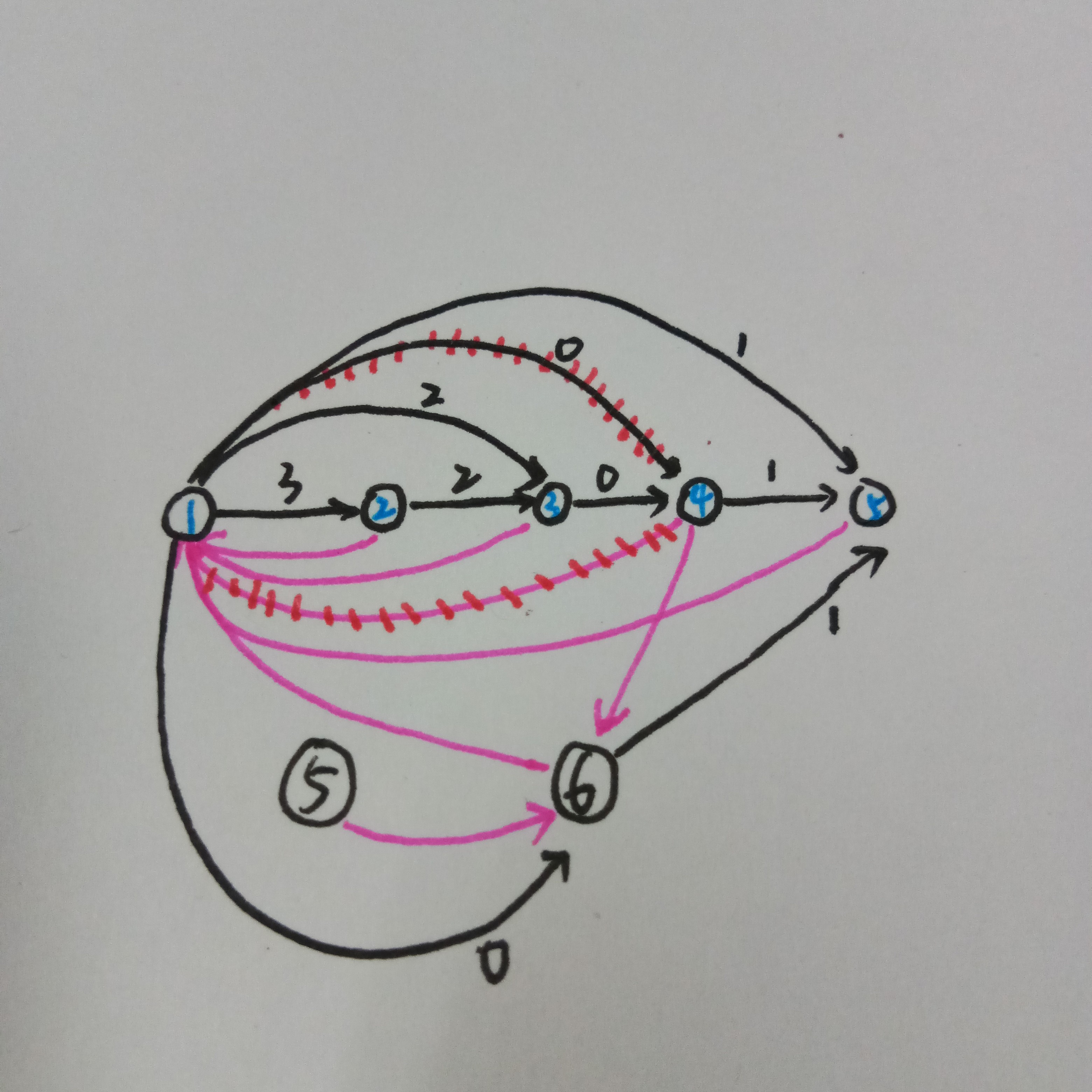
有的,我们发现黑\(5\)不会再被访问到,相当于他的贡献被算到了六号点上,同时又没有点指向它所以它不会被访问到。对比上面两张图,我们发现其实就是\(图1\)中的黑\(5\)和\(图3\)中的黑\(6\)是完全一样的诶!
于是直接返回黑\(6\)就好啦
把上述代码的\(Extend\)改成下面这种
int Extend(int f,int id,int c)
{
if(ch[f][c]&&len[ch[f][c]]==len[f]+1)
{
int p=ch[f][c];
lct::Access(p);lct::splay(p);lct::Tag(p,id,1);
return p;
}
int p=++node,ff=0; len[p]=len[f]+1; lct::t[p].val[id]=1;
while(f&&!ch[f][c]) ch[f][c]=p,f=fa[f];
if(!f) {fa[p]=1;lct::link(p,1);sum+=len[p]-len[fa[p]];return p;}
int x=ch[f][c];
if(len[f]+1==len[x]) {fa[p]=x;lct::link(p,x);sum+=len[p]-len[fa[p]];return p;}
if(len[f]+1==len[p]) ff=1;
int y=++node; len[y]=len[f]+1;
lct::cut(x);lct::link(y,fa[x]);lct::link(x,y);lct::link(p,y);
memcpy(ch[y],ch[x],sizeof(ch[y]));
fa[y]=fa[x]; fa[x]=fa[p]=y;
while(f&&ch[f][c]==x) ch[f][c]=y,f=fa[f];
sum+=len[p]-len[fa[p]];
return ff?y:p;
}
是不是很方便?
从本质上分析这两个特判
if(ch[f][c]&&len[ch[f][c]]==len[f]+1) return ch[f][c];
我们建\(SAM\)是在\(Trie\)树上遍历建的,这句话表示访问到\(Trie\)树上一个点,它在\(SAM\)上已经被建出来了,所以不需要新建
if(len[f]+1==len[p]) ff=1;
这句特判起作用的条件是中间\(f\)没有被改变,也就是说存在\(ch[f][c]\),假设\(f\)表示的字符串是\(A\),那么插入字符\(c\)后产生\(Ac\),但是\(Ac\)已经存在于自动机上,所以要把它从原来的状态剥离出来,复制一遍,从后来的操作中可以发现最后我们需要的\(lst\)也就是\(return\)的点应该是复制出来的那个点

