后缀自动机学习笔记

后缀自动机(SAM)

抱歉，图床挂了，博主并没有存图，待修改，暂留坑

Tags：字符串

作业部落

评论地址

---

一、SAM详解

博主第一次这么详细地讲解算法,强烈建议看看hihocoder上的讲解
注意弄清楚每个数组的确切含义

1、干嘛用

构建一个自动机，使得一个字符串的所有子串都能够被表示出来
而且从根出发的任意一条合法路径都是该串中的一个子串
后缀自动机是一个DAG（$AC$自动机建成了$Trie$图）

2、复杂度

时间空间都是$O(n)$（空间要开两倍）

3、$len$

$len[i]$表示$i$点表示的字符串集合中最长字符串的长度

从$hihocoder$上可以知道，一个节点表示的$Endpos$（位置集合）对应的字符串的集合中的字符串一定是长度连续的，即有一个$longest$和一个$shortest$
这里的$len$表示的是$longest$，当$shortest$减去其第一个字符，一定会成为另一个节点的$longest$，那么$i$节点的$shortest$便是某节点的$longest+1$

4、$Parent$树

$fa[i]$表示$i$在$Parent$树上的父亲

那么上文所说的$i$所对应另一个节点$j$，使得$shortest(i)=longest(j)+1$，在$parent$树上的关系就是$fa[i]=j$
可以得出，$parent$树一定是树的结构，而且根是$1$号节点，表示的是空串

5、添加一个字符

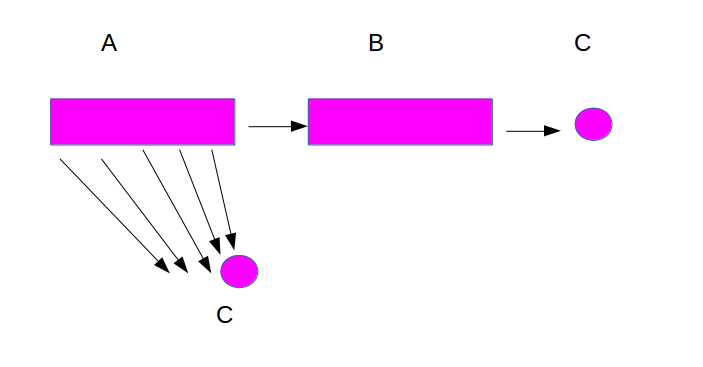
图中很多边都没有画出来
加入一个字符$c$时，把图分为$A,B$两部分，$A$表示这一段存在儿子$C$，$B$表示不存在儿子$C$
我们把右边那个$C$叫作$p$点，把下面的叫$x$好啦

Situation 1

不存在$A$部分，那么沿着$parent$树一直会跳到$0$节点
这个时候其实是没有出现过字符$c$，我们需要把$B$中所有节点的$c$儿子置为$p$号点
其实就是添加了所有以$c$结尾的子串的路径
所以$p$节点代表的$Endpos$对应的字符串的$shortest$为$1$，$parent$树上父亲指向根节点即$1$节点

Situation 2

令$A$中最末端节点编号为$f$，当$longest(f)+1=shortest(x)=longest(x)$时，$x$表示的$Endpos$对应的字符串集只有一个元素

考虑是什么实际情况使得$x$的字符集中只有一个元素：
由于自动机是一个DAG，所以此情况当且仅当从根出发只有一条路径能够到达$x$点，所以从$1$出发到达在$x$点之前的点也只有一条路径，而这条路径如果有不相同的字符，那么不行（比如$aab$，我们需要在自动机上表示子串$b$，所以一定有一条直接往$b$走的路径，而$aaa$就可以说最后一个$a$只有一条路径能够到达，因为加入第三个$a$产生三个子串$a,aa,aaa$，前两个已经能够被表示出来了）所以只有开头一段连续相同的字符满足这种情况

把$p$的$parent$树上父亲指向$x$
其实这个是和第三种情况一样的，因为这里x的入度只为1，如果把这个点复制了一边那么原来的点就没用了

本来以为为了节省空间就这样做，然后发现这样会$WA$，和$SYC$讨论了两天最终得出结果：
1.这个点被复制，那么复制出来的点其实是表示空串，在Parent树上和后缀自动机上都没有意义
2.本以为这样是对的：从原来的点的$Parent$父亲连向复制的点，这样可以贡献$1$的$siz$，使得点被完全复制，原来的点被完全抛弃，但是调试一天发现原来被丢弃的点是有可能被跳$Parent$树访问到的（如图），然后它的$fa$和各项数据会被魔改，使得$siz$贡献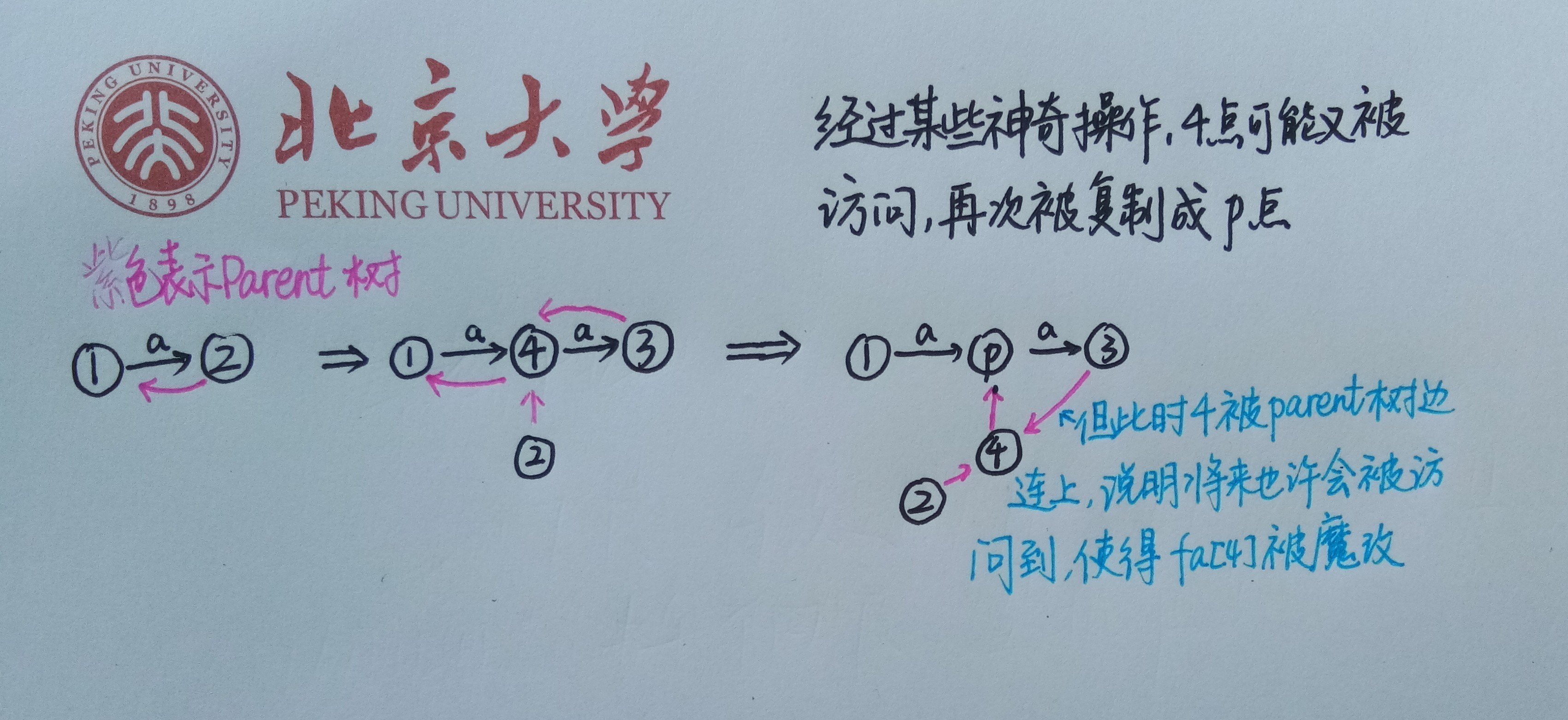不上去

所以第二种情况就是第二种，和第三种有本质区别

Situation 3

把$x$节点复制一遍给$y$，所有前面连续的一段本应该连向$x$的都连向$y$（也就是说在$A$前面可能还有连向$x$的边），把$x$的儿子memcpy给$y$，把$x$和$p$的$parent$父亲连向$y$，把$y$的$len$设置为$len[f]+1$
（Update2018.8.28：已更正@SSerxhs）

比如$aabab$在加入第二个$b$时子串$ab$已经存在，所以$ab$的$Endpos$集合变大了，这样原来第一个$b$表示$aab,ab,b$，它们的$Endpos$都是$3$，而现在只能表示$aab$的$Endpos$是$3$，$ab,b$的$Endpos$是$3,5$，所以需要一个新的点来维护，同时这样操作也保证了如果在后面加入$c$，只会增加$c,bc,abc$而不会增加$aabc$

$len[y]=len[f]+1$：在后面接一个字符，所以$longest$直接加$1$
一个想了很久的问题：为什么只连前面第一段？
感性理解一下，其实前面一定只有连续的一段连向这个点，所以其实加这句是保证复杂度的

6、siz/sum

$siz[i]$表示$i$号点代表的$Endpos$集合大小，也可以说是$i$号点字符串集合在整个串中的出现次数

• 从parent树上累加

siz[i]=k 表示i节点对应的Endpos的字符串集合出现了k次

for(int i=node;i>=1;i--) siz[fa[A[i]]]+=siz[A[i]];
//A[i]表示len数组第从大到小第i位的节点

因为parent树上父亲的所有字符串是所有儿子的所有字符串的后缀，所以所有儿子出现的地方父亲一定会出现，那么siz[i]+=siz[son[i]]

$sum[i]$表示后缀自动机上经过$i$点的子串数量

• 从自动机上累加

sum[i]=k 表示字符串中经过i号节点的本质不同的子串有多少个

for(int i=2;i<=node;i++) sum[i]=siz[i]=1;
for(int i=node;i>=1;i--)
    for(int k=0;k<26;k++)
        if(ch[A[i]][k]) sum[A[i]]+=sum[ch[A[i]][k]];

这样相当于在每一个本质不同的子串的结尾打上1的标记，然后sum[i]表示的就是DAG上拓扑序在i之后的点的数量

建议完成这题：[TJOI2015]弦论
这是我的题解

7、构建代码

int fa[N],ch[N][26],len[N],siz[N];
int lst=1,node=1,l;//1为根，表示空串
void Extend(int c)
{
	/*
	  2+2+2+3行，那么多while但是复杂度是O(n)
	 */
	int f=lst,p=++node;lst=p;
	len[p]=len[f]+1;siz[p]=1;
	/*
	  f为以c结尾的前缀的倒数第二个节点，p为倒数第一个（新建）
	  len[i] 表示i节点的longest，不用记录shortest（概念在hihocoder后缀自动机1上讲得十分详细）
	  siz[i]表示i节点所代表的endpos的集合元素大小，即所对应的字符串集的longest出现的次数
	  不用担心复制后点的siz，在parent树上复制后的点的siz是它所有儿子siz之和，比1多
	 */
	while(f&&!ch[f][c]) ch[f][c]=p,f=fa[f];
	if(!f) {fa[p]=1;return;}
	/*
	  把前面的一段没有c儿子的节点的c儿子指向p
	  Situation 1 如果跳到最前面的根的时候，那么把p的parent树上的父亲置为1
	 */
	int x=ch[f][c],y=++node;
	if(len[f]+1==len[x]) {fa[p]=x;node--;return;}
	/*
	  x表示从p一直跳parent树得到的第一个有c儿子的节点的c儿子
	  Situation 2 如果节点x表示的endpos所对应的字符串集合只有一个字符串，那么把p的parent树父亲设置为x
	 */
	len[y]=len[f]+1; fa[y]=fa[x]; fa[x]=fa[p]=y;
	memcpy(ch[y],ch[x],sizeof(ch[y]));
	while(f&&ch[f][c]==x) ch[f][c]=y,f=fa[f];
	/*
	  Situation 3 否则把x点复制一遍（parent树父亲、儿子），同时len要更新
	             （注意len[x]!=len[f]+1,因为通过加点会使x父亲改变）
				  然后把x点和p点的父亲指向复制点y，再将前面所有本连x的点连向y
	 */
}

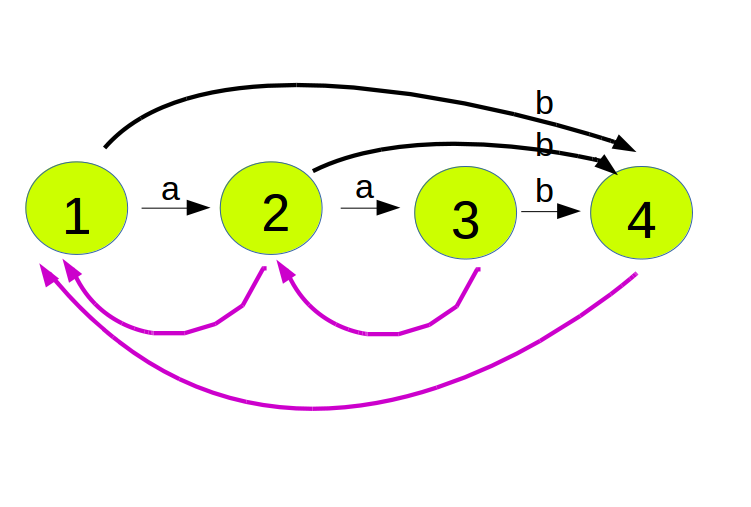
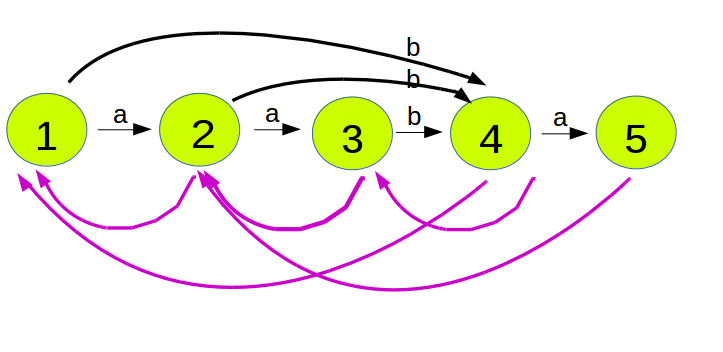
8、构建图示

$aab$

$aaba$

$aabab$

9、性质及应用

桶排序

按照$len$桶排序之后也就是$Parent$树的$BFS$序/自动机的拓扑序
所以按照类似$SA$的桶排序方法可以如下将$Parent$树从叶子到根/自动机反拓扑序用$A[1]..A[node]$表示出来

for(int i=1;i<=node;i++) t[len[i]]++;
for(int i=1;i<=node;i++) t[i]+=t[i-1];
for(int i=1;i<=node;i++) A[t[len[i]]--]=i;

SAM上每一条合法路径都是字符串的一个子串

通过拓扑序DP可以用来求本质不同的子串的问题

SAM上跑匹配

$T$表示查询串，$p$表示匹配到自动机上$p$号节点，$tt$表示当前匹配长度为$tt$
一共分三步
$Step 1$ 一直跳$parent$父亲，直到根或者下一位可以匹配为止，这一步很像$kmp$的$next$和$AC$自动机的$fail$
$Step 2$ 如果匹配得上更新$p$和$tt$，否则重置$p$和$tt$
$Step 3$ 匹配完成则累加答案

for(int i=1;i<=l;i++)
{
	int c=T[i]-'a';
	while(p!=1&&!ch[p][c]) p=fa[p],tt=len[p];
	ch[p][c]?(p=ch[p][c],tt++):(p=1,tt=0);
	if(tt==l) Ans+=siz[p];
}

大多数题肯定没有那么裸，这时需要魔改中间步骤，使得符合题意（Example）

广义后缀自动机

专题太大请见链接
附模板题[HN省队集训6.25T3]string题解

简单地总结

需要知道的几个性质：
1.$SAM$上每条合法路径都是原串中的一种子串
2.一个点可以表示一个字符串集合
3.从一个点跳$Parent$树父亲一直到根，这些字符串集合表示的是所有后缀

新增一个节点$p$，相当于在所有后缀后再加上一个字符
理所当然要一直跳$Parent$树添$c$儿子
1.直接跳到了根，把新增点的$Parent$树父亲置为$1$，$return$
2.如果到某步有个点有$c$儿子，而且该点只能表示一个字符串，那么$fa[p]=ch[f][c]$因为满足了性质$3$，你接着从$p$出发跳父亲得到的字符串集合是所有后缀
3.如果该点$x$表示的不只一个字符串，那么把$x$复制一遍给$y$，这时$y$只表示一个字符串，相当于$x$表示的字符串集合中有一个串的$Endpos$和其余的不同了所以要把这个状态剥离给$y$，同时在$Parent$树上父亲指向$x$也要指向$y$

二、题单

• [hihocoder1441]后缀自动机一·基本概念 http://hihocoder.com/problemset/problem/1441
• [hihocoder1445]后缀自动机二·重复旋律5 http://hihocoder.com/problemset/problem/1445
• [hihocoder1449]后缀自动机三·重复旋律6 http://hihocoder.com/problemset/problem/1449
• [hihocoder1457]后缀自动机四·重复旋律7 http://hihocoder.com/problemset/problem/1457
• [hihocoder1465]后缀自动机五·重复旋律8 http://hihocoder.com/problemset/problem/1465
• [HihoCoder1413]Rikka with String
• [Luogu3804]【模板】后缀自动机 https://www.luogu.org/problemnew/show/P3804
• [BZOJ4516][SDOI2016]生成魔咒
• [BZOJ3998][TJOI2015]弦论 https://www.luogu.org/problemnew/show/P3975
• [BZOJ3277]串 https://www.lydsy.com/JudgeOnline/problem.php?id=3277
• [BZOJ3926][ZJOI2015]诸神眷顾的幻想乡
• [BZOJ2806][CTSC2012]熟悉的文章(Cheat) https://www.luogu.org/problemnew/show/P4022
• [BZOJ1396&2865]识别子串
• [HEOI2015]最短不公共子串 https://www.luogu.org/problemnew/show/P4112
• [BZOJ2555]SubString
• [BZOJ5137][Usaco2017 Dec]Standing Out from the Herd
• [BZOJ2780][SPOJ8093]Sevenk Love Oimaster https://www.luogu.org/problemnew/show/SP8093
• [CF700E]Cool Slogans https://www.luogu.org/problemnew/show/CF700E
• [CF666E]Forensic Examination
• [BZOJ5408][HN省队集训6.25T3]string https://www.lydsy.com/JudgeOnline/problem.php?id=5408

三、一句话题解

四、模板

洛谷 P3804 【模板】后缀自动机

// luogu-judger-enable-o2
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#define ll long long
using namespace std;
const int N=2010000;
char s[N];
int fa[N],ch[N][26],len[N],siz[N];
int lst=1,node=1,l,t[N],A[N];
ll ans;
void Extend(int c)
{
    /*
      如果是广义后缀自动机的话，最好加上第一句，虽然不加不会错
      这句的意思是要加入的这个点已经存在（Trie树上的同一个点再次被访问）
      不加就相当把这个点作为中转站，但是又和Situation2那个错误的中转站不同，这个没有被parent父亲指，所以不会被魔改
    */
    if(ch[lst][c]&&len[ch[lst][c]]==len[lst]+1) {lst=ch[lst][c];siz[lst]++;return;}
    /*
      2+2+2+3行，那么多while但是复杂度是O(n)
     */
    int f=lst,p=++node;lst=p;
    len[p]=len[f]+1;siz[p]=1;
    /*
      f为以c结尾的前缀的倒数第二个节点，p为倒数第一个（新建）
      len[i] 表示i节点的longest，不用记录shortest（概念在hihocoder后缀自动机1上讲得十分详细）
      siz[i]表示以i所代表的endpos的集合元素大小，即所对应的字符串集出现的次数
      不用担心复制后的siz，在parent树上复制后的点的siz是它所有儿子siz之和，比1多
     */
    while(f&&!ch[f][c]) ch[f][c]=p,f=fa[f];
    if(!f) {fa[p]=1;return;}
    /*
      把前面的一段没有c儿子的节点的c儿子指向p
      Situation 1 如果跳到最前面的根的时候，那么把p的parent树上的父亲置为1
     */
    int x=ch[f][c],y=++node;
    if(len[f]+1==len[x]) {fa[p]=x;node--;return;}
    /*
      x表示从p一直跳parent树得到的第一个有c儿子的节点的c儿子
      Situation 2 如果节点x表示的endpos所对应的字符串集合只有一个字符串，那么把p的parent树父亲设置为x
     */
    len[y]=len[f]+1; fa[y]=fa[x]; fa[x]=fa[p]=y;
    memcpy(ch[y],ch[x],sizeof(ch[y]));
    while(f&&ch[f][c]==x) ch[f][c]=y,f=fa[f];
    /*
      Situation 3 否则把x点复制一遍（parent树父亲、儿子），同时len要更新
                 （注意len[x]!=len[f]+1,因为通过加点会使x父亲改变）
                  然后把x点和p点的父亲指向复制点y，再将前面所有本连x的点连向y
     */
}
int main()
{
    //Part 1 建立后缀自动机
    scanf("%s",s); l=strlen(s);
    for(int i=l;i>=1;i--) s[i]=s[i-1];s[0]=0;
    for(int i=1;i<=l;i++) Extend(s[i]-'a');
    //Part 2 按len从大到小排序（和SA好像啊）后计算答案
    for(int i=1;i<=node;i++) t[len[i]]++;
    for(int i=1;i<=node;i++) t[i]+=t[i-1];
    for(int i=1;i<=node;i++) A[t[len[i]]--]=i;
    for(int i=node;i>=1;i--)
    {//从小到大枚举，实际上在模拟parent树的DFS
        int now=A[i];siz[fa[now]]+=siz[now];
        if(siz[now]>1) ans=max(ans,1ll*siz[now]*len[now]);
    }
    printf("%lld\n",ans);
    return 0;
}