HAOI2018 简要题解
HAOI2018 简要题解
R1T1 奇怪的背包
题意
小C非常擅长背包问题,他有一个奇怪的背包,这个背包有一个参数 \(P\) ,当他向这个背包内放入若干个物品后,背包的重量是物品总体积对 \(P\) 取模后的结果.
现在小C有 \(n\) 种体积不同的物品,第 \(i\) 种占用体积为 \(V_i\) ,每种物品都有无限个.他会进行 \(q\) 次询问,每次询问给出重量 \(w_i\) ,你需要回答有多少种放入物品的方案,能将一个初始为空的背包的重量变为 \(w_i\) .注意,两种方案被认为是不同的,当且仅当放入物品的种类不同,而与每种物品放入的个数无关.不难发现总的方案数为 \(2^n\) .
由于答案可能很大,你只需要输出答案对 \(10^9 + 7\) 取模的结果.

题解
这题耐着性子打:测试1、7是人口普查,测试234暴力枚举选或不选DP转移
可以发现一个性质:\(V[i]=gcd(V[i],P)\)
然后如果选的集合是S,则需要\(gcd(V[i],P)(i\in S)|gcd(w,P)\),才能满足条件。这个瞪了好久没有瞪出来。
原理是这样的:如果选了两个\(V[i],V[j]\)(已经对P取了\(gcd\)),那么可以表示\(P-V[i]+V[j]\),也就是说,可以当做多选了一个\(V[j]-V[i]\),同理这样可以找到\(gcd(V[i],V[j])\)。
有一个结论:两亿以内,约数最多的数的约数个数为1536。所以给P的约数编个号,设\(dp[i][j]\)表示在前面\(i\)个数中、选出的数的\(gcd\)为第\(j\)个约数,的选数的方案数。最后统计\(Ans[i]\)表示\(gcd(P,w)=\)第i个约数 的对应\(w\)的答案。
代码
直接看Work5就好了。
#include<iostream>
#include<queue>
#include<cstring>
#include<map>
#include<algorithm>
using namespace std;
int read()
{
char ch=getchar();int h=0;
while(ch>'9'||ch<'0') ch=getchar();
while(ch>='0'&&ch<='9') h=h*10+ch-'0',ch=getchar();
return h;
}
int gcd(int a,int b) {return b?gcd(b,a%b):a;}
const int N=1e6+10,mod=1e9+7;
int n,q,P,V[N],w[N],bit[N];
void Work1()
{
int d=gcd(V[1],P),x;
while(q--) x=read(),printf("%d\n",x%d==0?1:0);
exit(0);
}
void Work2()
{
for(int i=1;i<=q;i++)
printf("%d\n",(bit[n]+mod-1)%mod);
exit(0);
}
void Work3()
{
queue<int> Q;
int f[300],ans[300],to[20],tt=0;
memset(ans,0,sizeof(ans));
memset(f,0,sizeof(f));
for(int zt=0;zt<1<<n;zt++)
{
tt=0;
for(int i=1;i<=n;i++)
if(((1<<(i-1))&zt)&&f[V[i]]!=zt)
f[V[i]]=zt,Q.push(V[i]),to[++tt]=V[i];
while(!Q.empty())
{
int x=Q.front();Q.pop();ans[x]++;
for(int i=1;i<=tt;i++)
if(f[(x+to[i])%P]!=zt) f[(x+to[i])%P]=zt,Q.push((x+to[i])%P);
}
}
for(int i=1,x;i<=q;i++)
x=read(),printf("%d\n",ans[x]);
exit(0);
}
int dp[1001][10010];
void Work4()
{
dp[0][0]=1;
for(int i=1;i<=n;i++)
{
for(int j=0;j<P;j++) dp[i][j]=dp[i-1][j];
for(int j=0;j<P;j++)
(dp[i][gcd(V[i],j)]+=dp[i-1][j])%=mod;
}
for(int i=1,x,ans;i<=q;i++)
{
x=read();ans=0;
for(int j=1;j*j<=x;j++)
if(x%j==0)
{
(ans+=dp[n][j])%=mod;
if(j*j!=x) (ans+=dp[n][x/j])%=mod;
}
printf("%d\n",ans);
}
exit(0);
}
int f[2000][2000],Ans[2000];
int W[2000],cof[2000],id[2000];
map<int,int> to;
void Work5()
{
int tt=0,u=0;
f[0][0]=1;to[0]=0;
for(int i=1;i*i<=P;i++)
if(P%i==0)
{
to[i]=++tt;id[tt]=i;
if(i*i!=P) to[P/i]=++tt,id[tt]=P/i;
}
sort(V+1,V+n+1);
for(int i=1;i<=n;i++)
if(V[i]!=V[i-1]) W[++u]=V[i],cof[u]=1;
else cof[u]++;
for(int i=1;i<=u;i++) cof[i]=bit[cof[i]]-1;
for(int i=1;i<=u;i++)
{
for(int j=0;j<=tt;j++) f[i][j]=f[i-1][j];
for(int j=0;j<=tt;j++)
(f[i][to[gcd(id[j],W[i])]]+=1ll*cof[i]*f[i-1][j]%mod)%=mod;
}
for(int i=1,x,ans;i<=tt;i++)
{
x=id[i];ans=0;
for(int j=1;j<=tt;j++)
if(x%id[j]==0) (ans+=f[u][j])%=mod;
Ans[i]=ans;
}
for(int i=1,x;i<=q;i++)
x=gcd(read(),P),printf("%d\n",Ans[to[x]]);
}
int main()
{
cin>>n>>q>>P;
bit[0]=1;
for(int i=1;i<=n;i++) V[i]=read(),V[i]=gcd(V[i],P);
for(int i=1;i<=n;i++) bit[i]=2ll*bit[i-1]%mod;
if(n==1) Work1();
if(P==998244353) Work2();
if(P<=250&&n<=10) Work3();
if(P<=10000) Work4();
Work5();
}
R1T2反色游戏
题意
小C和小G经常在一起研究搏弈论问题,有一天他们想到了这样一个游戏.
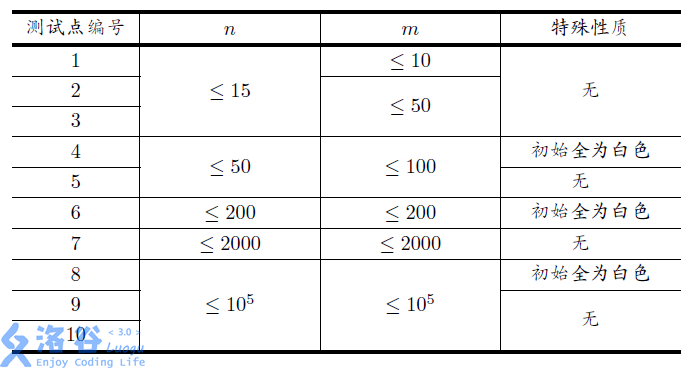
有一个 \(n\) 个点 \(m\) 条边的无向图,初始时每个节点有一个颜色,要么是黑色,要么是白色.现在他们对于每条边做出一次抉择:要么将这条边连接的两个节点都反色(黑变白,白变黑),要么不作处理.他们想把所有节点都变为白色,他们想知道在 \(2^m\) 种决策中,有多少种方案能达成这个目标.
小G认为这个问题太水了,于是他还想知道,对于第 \(i\) 个点,在删去这个点及与它相连的边后,新的答案是多少.
由于答案可能很大,你只需要输出答案对 \(10^9 + 7\) 取模后的结果.
题解
耐着性子打30分暴力。
对于这种翻转颜色,可以想到异或方程组,然后答案就是\(2^{自由元}\)。但是由于询问过多,不会动态维护,只能GG。
考虑正解:对于一个联通块来说,如果构成一棵树,那么方案唯一;如果不是一棵树,对于\(m-n+1\)条非树边,可以选也可以不选,选了就对应选树上路径使得没有影响,方案数为\(2^{m-n+1}\)。
如果有一个联通块有奇数个黑点,那么答案为0;否则答案为\(2^{m-n+cc}\),\(cc\)为联通块个数。
怎么去删点呢?我们发现只有割点影响联通块划分,于是删去点\(i\)需要考虑以下情况:
- \(i\)度数为0,自成一个联通块
- \(i\)不是割点,需要看联通块的黑点数的奇偶性
- \(i\)是割点,需要看被划分出来的各个联通块的黑点数是否存在奇数
全部用Tarjan实现。具体实现细节有点多,看代码好了。
代码
#include<iostream>
#include<cstring>
#include<bitset>
using namespace std;
const int N=1e5+10,mod=1e9+7;
struct Edge{int fr,to;}E[N];
int n,m;
char s[N];
namespace cpp1
{
int dp[51][1<<15],bit[20],tag[51];
void Calc()
{
memset(dp,0,sizeof(dp));
int start=0;
for(int i=1;i<=n;i++) start|=bit[i]*(s[i]-'0');
dp[0][start]=1;
for(int i=1;i<=m;i++)
for(int zt=0;zt<bit[n+1];zt++)
{
dp[i][zt]=dp[i-1][zt];
if(!tag[i]) (dp[i][zt]+=dp[i-1][zt^bit[E[i].fr]^bit[E[i].to]])%=mod;
}
printf("%d ",dp[m][0]);
}
void main()
{
for(int i=1;i<=n+1;i++) bit[i]=1<<(i-1);
Calc();
for(int i=1;i<=n;i++)
{
char tmp=s[i];s[i]='0';
for(int j=1;j<=m;j++)
if(E[j].fr==i||E[j].to==i) tag[j]=1;
Calc();s[i]=tmp;
for(int j=1;j<=m;j++) tag[j]=0;
}
puts("");
}
}
namespace cpp2
{
struct edge{int next,to;}a[N<<1];
int tag[N],dfn[N],low[N],tot,head[N],cnt,g[N];
int vis[N],siz[N],cc,ww,d[N],du[N],bit[N<<1];
void link(int x,int y)
{
du[x]++;du[y]++;
a[++cnt]=(edge){head[x],y};head[x]=cnt;
a[++cnt]=(edge){head[y],x};head[y]=cnt;
}
void Min(int &x,int y) {if(y<x) x=y;}
void Tarjan(int x,int fr,int rt)
{
int ss=0;dfn[x]=low[x]=++tot;
siz[x]=(s[x]=='1');vis[x]=rt;
for(int i=head[x];i;i=a[i].next)
{
int R=a[i].to;if(R==fr) continue;
if(!dfn[R])
{
Tarjan(R,x,rt);siz[x]+=siz[R];
ss++;Min(low[x],low[R]);
if(low[R]>=dfn[x]) tag[x]++,d[x]|=siz[R]&1,g[x]+=siz[R];
}
else Min(low[x],dfn[R]);
}
if(!fr) tag[x]--;
}
void main()
{
memset(head,0,sizeof(head));
memset(vis,0,sizeof(vis));
memset(dfn,0,sizeof(dfn));
memset(d,0,sizeof(d));
memset(g,0,sizeof(g));
memset(tag,0,sizeof(tag));
memset(du,0,sizeof(du));
bit[0]=1;cnt=tot=cc=ww=0;
for(int i=1;i<=m;i++) link(E[i].fr,E[i].to);
for(int i=1;i<=n;i++)
if(!dfn[i]) cc++,Tarjan(i,0,i),ww+=(siz[i]&1);
for(int i=1;i<=m*2;i++) bit[i]=bit[i-1]*2ll%mod;
printf("%d ",ww?0:bit[m-n+cc]);
for(int i=1;i<=n;i++)
if(ww-(siz[vis[i]]&1)) printf("0 ");
else if(d[i]) printf("0 ");
else if((siz[vis[i]]-(s[i]=='1')-g[i])&1) printf("0 ");
else printf("%d ",bit[m-n+cc+tag[i]+1-du[i]]);
puts("");
}
}
void Work()
{
cin>>n>>m;
for(int i=1;i<=m;i++) scanf("%d%d",&E[i].fr,&E[i].to);
scanf("%s",s+1);
if(n<=15&&m<=50) cpp1::main();
else cpp2::main();
}
int main() {int T;cin>>T;while(T--) Work();}
R1T3 字串覆盖
题意
小C对字符串颇有研究,他觉得传统的字符串匹配太无聊了,于是他想到了这样一个问题.
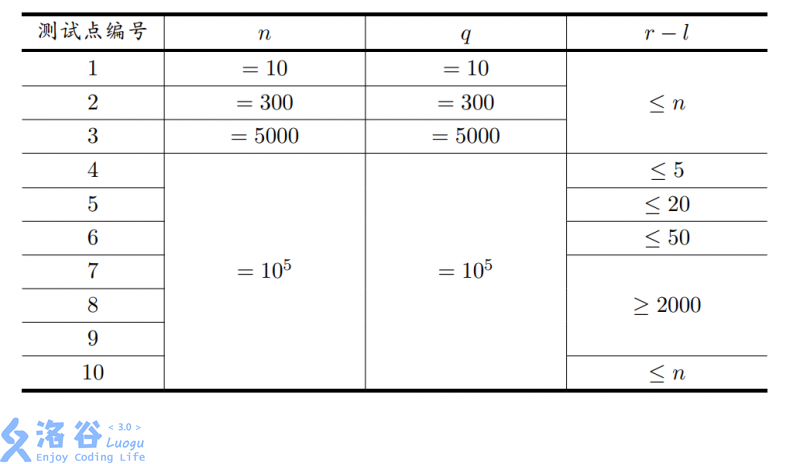
对于两个长度为 \(n\) 的串 \(A, B\) , 小C每次会给出给出 \(4\) 个参数 \(s, t, l, r\) . 令 \(A\) 从 \(s\) 到 \(t\) 的子串(从 \(1\) 开始标号)为 \(T\),令 \(B\) 从 \(l\) 到 \(r\) 的子串为 \(P\).然后他会进行下面的操作:
如果 \(T\) 的某个子串与 \(P\) 相同,我们就可以覆盖 \(T\) 的这个子串,并获得 \(K - i\) 的收益,其中 \(i\) 是初始时 \(A\) 中(注意不是 \(T\) 中)这个子串的起始位置,\(K\)是给定的参数.一个位置不能被覆盖多次.覆盖操作可以进行任意多次,你需要输出获得收益的最大值.
注意每次询问都是独立的,即进行一次询问后,覆盖的位置会复原.
题解
暴力30分,眼刷了。再没思路。
但是题目提示得很明显:按照\(l\)的大小分别做。
orz出题人:https://dy0607.github.io/省选/oi历程/2018/04/24/HAOI2018-Round1-解题报告.html
对于询问串长>50的串:
答案会很小,于是可以暴力一个一个加答案,过程如下:
- 求出SA数组,倍增出该询问的左右端点(也就是排名为\([l,r]\)间的串的lcp大于询问串长)。
- 查位置在\([s,t]\)(也就是给你的母串)中、排名在\([l,r]\)的位置最小的点,累加答案。
对于询问串长<=50的串:
对每种长度的询问串分别计算,把每个点向右边第一个表示串相同、不相交的点连边。连成一个森林结构,倍增统计答案即可。
代码
#include<iostream>
#include<cstring>
#include<algorithm>
#define ll long long
#define log2 caijixzy
using namespace std;
const int N=3e5+10;
int n,K;
char S[N],s[N];
//Part 1 Get SA
int l,SA[N],rk[N],x[N],y[N],t[N],m,h[N];
int cmp(int i,int j,int k) {return y[i]==y[j]&&y[i+k]==y[j+k];}
void Sort()
{
for(int i=1;i<=m;i++) t[i]=0;
for(int i=1;i<=l;i++) t[x[i]]++;
for(int i=1;i<=m;i++) t[i]+=t[i-1];
for(int i=l;i>=1;i--) SA[t[x[y[i]]]--]=y[i];
}
void GetSA()
{
m=1000;l=n*2+1;
for(int i=1;i<=l;i++) x[i]=s[i],y[i]=i;Sort();
for(int k=1,p=0;k<=l;k<<=1)
{
for(int i=l-k+1;i<=l;i++) y[++p]=i;
for(int i=1;i<=l;i++) if(SA[i]>k) y[++p]=SA[i]-k;
Sort();swap(x,y);x[SA[1]]=p=1;
for(int i=2;i<=l;i++) x[SA[i]]=cmp(SA[i],SA[i-1],k)?p:++p;
if(p==l) break;m=p,p=0;
}
for(int i=1;i<=l;i++) rk[SA[i]]=i;
for(int i=1,j=0;i<=l;i++)
{
while(s[i+j]==s[SA[rk[i]-1]+j]) j++;
h[rk[i]]=j;if(j) j--;
}
}
//Part 2 Get answers <=50
struct Que{int s,t,l,len,id,pos;}Q[N];
int q,pos[N],log2[N],fa[N][20];
ll sum[N][20],Ans[N];
int cmp1(const Que&A,const Que&B) {return A.len==B.len?A.pos<B.pos:A.len<B.len;}
void Calc(int len,int &it)
{
if(Q[it].len!=len) return;
for(int l=1,r=1,cc=0;l<=2*n+1;r=l=r+1,cc=0)
{
while(h[r]>=len) ++r;
for(int i=l;i<=r;i++) if(SA[i]<=n) pos[++cc]=SA[i];
if(Q[it].pos>r||Q[it].pos<l) continue;
sort(pos+1,pos+cc+1);pos[cc+1]=2*n+2;
int up=log2[min(n/len,cc)],k=1;
for(int i=1;i<=cc;i++)
{
while(pos[k]-pos[i]<len) k++;
fa[i][0]=k;sum[i][0]=K-pos[i];
}
for(int p=1;p<=up;p++)
for(int i=1;i<=cc;i++)
if(fa[fa[i][p-1]][p-1])
{
fa[i][p]=fa[fa[i][p-1]][p-1];
sum[i][p]=sum[i][p-1]+sum[fa[i][p-1]][p-1];
}
for(ll res=0;Q[it].len==len&&Q[it].pos<=r;it++,res=0)
{
int s=Q[it].s,t=Q[it].t,x=lower_bound(pos+1,pos+cc+2,s)-pos;
if(pos[x]>t) continue;
for(int p=up;p>=0;p--)
if(pos[fa[x][p]]<=t&&pos[fa[x][p]])
res+=sum[x][p],x=fa[x][p];
Ans[Q[it].id]=res+sum[x][0];
}
for(int i=1;i<=cc;i++)
for(int p=0;p<=up;p++) fa[i][p]=0,sum[i][p]=0;
}
}
//Part 3 Get answers >50
int ST[N][20],rt[N],nod;
struct President_Tree
{
#define lc t[x].ch[0]
#define rc t[x].ch[1]
struct seg{int ch[2],siz;}t[N*30];
void Add(int &x,int l,int r,int p)
{
t[++nod]=t[x];t[x=nod].siz++;
if(l==r) return;
int mid=(l+r)>>1;
if(p<=mid) Add(lc,l,mid,p);
else Add(rc,mid+1,r,p);
}
int Query(int R,int L,int l,int r,int p)
{
if(t[R].siz-t[L].siz==0) return 0;
if(l==r) return l;
int mid=(l+r)>>1,res=0;
int sizl=t[t[R].ch[0]].siz-t[t[L].ch[0]].siz;
if(p<=mid&&sizl) res=Query(t[R].ch[0],t[L].ch[0],l,mid,p);
if(!res) res=Query(t[R].ch[1],t[L].ch[1],mid+1,r,p);
return res;
}
}T;
int main()
{
//Part 1 Init and build sa
cin>>n>>K;
scanf("%s%s",s+1,S+1);s[n+1]='#';
for(int i=n+2;i<=n+n+1;i++) s[i]=S[i-n-1];
GetSA();cin>>q;
for(int i=1;i<=n*2+1;i++) h[i]=h[i+1];
for(int i=1;i<=q;i++)
{
int s,t,l,r;scanf("%d%d%d%d",&s,&t,&l,&r);
Q[i]=(Que){s,t-(r-l),l,r-l+1,i,rk[l+n+1]};
}
//Part 2 Get answers <=50
int it=1;
log2[1]=0;
for(int i=1;i<=n*2+1;i++) log2[i]=log2[i>>1]+1;
sort(Q+1,Q+q+1,cmp1);
for(int i=1;i<=min(n,50);i++) Calc(i,it);
//Part 3 Get answers >50
for(int i=1;i<=n*2+1;i++) ST[i][0]=h[i];
for(int p=1;p<=log2[2*n+1];p++)
for(int i=1;i<=n*2+1;i++)
ST[i][p]=min(ST[i][p-1],ST[i+(1<<(p-1))][p-1]);
for(int i=1;i<=n*2+1;i++)
{
rt[i]=rt[i-1];
if(SA[i]<=n) T.Add(rt[i],1,n,SA[i]);
}
for(;it<=q;it++)
{
int l,r;l=r=Q[it].pos;
for(int p=log2[n];p>=0;p--)
if(l-(1<<p)>=1&&ST[l-(1<<p)][p]>=Q[it].len) l=l-(1<<p);
for(int p=log2[n];p>=0;p--)
if(r+(1<<p)<=n*2+1&&ST[r][p]>=Q[it].len) r=r+(1<<p);
for(int p=Q[it].s;p<=Q[it].t;)
{
int nw=T.Query(rt[r],rt[l-1],1,n,p);
if(nw>Q[it].t||!nw) break;
Ans[Q[it].id]+=K-nw;
p=nw+Q[it].len;
}
}
for(int i=1;i<=q;i++) printf("%lld\n",Ans[i]);
return 0;
}
R2T1 苹果树
题意
小C在自己家的花园里种了一棵苹果树,树上每个结点都有恰好两个分支。经过细心的观察,小C发现每一天这棵树都会生长出一个新的结点。
第一天的时候, 果树会长出一个根结点,以后每一天,果树会随机选择一个当前树中没有长出过结点的分支,
然后在这个分支上长出一个新结点,新结点与分支所属的结点之间连接上一条边。
小C定义一棵果树的不便度为树上两两结点之间的距离之和,两个结点之间的距离定义为从一个点走到另一个点的路径经过的边数。
现在他非常好奇,如果 \(N\) 天之后小G来他家摘苹果,这个不便度的期望 \(E\) 是多少。但是小C讨厌分数,,所以他只想知道 \(E \times N!\) 对 \(P\) 取模的结果,可以证明这是一个整数。
对于 \(20\%\) 的数据,\(N \le 10\);
对于 \(50\%\) 的数据,\(N \le 500\);
对于另外 \(20\%\) 的数据,\(P = 10^9 + 7\);
对于 \(100\%\) 的数据,\(N \le 2000, P \le 10^9 + 7\)。
题解
题意就是所有二叉树的答案之和。
转而考虑每条边(每个点向父亲连边)的贡献:
点对数:\(siz_i*(n-siz_i)\)
给定\(t=siz_i\),此时的树的生成方式:\(i!C_{n-i}^{siz_i}siz_i!(i-2)(i-1)i(i+1)...(i-2+n-i-siz_i+1)\)
解释一下树的生成方式:
- 对于前\(i\)个点的生成方式,显然是\(i!\)
- 在接下来的\(n-i\)个点中,选择\(siz_i\)个点放进\(i\)的子树,方案是\(siz_i!\)
- 剩下的\(n-i-siz_i\)个点放在子树外面,可放位置为上述上升幂
所以枚举每一条边这么算就好了。
代码
#include<iostream>
#include<cstdio>
#include<cstdlib>
using namespace std;
const int N=2010;
int n,p,jc[N],C[N][N],ans;
int main()
{
cin>>n>>p;jc[0]=C[0][0]=1;
for(int i=1;i<=n;i++) jc[i]=1ll*jc[i-1]*i%p,C[i][0]=1;
for(int i=1;i<=n;i++)
for(int j=1;j<=i;j++)
C[i][j]=(C[i-1][j-1]+C[i-1][j])%p;
for(int i=2;i<=n;i++)
for(int j=1;j<=n-i+1;j++)
{
int bs=1ll*j*(n-j)%p;
int res=1ll*i*(i-1)%p*jc[n-j-1]%p;
(ans+=1ll*C[n-i][j-1]*jc[j]%p*res%p*bs%p)%=p;
}
cout<<ans<<endl;
}
R2T2 染色
题意
为了报答小 C 的苹果, 小 G 打算送给热爱美术的小 C 一块画布,
这块画布可以抽象为一个长度为 \(N\) 的序列, 每个位置都可以被染成 \(M\) 种颜色中的某一种.
然而小 C 只关心序列的 \(N\) 个位置中出现次数恰好为 \(S\) 的颜色种数,
如果恰好出现了 \(S\) 次的颜色有 \(K\) 种, 则小C会产生 \(W_k\) 的愉悦度.
小 C 希望知道对于所有可能的染色方案, 他能获得的愉悦度的和对 \(1004535809\) 取模的结果是多少.
对于 \(10\%\) 的数据,\(N \le 10, M \le 5\);
对于 \(30\%\) 的数据,\(N \le 100, M \le 100\);
对于另外 \(10\%\) 的数据,$ M \le 1000$;
对于另外 \(10\%\) 的数据,$ \forall 1 \le i \le M, W_i = 0$;
对于 \(100\%\) 的数据,\(N \le 10^7, M \le 10^5, S \le 150, 0 \le W_i < 1004535809\)。
题解
肯定要枚举k,于是有kS个位置是要染成同一种颜色。
得到式子:\(C(N,kS)*M*(M-1)^{N-kS}\),这显然计算的是至少为k的方案。
正好就是\(\sum_{j=k}^{lim}(-1)^{j-k}C(N,jS)*M*(M-1)^{N-jS}\),然后把式子拆开就可以直接NTT了。
代码
#include<iostream>
#include<algorithm>
using namespace std;
const int N=6e5+10,mod=1004535809,up=1e7;
int n,m,s,A[N],B[N],jc[up+10],inv[up+10];
int f[N],l,W[N],ans,tt,r[N],w[N];
int ksm(int x,int k)
{
int s=1;for(;k;k>>=1,x=1ll*x*x%mod)
if(k&1) s=1ll*s*x%mod;return s;
}
void NTT(int *P,int op)
{
for(int i=0;i<l;i++) if(i<r[i]) swap(P[i],P[r[i]]);
for(int i=1;i<l;i<<=1)
{
int W=ksm(3,(mod-1)/(i<<1));
if(op<0) W=ksm(W,mod-2);w[0]=1;
for(int j=1;j<i;j++) w[j]=1ll*w[j-1]*W%mod;
for(int j=0,p=i<<1;j<l;j+=p)
for(int k=0;k<i;k++)
{
int X=P[j+k],Y=1ll*P[j+k+i]*w[k]%mod;
P[j+k]=(X+Y)%mod;P[j+k+i]=(mod+(X-Y)%mod)%mod;
}
}
if(op<0) for(int inv=ksm(l,mod-2),i=0;i<l;i++) P[i]=1ll*P[i]*inv%mod;
}
int C(int n,int k) {return 1ll*jc[n]*inv[k]%mod*inv[n-k]%mod;}
int main()
{
cin>>n>>m>>s;
for(int i=0;i<=m;i++) cin>>W[i];
jc[0]=inv[0]=1;
for(int i=1;i<=up;i++) jc[i]=1ll*i*jc[i-1]%mod;
inv[up]=ksm(jc[up],mod-2);
for(int i=up-1;i>=1;i--) inv[i]=1ll*inv[i+1]*(i+1)%mod;
int lim=min(m,n/s);
for(int i=0,bs=1;i<=lim;i++,bs=1ll*bs*inv[s]%mod)
f[i]=1ll*C(m,i)%mod*C(n,i*s)%mod*bs%mod
*jc[i*s]%mod*ksm(m-i,n-i*s)%mod;
for(int i=0;i<=lim;i++)
A[i]=1ll*jc[i]*f[i]%mod,B[i]=(i&1)?mod-inv[i]:inv[i];
reverse(B+0,B+lim+1);
for(l=1;l<=lim*2;l<<=1) tt++;tt--;
for(int i=0;i<l;i++) r[i]=(r[i>>1]>>1)|((i&1)<<tt);
NTT(A,1);NTT(B,1);
for(int i=0;i<l;i++) A[i]=1ll*A[i]*B[i]%mod;
NTT(A,-1);
for(int i=0;i<=lim;i++) (ans+=1ll*A[lim+i]*inv[i]%mod*W[i]%mod)%=mod;
cout<<ans<<endl;
}
后记
orz dy&zjp_shadow!
题目质量相当高的!
当做模拟赛去打,结果是D1只有50+30+30,很凉了。
D2由于做过,所以假装AK了。。
这样的话和stdcall分数一样了
!!但是:D2没做过呢?D1时间只给三个半小时呢?那不切T1还有戏吗?凉了!
所以说HAOI2018这场我进不了队。


