CQOI2018简要题解

CQOI2018简要题解

D1T1 破解 D-H 协议

题意

Diffie-Hellman 密钥交换协议是一种简单有效的密钥交换方法。它可以让通讯双方在没有事先约定密钥（密码）的情况下，通过不安全的信道（可能被窃听）建立一个安全的密钥 \(K\)，用于加密之后的通讯内容。

假定通讯双方名为 Alice 和 Bob，协议的工作过程描述如下（其中 \(\bmod\) 表示取模运算）：

1. 协议规定一个固定的质数 \(P\)，以及模 \(P\) 的一个原根 \(g\)。\(P\) 和 \(g\) 的数值都是公开的，无需保密。
2. Alice 生成一个随机数 \(a\)，并计算 \(A=g^a\bmod P\)，将 \(A\) 通过不安全信道发送给 Bob。
3. Bob 生成一个随机数 \(b\)，并计算 \(B=g^b\bmod P\)，将 \(B\) 通过不安全信道发送给 Alice。
4. Bob 根据收到的 \(A\) 计算出 \(K=A^b\bmod P\)，而 Alice 根据收到的 \(B\) 计算出 \(K=B^a\bmod P\)。
5. 双方得到了相同的 \(K\)，即 \(g^{ab}\bmod P\)。\(K\) 可以用于之后通讯的加密密钥。

可见，这个过程中可能被窃听的只有 \(A,B\)，而 \(a,b,K\) 是保密的。并且根据 \(A,B,P,g\) 这 \(4\) 个数，不能轻易计算出 \(K\)，因此 \(K\) 可以作为一个安全的密钥。

当然安全是相对的，该协议的安全性取决于数值的大小，通常 \(a,b,P\) 都选取数百位以上的大整数以避免被破解。然而如果 Alice 和 Bob 编程时偷懒，为了避免实现大数运算，选择的数值都小于 \(2^{31}\)，那么破解他们的密钥就比较容易了。

第一行包含两个空格分开的正整数 \(g\) 和 \(P\)。

第二行为一个正整数 \(n\)，表示 Alice 和 Bob 共进行了 \(n\) 次连接（即运行了 \(n\) 次协议）。

接下来 \(n\) 行，每行包含两个空格分开的正整数 \(A\) 和 \(B\)，表示某次连接中，被窃听的 \(A,B\) 数值。

题解

BSGS裸题。

代码

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
using namespace std;
const int Mo=100003;
int a,b,A,B,P,n;
struct HashTable
{
	struct Line{int next,v1,v2;}a[Mo];
	int head[Mo],cnt;
	void reset() {memset(head,0,sizeof(head));cnt=0;}
	void Add(int p,int v1,int v2) {a[++cnt]=(Line){head[p],v1,v2};head[p]=cnt;}
	int Query(int x)
		{
			for(int i=head[x%Mo];i;i=a[i].next)
				if(a[i].v1==x) return a[i].v2;return -1;
		}
}Hash;
int ksm(int x,int k)
{
	int s=1;for(;k;k>>=1,x=1ll*x*x%P)
				if(k&1) s=1ll*s*x%P;return s;
}
int BSGS(int A,int B,int P)
{
	int M=sqrt(P)+1;Hash.reset();
	for(int i=0,t=B;i<M;i++,t=1ll*t*A%P) Hash.Add(t%Mo,t,i);
	for(int i=1,bs=ksm(A,M),t=bs;i<=M;i++,t=1ll*t*bs%P)
		if(Hash.Query(t)!=-1) return i*M-Hash.Query(t);return -1;
}
int main()
{
	cin>>A>>P>>n;
	while(n--)
	{
		cin>>B>>b;a=BSGS(A,B,P);
		printf("%d\n",ksm(b,a));
	}
	return 0;
}

D1T2 社交网络

题意

当今社会，在社交网络上看朋友的消息已经成为许多人生活的一部分。通常，一个用户在社交网络上发布一条消息（例如微博、状态、Tweet 等）后，他的好友们也可以看见这条消息，并可能转发。转发的消息还可以继续被人转发，进而扩散到整个社交网络中。

在一个实验性的小规模社交网络中我们发现，有时一条热门消息最终会被所有人转发。为了研究这一现象发生的过程，我们希望计算一条消息所有可能的转发途径有多少种。为了编程方便，我们将初始消息发送者编号为 \(1\)，其他用户编号依次递增。

该社交网络上的所有好友关系是已知的，也就是说对于 A、B 两个用户，我们知道 A 用户可以看到 B 用户发送的消息。注意可能存在单向的好友关系，即 A 能看到 B 的消息，但 B 不能看到 A 的消息。

还有一个假设是，如果某用户看到他的多个好友转发了同一条消息，他只会选择从其中一个转发，最多转发一次消息。从不同好友的转发，被视为不同的情况。

如果用箭头表示好友关系，下图展示了某个社交网络中消息转发的所有可能情况。（初始消息是用户 \(1\) 发送的，加粗箭头表示一次消息转发）

对于 \(30\%\) 的数据，\(1≤n≤10\)。

对于 \(100\%\) 的数据，\(1\leq n\leq 250, 1\leq a_i,b_i\leq n, 1\leq m\leq n(n-1)\)。

题解

矩阵树定理裸题。

对于有向图有根树的计数，边\(x->y\)则矩阵\(a[x][y]--,a[y][y]++\)，即度数矩阵为入读。同时注意删去根所在的那一行一列。

代码

#include<iostream>
using namespace std;
const int P=10007;
int n,m,g[251][251],ans=1;
int main()
{
	cin>>n>>m;
	for(int i=1,a,b;i<=m;i++)
	{
		scanf("%d%d",&b,&a);
		g[a][b]--;g[b][b]++;
	}
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			(g[i][j]+=P)%=P;
	for(int i=2;i<=n;i++)
		for(int j=i+1;j<=n;j++)
			while(g[j][i])
			{
				int t=g[i][i]/g[j][i];ans=-ans;
				for(int k=i;k<=n;k++)
					g[i][k]=(P+g[i][k]-1ll*t*g[j][k]%P)%P,swap(g[i][k],g[j][k]);
			}
	for(int i=2;i<=n;i++) ans=1ll*ans*g[i][i]%P;
	cout<<(ans+P)%P<<endl;
}

D1T3 交错序列

题意

我们称一个仅由 \(0,1\) 构成的序列为「交错序列」，当且仅当序列中没有相邻的 \(1\)（可以有相邻的 \(0\)）。例如，\(000,001,101\) 都是交错序列，而 \(110\) 则不是。

对于一个长度为 \(n\) 的交错序列，统计其中 \(0\) 和 \(1\) 出现的次数，分别记为 \(x\) 和 \(y\)。给定参数 \(a,b\)，定义一个交错序列的特征值为 \(x^ay^b\)。注意这里规定任何整数的 \(0\) 次幂都等于 \(1\)（包括 \(0^0=1\)）。

显然长度为 \(n\) 的交错序列可能有多个。我们想要知道，所有长度为 \(n\) 的交错序列的特征值的和，除以 \(m\) 的余数。（\(m\) 是一个给定的质数）

例如，全部长度为 \(3\) 的交错串为：\(000,001,010,100,101\)。当 \(a=1,b=2\) 时，可计算：\(3^1\times0^2+2^1\times1^2+2^1\times1^2+2^1\times1^2+1^1\times2^2=10\)。

对于 \(30\%\) 的数据，\(1\leq n\leq 15\)。

对于 \(100\%\) 的数据，\(1\leq n\leq 10^7,0\leq a,b\leq 45, m<10^8\)。

题解

唯一一道有点意思的题目。

首先考虑\(\mathcal O(nlog)\)暴力：枚举\(1\)有多少个，此时0的方案数可以直接用组合数算：\(C(n+1-i,i)\)。有\(i\)个1，那么有\(n-i\)个0，我们可以在这\(n-i\)个位置以及第0个位置、一共\(n+1-i\)个位置中，选择\(i\)个位置在后面放1。

所以答案是\(\sum_{i=0}^{\lfloor \frac{n+1}{2}\rfloor} C_{n+i-1}^{i}(n-i)^ai^b\)。

然而这只有暴力的三十分，由于数据范围极具误导性，卡了半个小时常仍然无果（甚至试了线性筛快速幂）。

正解是这样的：用二项式定理拆开式子

\[x^ay^b=(n-y)^ay^b=\sum_{i=0}^aC_a^in^i(-y)^{a-i}y^b=\sum_{i=0}^a(-1)^{a-i}C_a^in^iy^{a+b-i} \]

现在考虑的就是\(y\)的所有方案的幂次和是什么，或者根据刚才的式子，可以得到

\[Ans=\sum_{y=0}^{\lfloor \frac{n+1}{2}\rfloor}C_{n+y-1}^y(n-y)^ay^b=\sum_{i=0}^{a}(-1)^{a-i}C_a^in^i\sum_{y=0}^{\lfloor \frac{n+1}{2}\rfloor}y^{a+b-i}C_{n+1-y}^y \]

现在我们要求算\(f[k]\)表示后面那个\(\sum\)中\(a+b-i=k\)时候的和。

令\(f[k][i][0/1]\)表示长度为\(k\)的序列，后面那一坨指数是\(i\)的和。

有转移：

\[f[k][i][0]=f[k-1][i][0]+f[k-1][i][1] \]

表示在末尾接一个0，可以从1和0同时转移。

\[f[k][i][1]=\sum_{j=0}^i C_i^jf[k-1][i][0] \]

表示在末尾接一个1，相当于给\(y\)+1，二项式展开后是这幅面孔。

然后由于k比较大，所以通过矩阵转移，这种多维DP的矩阵会分区，比如这题的矩阵如下构造：

• 答案矩阵，第\(1​\)_{$a+b+1​$行第$1$列表示$f[i][0]$；第$a+b+2$}\(2(a+b+1)\)第\(1\)列表示\(f[i][1]\)。
• \(1\)_{$a+b+1$行，$1$}\(a+b+1\)列，表示\(f[i][0]\)向\(f[i][0]\)的转移，即\(G[i][i]=1\)。
• \(1\)_{$a+b+1$行，$a+b+2$}\(2(a+b+1)\)列，表示\(f[i][1]\)向\(f[i][0]\)的转移，即\(G[i][i]=1\)。
• \(a+b+2\)_{$2(a+b+1)$行，$1$}\(a+b+1\)列，表示\(f[i][0]\)向\(f[i][1]\)的转移，为杨辉三角。
• \(a+b+2\)_{$2(a+b+1)$行，$a+b+2$}\(2(a+b+1)\)列，表示\(f[i][1]\)向\(f[i][1]\)的转移，全是\(0\)。

代码

#include<iostream>
#include<cstring>
using namespace std;
const int N=1e7+10;
int n,a,b,p,C[100][100],l,Ans;
struct matrix
{
	long long a[200][200];
	matrix () {memset(a,0,sizeof(a));}
	matrix operator * (matrix A)
		{
			matrix C;
			for(int i=1;i<=l;i++)
				for(int j=1;j<=l;j++)
				{
					for(int k=1;k<=l;k++)
						C.a[i][j]+=a[i][k]*A.a[k][j];
					C.a[i][j]%=p;
				}
			return C;
		}
}A,B;
int main()
{
	cin>>n>>a>>b>>p;
	for(int i=0;i<=99;i++) C[i][0]=1;
	for(int i=1;i<=99;i++)
		for(int j=1;j<=99;j++)
			C[i][j]=(C[i-1][j-1]+C[i-1][j])%p;
	l=(a+b+1)*2;
	for(int i=1;i<=l/2;i++)
	{
		A.a[i][i]=A.a[i][l/2+i]=1;
		for(int j=1;j<=i;j++)
			A.a[l/2+i][j]=C[i-1][j-1];
	}
	for(int i=1;i<=l;i++) B.a[i][i]=1;
	for(int k=n;k;k>>=1,A=A*A) if(k&1) B=B*A;
	for(int i=0,pw=1;i<=a;i++,pw=1ll*pw*n%p)
		(Ans+=1ll*(((a-i)&1)?-1:1)*C[a][i]*pw%p*(B.a[a+b-i+1][1]+B.a[l/2+a+b-i+1][1])%p)%=p;
	cout<<(Ans+p)%p;
}

D2T1 解锁屏幕

题意

使用过 Android 手机的同学一定对手势解锁屏幕不陌生。 Android 的解锁屏幕由 \(3 \times 3\) 个点组成，手指在屏幕上画一条线，将其中一些点连接起来，即可构成一个解锁图案。如下面三个例子所示：

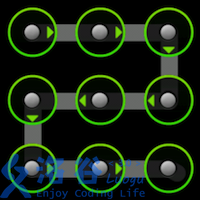
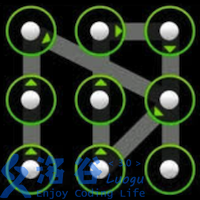
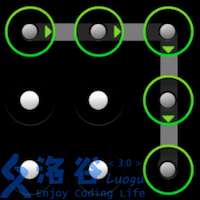
画线时还需要遵循一些规则：

1. 连接的点数不能少于 \(4\) 个。也就是说只连接两个点或者三个点会提示错误。
2. 两个点之间的联线不能弯曲。
3. 每个点只能“使用”一次，不可重复。这里的“使用”是指手指划过一个点，该点变绿。
4. 两个点之间的连线不能“跨过”另一个点，除非那个点之前已经被“使用”过。

对于最后一条规则，参见下图的解释。左边两幅图违反了该规则；而右边两幅图（分别为 $ 2 \rightarrow 4 \rightarrow 1 \rightarrow 3 \rightarrow 6$ 和 $ 6 \rightarrow 5 \rightarrow 4 \rightarrow 1 \rightarrow 9 \rightarrow 2$ ）则没有违反规则，因为在“跨过”点时，点已经被使用过了。

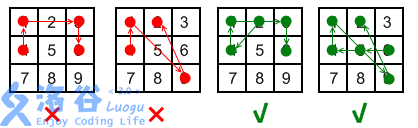
现在工程师希望改进解锁屏幕，增减点的数目，并移动点的位置，不再是一个九宫格形状，但保持上述画线规则不变。

请计算新的解锁屏幕上，一共有多少满足规则的画线方案。

对于 \(30\%\) 的数据， \(1 \le n \le 10\) 。
对于 \(100\%\) 的数据， \(-1000 \le x_i ,y_i \le 1000\) ， $ 1 \le n < 20$ 。各点坐标不相同。

题解

状压DP。

代码

#include<iostream>
#include<cmath>
using namespace std;
const int mod=1e8+7;
int n,x[30],y[30],bit[30],S[30][30];
int dp[1<<20][21],ans;
double dis(int i,int j) {return sqrt((x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j]));}
int main()
{
	cin>>n;bit[0]=1;
	for(int i=1;i<=n;i++) cin>>x[i]>>y[i];
	for(int i=1;i<=21;i++) bit[i]=1<<(i-1);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			for(int k=1;k<=n;k++)
				if(fabs(dis(i,j)-dis(i,k)-dis(j,k))<1e-8&&k!=i&&k!=j)
					S[i][j]|=bit[k];
	for(int i=1;i<=n;i++) dp[bit[i]][i]=1;
	for(int zt=0;zt<bit[n+1];zt++)
		for(int i=1;i<=n;i++)
			if(dp[zt][i])
				for(int j=1;j<=n;j++)
				{
					if(bit[j]&zt) continue;
					if((S[i][j]&zt)!=S[i][j]) continue;
					(dp[zt|bit[j]][j]+=dp[zt][i])%=mod;
				}
	for(int zt=0,res=0;zt<bit[n+1];res=0,zt++)
	{
		for(int i=1;i<=n;i++) if(zt&bit[i]) res++;
		if(res<=3) continue;
		for(int i=1;i<=n;i++) (ans+=dp[zt][i])%=mod;
	}
	cout<<ans<<endl;
}

D2T2 九连环

题意

九连环是一种源于中国的传统智力游戏。如图所示，九个圆环套在一把“剑”上，并且互相牵连。游戏的目标是把九个圆环从“剑”上卸下。

圆环的装卸需要遵守两个规则。

1. 第一个（最右边）环任何时候都可以装上或卸下。
2. 如果第 \(k\) 个环没有被卸下，且第 \(k\) 个环右边的所有环都被卸下，则第 \(k+1\) 个环（第 \(k\) 个环左边相邻的环）可以任意装上或卸下。

与魔方的千变万化不同，解九连环的最优策略是唯一的。为简单起见，我们以“四连环”为例，演示这一过程。这里用 1 表示环在“剑”上， 0 表示环已经卸下。

初始状态为 1111 ，每部的操作如下：

1. 1101 （根据规则 \(2\) ，卸下第 \(2\) 个环）
2. 1100 （根据规则 \(1\) ，卸下第 \(1\) 个环）
3. 0100 （根据规则 \(2\) ，卸下第 \(4\) 个环）
4. 0101 （根据规则 \(1\) ，装上第 \(1\) 个环）
5. 0111 （根据规则 \(2\) ，装上第 \(2\) 个环）
6. 0110 （根据规则 \(1\) ，卸下第 \(1\) 个环）
7. 0010 （根据规则 \(2\) ，卸下第 \(3\) 个环）
8. 0011 （根据规则 \(1\) ，装上第 \(1\) 个环）
9. 0001 （根据规则 \(2\) ，卸下第 \(2\) 个环）
10. 0000 （根据规则 \(1\) ，卸下第 \(1\) 个环）

由此可见，卸下“四连环”至少需要 \(10\) 步。随着环数增加，需要的步数也会随之增多。例如卸下九连环，就至少需要 \(341\) 步。
请你计算，有 \(n\) 个环的情况下，按照规则，全部卸下至少需要多少步。

对于 \(10\%\) 的数据， \(1 \le n \le 10\) 。
对于 \(30\%\) 的数据， \(1 \le n \le 30\) 。
对于 \(100\%\) 的数据， \(1 \le n \le 10^5 , 1 \le m \le 10\) 。

题解

通过这\(f[4]\)的演示，可以发现：\(f[4]=f[2]+1+f[2]+f[3]\)，所以得到递推：\(f[i]=2f[i-2]+f[i]+1\)

所以通过观察可得，\(f[2k+1]=\frac{4^{k+1}-1}{3},f[2k]=\frac{f[2k+1]-1}{2}\)

于是把\(4\)的1到16次方高精度预处理出来，然后直接上高精度乘法除法就好了。

不知道为什么要FFT

代码

#include<iostream>
#include<cstring>
using namespace std;
int m,n;
struct Bignum
{
	int a[100000],l;
	Bignum () {memset(a,0,sizeof(a));l=0;}
	void del()
		{
			a[1]--;
			for(int i=1;i<l;i++)
				if(a[i]<0) a[i]=9,a[i+1]--;
		}
	void div(int x)
		{
			for(int i=l,res=0;i>=1;i--)
				res+=a[i],a[i]=res/x,res%=x,res*=10;
			while(!a[l]) l--;
		}
	Bignum operator * (Bignum A)
		{
			Bignum C;C.l=A.l+l-1;
			for(int i=1;i<=l;i++)
				for(int j=1;j<=A.l;j++)
					C.a[i+j-1]+=a[i]*A.a[j];
			for(int i=1;i<C.l;i++) C.a[i+1]+=C.a[i]/10,C.a[i]%=10;
			while(C.a[C.l]>9) C.a[C.l+1]+=C.a[C.l]/10,C.a[C.l]%=10,C.l++;
			while(!C.a[C.l]) C.l--;
			return C;
		}
	void print() {for(int i=l;i>=1;i--) printf("%d",a[i]);puts("");}
}bs[17],Ans;
int main()
{
	bs[0].l=1;bs[0].a[1]=4;
	for(int i=1;i<=16;i++) bs[i]=bs[i-1]*bs[i-1];
	for(cin>>m;m;m--)
	{
		cin>>n;Ans.l=Ans.a[1]=1;
		int k=(n-(n&1))/2+1;
		for(int i=0;i<=16;i++)
			if(k&(1<<i)) Ans=Ans*bs[i];
		Ans.del(),Ans.div(3);
		if(!(n&1)) Ans.del(),Ans.div(2);
		Ans.print();
	}
	return 0;
}

D2T3 异或序列

题意

已知一个长度为 \(n\) 的整数数列 \(a_1,a_2,\dots,a_n\) ，给定查询参数 \(l\) 、 \(r\) ，问在 \(a_l,a_{l+1},\dots,a_r\) 区间内，有多少子序列满足异或和等于 \(k\) 。也就是说，对于所有的 $ x,y ( l \le x \le y \le r)$ ，满足 $ a_x \oplus a_{x+1} \oplus \dots \oplus a_y=k $ 的 \(x,y\) 有多少组。

对于 \(30\%\) 的数据， \(1 \le n,m \le 1000\) 。
对于 \(100\%\) 的数据， \(1 \le n,m \le 10^5 , 0 \le k,a_i \le 10^5 , 1 \le l_j \le r_j \le n\) 。

题解

处理好异或前缀和后，也就是区间\(l,r\)内每一对\(s[i]=x,s[j]=x\oplus k\)都会对答案产生1的贡献。

用桶然后莫队就好了。

代码

#include<iostream>
#include<algorithm>
#include<cmath>
#define ll long long
using namespace std;
const int N=5e5;
int n,m,k,a[N],s[N],bel[N],tong[N],blk;
ll Ans;
struct Que{int l,r,id;ll ans;}Q[N];
int cmp (const Que&A,const Que&B) {return bel[A.l]==bel[B.l]?A.r<B.r:bel[A.l]<bel[B.l];}
int cmp1(const Que&A,const Que&B) {return A.id<B.id;}
void Add(int p) {Ans+=tong[s[p]^k];tong[s[p]]++;}
void Del(int p) {Ans-=tong[s[p]^k];tong[s[p]]--;}
int main()
{
	cin>>n>>m>>k;
	for(int i=1;i<=n;i++) scanf("%d",&a[i]),s[i]=s[i-1]^a[i];
	for(int i=1;i<=m;i++) scanf("%d%d",&Q[i].l,&Q[i].r),Q[i].id=i,Q[i].l--;
	blk=sqrt(n);
	for(int i=0,nw=0;i<=n;bel[i]=nw,i++) if(i%blk==0) nw++;
	sort(Q+1,Q+m+1,cmp);
	for(int i=1,l=1,r=0;i<=m;i++)
	{
		while(r<Q[i].r) Add(++r);
		while(l>Q[i].l) Add(--l);
		while(r>Q[i].r) Del(r--);
		while(l<Q[i].l) Del(l++);
		Q[i].ans=Ans;
	}
	sort(Q+1,Q+m+1,cmp1);
	for(int i=1;i<=m;i++) printf("%lld\n",Q[i].ans);
	return 0;
}

后记

CQOI搞什么啊题目质量一点都不行啊。

5道模板真的令人无发可说。。

自测起来除了D1T3大概是50分外，其他都秒了。

但是考场不开O2的话高精度可能会被卡。

总之最多550也是十分危险的，因为如果Noip是发挥良好的话是520的队线，但是我Noip炸了啊！

愿HNOI不会这样。。