8. 最大堆

一、最大堆的定义

最大堆是一棵完全二叉树，而且每个结点的值都不小于其孩子结点的值。

 

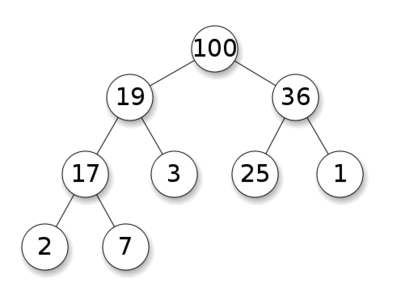
二、选择数组作为最大堆的内存表现形式

由于最大堆是一棵完全二叉树，所以我们使用数组的形式来存储最大堆的值，并从1号单元开始存储。

假设树的节点个数为n，以1为下标开始编号，直到n结束。对于下标为 i 的结点，其父结点的坐标为i / 2，左孩子结点的坐标为i * 2，右孩子结点的坐标为i*2 + 1。

例如，有数组heap[10] = {0, 100, 19, 36, 17, 3, 25, 1, 2, 7}，其对应的完全二叉树如下图所示。

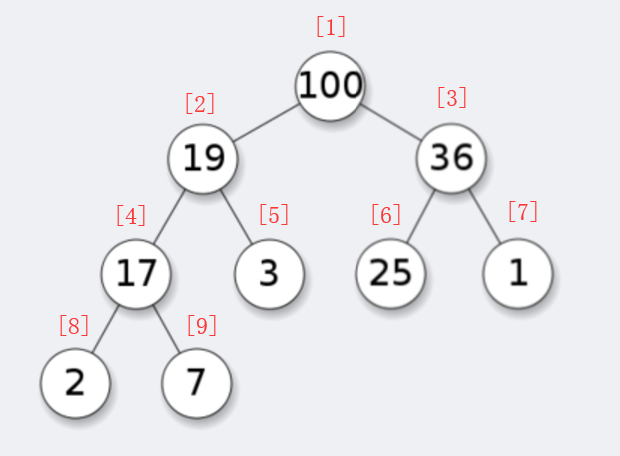
• heap[leftChild] = heap[father * 2]
• heap[rightChild] = heap[father * 2 + 1]
• heap[fathrt] = heap[leftChild / 2] = heap[rightChild / 2]

 

三、构造最大堆

构造堆的基本思想就是：首先将每个叶子结点视为一个堆，再将每个叶子结点与其父结点一起构造成一个包含更多节点的堆。

构造最大堆：首先需要找到最后一个结点的父结点，从这个结点开始构造最大堆，直到该结点前面的所有分支节点都处理完毕，这样最大堆就构造完毕了。

如下图所示，我们要将一个heap[11] = {0, 4, 1, 3, 2, 16, 9, 10, 14, 8, 7}的二叉完全树构造成最大堆。因为最后一个结点为7，其父结点为16，所以应从16这个结点开始构造最大堆；构造完毕之后，转移到下一个父结点2，直到所有父结点都构造完毕。

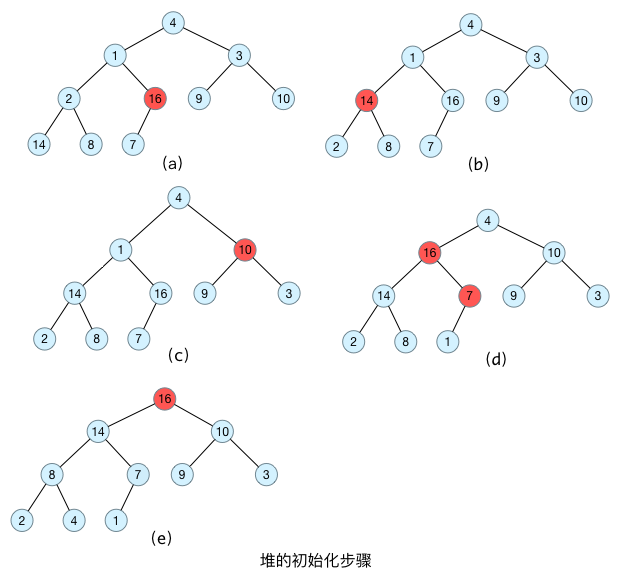
注：如上图(d)所示，当我们将结点1和结点16互换后，发现结点1又要和结点7互换。即结点1和结点16对调后，需要递归进行调整，请一定注意！

代码：

void create(MaxHeap &H)
{
	// 从最后一个结点的父结点开始构造最大堆 
	for(int i = H.heapSize / 2; i > 0; --i) {
		int temp = H.heap[i];			// 将父结点存放到temp中 
		// 本次for循环的以下过程皆是为了寻找父结点最终应存放的位置
		// 因为假设当前父结点与其子结点对调了，但它可能还要再与其下的新子结点对调
		
		// son一直记录当前父结点的孩子结点的坐标，所以它的值才一直在变  
		int son = i * 2;
		// 当前父结点递归下调过程				
		while(son <= H.heapSize) {
			// 右孩子结点的值更大 
			if(son < H.heapSize && H.heap[son] < H.heap[son+1])
				son++;
			// 当前父结点已是以其为根结点的最大堆的最大值 
			if(temp >= H.heap[son])
				break;
			// 需要与孩子结点对调，但此时尚不能退出循环，因为是递归下调 
			else {
				H.heap[son / 2] = H.heap[son];
				son = son * 2;
			}
		}
		H.heap[son/2] = temp;			// 找到父结点最终的位置，此时的son为父结点的最新孩子 
	}
} 

　　

四、插入

上浮：先在堆的最后添加一个结点，然后沿着堆上升，直到找到正确的插入位置。

过程：

1. 在下一个空闲位置创建一个空穴。

2. 如果元素X可以放在该空穴而并不破坏堆的序，那么插入完成；

3. 否则，我们把空穴的父结点上的元素移入该空穴中，继续该过程直到X能被放入空穴。

代码：

/* 插入值为x的结点 */
/*
 * 在堆的最后产生一个空穴，然后不断上移，直到找到能插入结点x的位置 
 * 空穴的最终位置就是结点x应插入的位置
 * 补：在空穴不断上移的过程中，要更换对应结点的值 
 */ 
bool insert(MaxHeap &H, int x)
{
	if(H.maxSize == H.heapSize)	
		return false;

	H.heapSize++;
	int xIndex = H.heapSize;		// 空穴的下标 
	while(xIndex != 1 && x > H.heap[xIndex / 2]) {
		H.heap[xIndex] = H.heap[xIndex / 2];	// 将那个比x小的根结点下沉到空穴 
		xIndex = xIndex / 2;					// 空穴上浮到新的位置（上浮一层） 
	} 
	H.heap[xIndex] = x;
	return true; 
}

 

五、删除最大元

下沉：将堆的最后的结点提到根结点，然后删除最大值，然后再把新的根节点放到合适的位置。

过程：

1. 删除最大元后，会在根结点处产生一个空穴。

2. 由于堆中少了一个元素，故堆中最后一个元素X必须移动到该堆的某个地方。

3. 将空穴的两个儿子中较小者移入空穴，重复该过程直到X可以被放入空穴中。

代码：

/* 删除根结点 */
bool deleteMax(MaxHeap &H)
{
	if(H.heapSize == 0)
		return false;
	// 将最后一个结点存到temp中 ，因为temp是要填入空穴的数，也即空穴的值就是temp 
	int temp = H.heap[H.heapSize];			
	H.heapSize--;
	// 空穴出现在堆的根结点处，即下标为1处 
	int newIndex = 1, son = newIndex * 2;		// son一直为空穴的孩子结点，随着空穴的下沉而改变
	// 当空穴没有到最后一个位置时 
	while(newIndex < H.heapSize) {
		// 右孩子结点的值更大 
		if(newIndex < H.heapSize && H.heap[son] <= H.heap[son+1]) 
			son++;
		// 孩子结点的值比空穴的值大，空穴下沉	
		if(H.heap[son] > temp) {
			H.heap[newIndex] = H.heap[son];
			newIndex = son;
			son = son * 2;	
		}
		// 得到空穴的最终位置 
		if(H.heap[son] <= temp)
			break;
	}
	H.heap[newIndex] = temp;
	return true;
}