DFS（1）——hdu1518Square

一、题目回顾

题目链接：Square

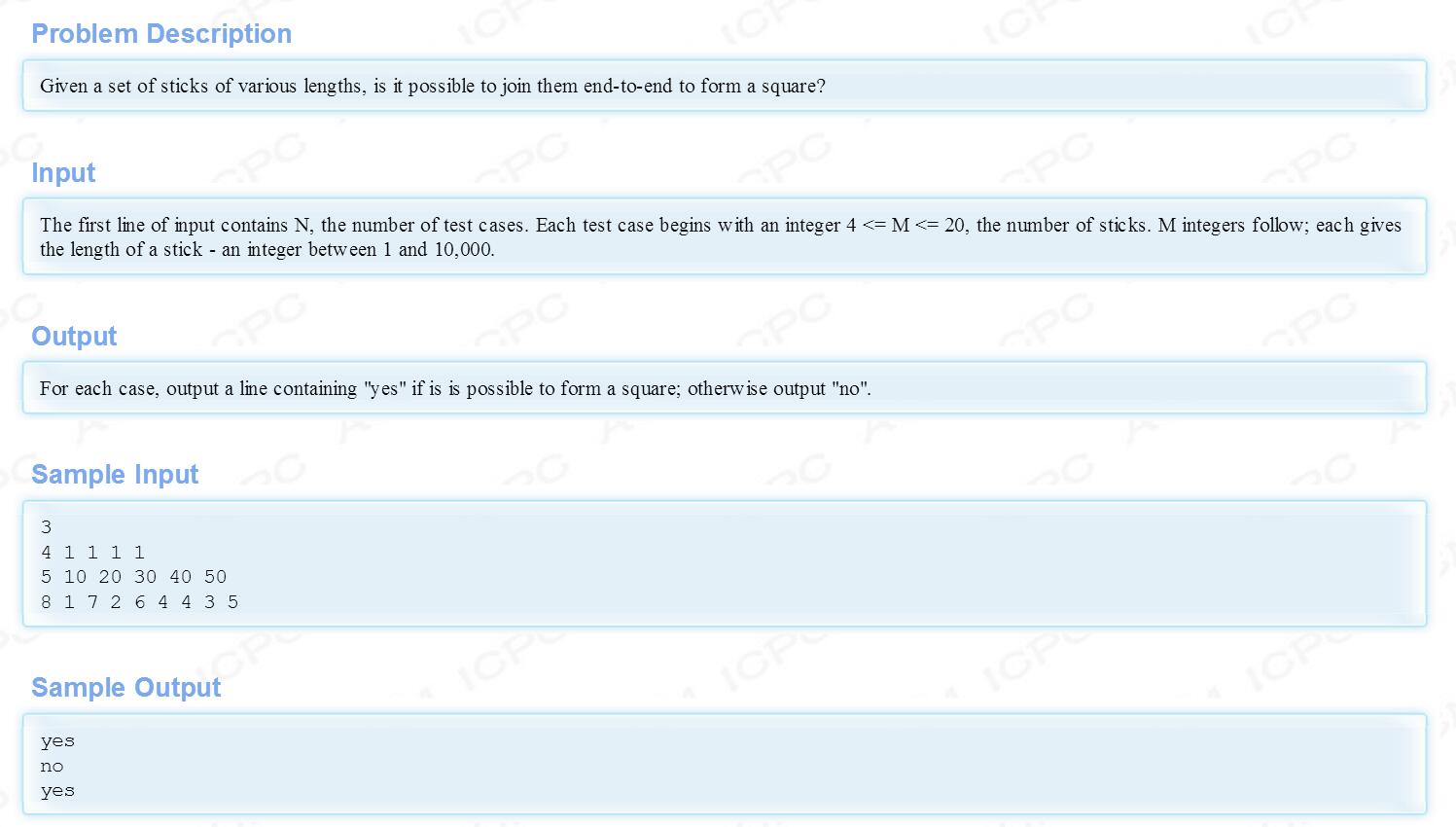
题意：给你M根木棒，请判断这些木棒能否组成正方形。

 

二、解题思路

• DFS+剪枝

【变量说明】

sum：木棒的总长度

ave：形成的正方形的边长

maxlen：最长木棒的长度

【剪枝】

1.  “num%4!=0”：表示木棒的总长度不是4的倍数，那么不能形成正方形
2. “maxlen>ave”：表示最长木棒的长度大于“边长”，也不可能形成正方形
3. 还有dfs语句内的剪枝，见下面分析。

【搜索过程】

dfs代码：

void dfs(int num,int len,int start)        //已凑完的边数，正在凑的这条边的长度，从序号为start的木棍开始找 
{
//语句块1 
    if(num==4){
        flag = 1;
        return;                            //有4条边时,即可返回 
    }
//语句块2 
    if(len==ave){
        dfs(num+1,0,0);
    }
//语句块3 
    for(int i=start;i<m;i++){              //遍历自start开始的边 
        if(!vis[i] && a[i]+len<=ave){      //如果这条边没访问过且加上这条边的长度小于边长 
            vis[i] = 1;                    //将这条边标记 
            dfs(num,a[i]+len,i+1);         //如此调用,则当len=ave时会调用dfs(num+1,0,0) 　　　　　　　　　　
            if(flag)    return;            //如果略去此句，会超时 
            vis[i] = 0;                       //此棒不可用 
        }
    }    
}

下面来具体解释一下dfs函数是怎么运作的。

【形式参数】

• num：已经凑完的边数
• len：正在凑的这条边的长度
• start：从第start根木棍开始找满足条件的木棍

【语句块1】

• “num==4”成立，即凑完4条边了，则令标记变量flag为1，并退出此轮调用；
• 何为“退出此轮调用”？简单来说，这个返回是返回到调用它的那个语句块内，而不是main函数中。

【语句块2】

• 当上级调用传入的实参与正方形的边长相等时，那么凑成的边数就加1，并调用dfs(num+1,0,0)；
• 能进入这个语句块，间接说明了凑完的边数小于4，那么调用dfs(num+1,0,0)就成立；
• “dfs(num+1,0,0)”，即正在凑成的边为0，从序号为0的棍子开始查找（这样对其他已用于形成边的棍子无影响，因为用于凑成其他的边数的棍子已经被标记）。

【语句块3】

• 能到达这一步，说明当前调用并不能满足“num==4”以及“len==sum/4”；
• “for(int i=start;i<m;i++)”，即从序号为start的棍子开始寻找，直到最后一根棍子；
• “if(!vis[i] && a[i]+len<=ave)”，即找到序号为i的棍子没被用于形成其他边并且它的长度+已经凑成长度<=边长；
• “vis[i]=1”，找到这个可行的棍子后，就说明这个棍子被用于形成边了（打上标记）；
• “dfs(num,len+a[i],i+1)”：首先谈“i+1”，你可能会问，为何是i+1而不是start或者是0呢？其实，这相当于剪枝，由本语句块内的if语句的判定条件式能确定第start根木棍到第i根木棍之前没有木棍能用于形成这条边，故无需再次判定（即令其为i+1）；
• “dfs(num,len+a[i],i+1)”：再谈len+a[i]，这个将正在凑的这条边的长度进行更新。由本语句块内的if语句的判定条件式能确定a[i]+len<=ave，试想，如果len+a[i]==ave，那么就会进入语句块2，然后调用dfs(num+1,0,0)，此时凑完的边数加1，即离成功越来越近，再往后或者进入语句块1(num==4)，或者进入语句块3；如果len+a[i]<ave，会再次进入语句块3，那么如果自第i+1根棍子开始至第m-1根棍子没有满足语句块3内if语句的判定条件的棍子，那么会结束此轮调用（这轮调用的发起者为第i根棍子），即表明第i根棍子不能加入这条正在形成的边内；
• “if(flag)  return;”，如果上面的dfs语句能够进入语句块1而使flag=1，就会返回主函数（节省时间），否则不返回主函数；
• “vis[i]=0”，这条棍子不能使这条边最终形成，故不选用此棍子，此棍子恢复自由。

【重点再理解】

• vis[i] = 1;  dfs(num,a[i]+len,i+1);  if(flag)    return;  vis[i] = 0;   

陈述法：第i根木棒满足未被选用且满足已凑成的长度+a[i]<=边长，那么我们就假设选用它（vis[i]=1），但实际上我们并不能确定它就一定是这条边的一部分，我们要检测在它之后加入的其他木棒能否形成正方形，于是我们dfs(num,a[i]+len,i+1)。这是一个调用函数，它的返回调用在语句块1中，显然，如果从语句块1中结束调用，会有flag=1，执行if(flag)语句，会成功return回到主函数，即整个DFS调用结束（因为num==4，正方形已形成），如果缺少if(flag)语句，会执行vis[i]=0，这会浪费大量时间。再回到dfs(num,a[i]+len,i+1)，如果选用的第i根木棒不能使后面加入的木棒形成正方形（即恒进不了语句块1），那么就有flag=0，于是不会返回到主函数，会执行vis[i]=0，然后继续执行for语句，寻找其他的木棒。

【深搜的理解】

由于过程中要确定某根木棒是否确定成功被接收，它就得提前预知加入这根木棒后其它的木棒能不能匹配成功，就叫要求在遍历某个木棒时，对其后的木棒进行递归搜索（深搜的特点）。若能匹配成功，则标记当前小木棒为用过，可以直接返回（试探成功）；若不能匹配，说明此棒目前不可用，将标记取消，待下一次搜索用。

 

三、代码

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
int n,m,sum,maxlen,flag;
int a[25];
bool vis[25];

void dfs(int num,int len,int x)        //已形成的边数，正在形成的边的长度，第几根木棒
{
    if(num==4){
        flag = 1;
        return;
    }    
    if(len==sum/4){
        dfs(num+1,0,1);
    }
    for(int i=x;i<=m;i++){
        if(!vis[i] && a[i]+len<=sum/4){
            vis[i] = 1;
            dfs(num,a[i]+len,i+1);        //剪枝：前面的棒棒已经访问过，他们并不能用于形成这条边
            if(flag==1)    return;            //省略会TLE 
            vis[i] = 0; 
        }
    }
} 

int main()
{
    scanf("%d",&n);
    while(n--){
        scanf("%d",&m);
        sum = 0;maxlen = 0;
        for(int i=1;i<=m;i++){
            scanf("%d",&a[i]);
            sum += a[i];
            if(a[i]>maxlen)    maxlen = a[i];
        }
        if(sum%4 || maxlen>sum/4){            //剪枝：根据题意判断 
            printf("no\n");
            continue;
        }
        flag = 0;
        memset(vis,0,sizeof(vis));
        dfs(0,0,1);
        if(flag==1)    printf("yes\n");
        else    printf("no\n");
    }
    return 0;
}