DFS实现模板

以如下图的无向图G4为例，进行图的深度优先搜索：

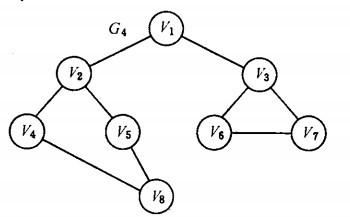
假设从顶点v₁出发进行搜索，在访问了顶点v₁之后，选择邻接点v₂。因为v₂未曾访问，则从v₂出发进行搜索。依次类推，接着从v₄ 、v₈ 、v₅出发进行搜索。在访问了v₅之后，由于v₅的邻接点都已被访问，则搜索回到v₈。由于同样的理由，搜索继续回到v₄，v₂直至v₁，此时由于v₁的另一个邻接点未被访问，则搜索又从v₁到v₃，再继续进行下去由此，得到的顶点访问序列为：

代码：

/*    图的DFS遍历    */
//邻接矩阵形式实现 
//顶点从1开始 
#include<iostream>
#include<cstdio>
using namespace std;
const int maxn = 105;        //最大顶点数 
typedef int VertexType;     //顶点类型
bool vis[maxn];  

struct Graph{               //邻接矩阵表示的图结构
    VertexType vex[maxn];   //存储顶点
    int arc[maxn][maxn];    //邻接矩阵
    int vexnum,arcnum;      //图的当前顶点数和弧数
};

void createGraph(Graph &g)  //构建无向图
{
    cout<<"请输入顶点数和边数：";
    cin>>g.vexnum>>g.arcnum;
     
    //构造顶点向量
    cout<<"请依次输入各顶点：\n";
    for(int i=1;i<=g.vexnum;i++){
        scanf("%d",&g.vex[i]);
    }
     
    //初始化邻接矩阵
    for(int i=1;i<=g.vexnum;i++){
        for(int j=1;j<=g.vexnum;j++){
            g.arc[i][j] = 0;
        }
    }
     
    //构造邻接矩阵
    VertexType u,v;     //分别是一条弧的弧尾(起点)和弧头(终点)
    printf("每一行输入一条弧依附的顶点（空格分开）：\n");
    for(int i=1;i<=g.arcnum;i++){
        cin>>u>>v;
        g.arc[u][v] = g.arc[v][u] = 1; 
    }  
}

//邻接矩阵的深度优先递归算法
void DFS(Graph g,int i)
{
    vis[i] = true;
    printf("%d\t",g.vex[i]);                //打印顶点 
    for(int j=1;j<=g.vexnum;j++){            //遍历每个顶点 
        if(g.arc[i][j]==1 && !vis[j]){        //如果顶点j是顶点i的未访问的邻接点 
            DFS(g,j);                        //深度优先搜索顶点j 
        }
    }
}

//邻接矩阵的深度遍历操作
void DFSTraverse(Graph g)
{
    for(int i=1;i<=g.vexnum;i++){
        vis[i] = false;                        //初始化所有顶点状态都是未访问过状态
    }
    for(int i=1;i<=g.vexnum;i++){
        if(!vis[i]){
            DFS(g,i);                        //对未访问的顶点调用DFS，若是连通图，只会执行一次
        }
    }
}

int main()
{
    Graph g;
    createGraph(g);
    DFSTraverse(g);
    return 0;
}