图的建立——图的两种存储结构

【前言】

图状结构是一种比树形结构更复杂的非线性结构。

在树状结构中，结点间具有分支层次关系，每一层的结点可以和下一层的多个结点相关，但只能和上一层中的一个结点相关。

而在图状结构中，任意两个结点之间都可能相关，即结点之间的邻接关系可以是任意的。

一、邻接矩阵

图和树一样，没有顺序映像的存储结构，但可以借助数组表示元素之间的关系。

邻接矩阵是用于描述图中顶点之间关系(即弧或边的权)的矩阵。

若图G中有n个顶点，则邻接矩阵是一个n×n的方阵，定义为：

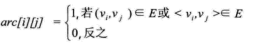
若图G是一个有n个顶点的带权图（即网），有n个顶点，则邻接矩阵可定义为：

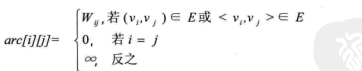
图的邻接矩阵存储方式是用两个数组来表示图：

• 一个一维数组vex：存储图中顶点信息；
• 一个二维数组arc：存储图中顶点之间关系（即弧或边）的信息。

//邻接矩阵表示法 
//有向网 
#include<iostream>
#include<cstdio>
using namespace std;
#define INFINITY 32767		//最大值，假定为无穷大 
const int maxn = 10;

typedef int VertexType;		//顶点类型
typedef int VRType;			//顶点关系类型，对于无权图，用0或1表示相邻否；对于带权图，则为相应权值
 
struct Graph{				//邻接矩阵表示的图结构 
	VertexType vex[maxn];	//存储顶点 
	int arc[maxn][maxn];	//邻接矩阵 
	int vexnum,arcnum;		//图的当前顶点数和弧数 
};

int locateVex(Graph g,VertexType v)	//若图中存在v，则返回v在图中的位置信息 
{
	for(int i=0;i<g.vexnum;i++){
		if(v == g.vex[i]){
			return i;
		}
	}
	return -1;				//图中无该顶点 
}

void createGraph(Graph &g)  //构建有向网g 
{
	cout<<"请输入顶点数和边数：";
	cin>>g.vexnum>>g.arcnum;
	
	//构造顶点向量 
	cout<<"请依次输入各顶点：\n"; 
	for(int i=0;i<g.vexnum;i++){
		scanf("%d",&g.vex[i]);
	}
	
	//初始化邻接矩阵 
	for(int i=0;i<g.vexnum;i++){
		for(int j=0;j<g.vexnum;j++){
			g.arc[i][j] = INFINITY;
		}
	}
	
	//构造邻接矩阵 
	VertexType u,v;		//分别是一条弧的弧尾(起点)和弧头(终点) 
	VRType w;			//对于无权图，用0或1表示相邻否；对于带权图，则为相应权值
	printf("每一行输入一条弧依附的顶点（先弧尾，再弧头）和权值（如:u v w）：\n");
	for(int i=0;i<g.arcnum;i++){
		cin>>u>>v>>w;
		int v1_index = locateVex(g,u);
		int v2_index = locateVex(g,v);
		g.arc[v1_index][v2_index] = w;  
	}	
}

void print(Graph g)
{
	cout<<"打印有向网g的邻接矩阵：\n";
	for(int i=0;i<g.vexnum;i++){
		for(int j=0;j<g.vexnum;j++){
			if(g.arc[i][j] != INFINITY)
				printf("%5d",g.arc[i][j]);
			else{
				printf("   -1");	//表示两点之间不直接相连 
			}
		}
		printf("\n");
	}
	printf("\n");
}

int main()
{
	Graph g;
	createGraph(g);
	print(g);
	return 0;
}

若现在有一个有向网及它的邻接矩阵如下图所示：

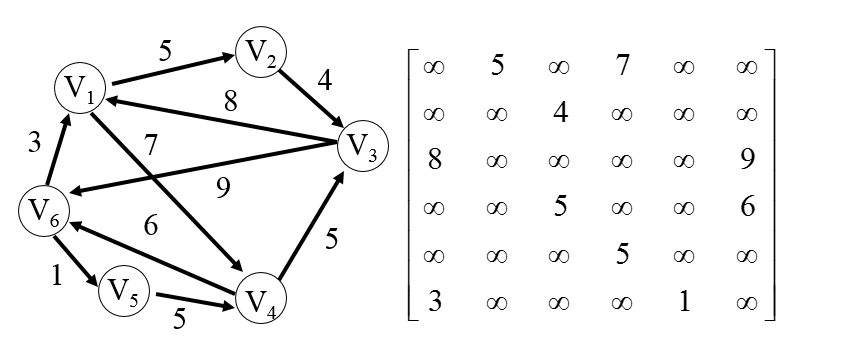
那么，执行上面程序，我们得到：

 

二、邻接表

对于图来说，邻接矩阵是不错的一种图存储结构，但是我们也发现，对于边数相对顶点较少的图，这种结构是存在对存储空间的极大浪费的。

因此我们考虑另外一种存储结构方式：邻接表，即数组与链表相结合的存储方法。

图的邻接表存储方式是用一个数组和一个单链表来表示图：

• 图中顶点用一个一维数组存储，另外，对于顶点数组中，每个数据元素还需要存储指向第一个邻接点的指针，以便于查找该顶点的边信息。
• 图中每个顶点v_i的所有邻接点构成一个线性表，由于邻接点的个数不定，所以，用单链表存储。无向图称为顶点v_i的边表，有向图则称为顶点v_i作为弧尾的出边表。

例如，下图就是一个无向图的邻接表的结构。

 

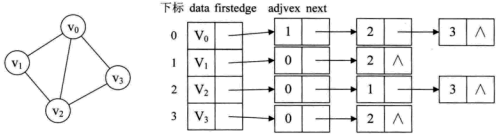
从图中可以看出，顶点表的各个结点由data和firstedge两个域表示，data是数据域，存储顶点的信息，firstedge是指针域，指向边表的第一个结点（即此顶点的第一个邻接点）。边表结点由adjvex和next两个域组成。adjvex是邻接点域，存储某顶点的邻接点在顶点表中的下标，next则存储指向边表中下一个结点的指针。

若是有向图，邻接表的结构是类似的，如下图。

以顶点作为弧尾来存储边表容易得到每个顶点的出度，而以顶点为弧头的表容易得到顶点的入度，即逆邻接表。

对于带权值的网图，可以在边表结点定义中再增加一个weight的数据域，存储权值信息即可。如下图所示。

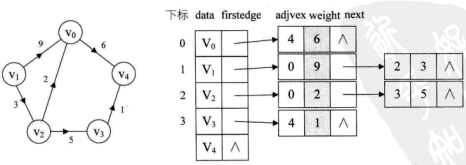
以无向网为例，可有如下邻接表：

类似树的孩子链表。即对图中的每个顶点v_i建立一个单链表，表中结点表示依附于该顶点v_i的边或弧。

顶点结点（弧链表表头结点）， 弧结点。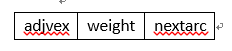

#include<iostream>
#include<cstdio>
#include<cstdlib>
using namespace std;
#define INFINITY 32767		//最大值，假定为无穷大 
const int maxn = 10;		//最大顶点数

typedef int VertexType;		//顶点类型
typedef int VRType;			//边上的权值类型，对于带权图或网，则为相应权值 

typedef struct ArcNode{			//边表结点，亦指弧节点信息 
	int adjvex;					//邻接点域,存储该顶点对应的下标，亦指该弧所指向的顶点的在图中位置 
	VRType w;					//用于存储权值,对于非网图可以不需要
	struct ArcNode *nextarc;	//链域,指向下一个邻接点;指向下一条弧的指针 
}ArcNode; 
typedef struct VNode{			//顶点表结点，亦指顶点节点信息 
	VertexType data;			//顶点域,存储顶点信息
	ArcNode *firstarc;			//边表头指针，指向第一条依附该顶点的弧的指针 
}VNode;
//VNode AdjVexList[maxn]; 
struct Graph{			//邻接表表示的图
	VNode vex[maxn];		//顶点向量 
	int vexnum,arcnum;	//图中当前顶点数和边数
};
 
int locateVex(Graph g,VertexType v)	//若图中存在v，则返回v在图中的位置信息 
{
	for(int i=0;i<g.vexnum;i++){
		if(v == g.vex[i].data){
			return i;
		}
	}
	return -1;				//图中无该顶点 
}

void createGraph(Graph &g) 						//构建无向网g 
{
	cout<<"请输入顶点数和边数(空格分隔）：";
	cin>>g.vexnum>>g.arcnum;
	
	//构造顶点向量,并初始化
	cout<<"请依次输入各顶点：\n"; 
	for(int i=0;i<g.vexnum;i++){
		scanf("%d",&g.vex[i].data);
		g.vex[i].firstarc = NULL;				//将边表置为空表，初始化为空指针 
	}
	
	//构造邻接表，亦指建立边表 
	VertexType u,v;			//分别是一条弧的弧尾和弧头（起点和终点）
	VRType w;				//对于无权图或网，用0或1表示相邻否；对于带权图或网，则为相应权值
	printf("每一行输入一条弧依附的顶点（先弧尾，再弧头）和权值（如:u v w）：\n");
	for(int i=0;i<g.arcnum;i++){
		cin>>u>>v>>w;
		int v1_index = locateVex(g,u);	//弧起点
		int v2_index = locateVex(g,v);	//弧终点
		
		//采用“头插法”在各个顶点的弧链头部插入弧结点 
		ArcNode *p1 = (ArcNode *)malloc(sizeof(ArcNode));	//构造一个弧结点，作为弧vivj的弧头（终点）
		p1->adjvex = v2_index;		//邻接序号为v2_index
		p1->w = w;
		/* 将p1的指针指向当前顶点上指向的结点 */
		p1->nextarc = g.vex[v1_index].firstarc;
		g.vex[v1_index].firstarc = p1; 						//将当前顶点的指针指向p1
		ArcNode *p2 = (ArcNode *)malloc(sizeof(ArcNode));	//构造一个弧结点，作为弧vivj的弧尾（起点） 
		p2->adjvex = v1_index;
		p2->w = w;
		p2->nextarc = g.vex[v2_index].firstarc;
		g.vex[v2_index].firstarc = p2;
		
	}	
}

//打印邻接表 
void print(Graph g)
{
	cout<<"\n";
	for(int i=0;i<g.vexnum;i++){
		printf("依赖顶点%d的弧为：",g.vex[i].data);
		ArcNode *p = g.vex[i].firstarc;
		while(p){
			printf("%d---%d(weight:%d) ",g.vex[i].data,g.vex[p->adjvex].data,p->w);
			p = p->nextarc;
		}
		printf("\n");
	}
	printf("\n");
}

int main()
{
	Graph g;
	createGraph(g);
	print(g);
	return 0;
	
}

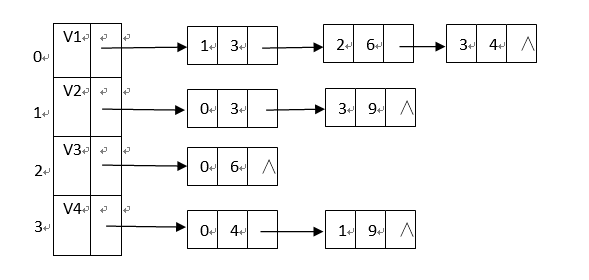
若现有一个无向网及其邻接表如下图所示，

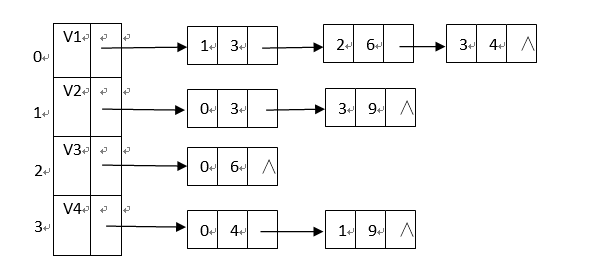
执行上面程序，有：

 

三、其他

十字链表点击

邻接多重表及十字链表点击