最短路径——Bellman-Ford算法
一、相关定义
最短路径:求源点到某特定点的最短距离
特点:Bellman-Ford算法主要是针对有负权值的图,来判断该图中是否有负权回路或者存在最短路径的点
局限性:算法效率不高,不如SPFA算法
时间复杂度:O(mn)
【具体与dijkstra算法的比较】
Bellman-Ford算法为何需要循环n-1次来求解最短路径?Dijkstra从源点开始,更新dis[],找到最小值,再更新dis[]……每次循环都可以确定一个点的最短路。Bellman-Ford算法同样也是这样,它的每次循环也可以确定一个点的最短路,只不过代价很大,因为 Bellman-Ford每次循环都是操作所有边。既然代价这么大,相比Dijkstra 算法,Bellman-Ford算法还有啥用?因为后者可以检测负权回路啊。Bellman-Ford 算法的时间复杂度为 O(nm),其中 n 为顶点数,m 为边数。
【负权回路】
开始不懂,看了下面的图和我的算法描述后就懂了:
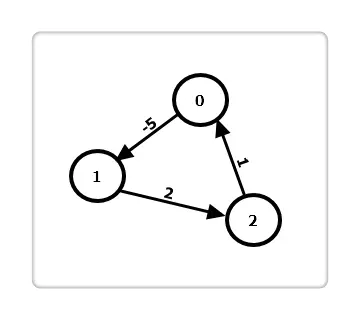
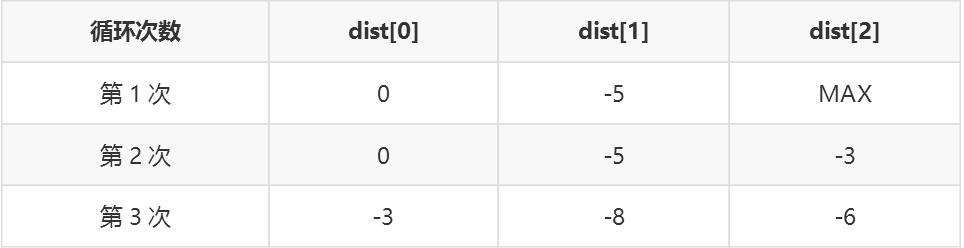
在循环n-1次的基础上再次遍历各边,对于所有边,只要存在一条边e(u, v)使得 dis[u] + w(u,v) < dis[v],则该图存在负权回路。
【松弛操作】

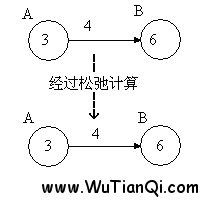
如左图所示,松弛计算之前,点B的值是8,但是点A的值加上边上的权重2,得到5,比点B的值(8)小,所以,点B的值减小为5。这个过程的意义是,找到了一条通向B点更短的路线,且该路线是先经过点A,然后通过权重为2的边,到达点B。
当然,如果出现右边这种情况,则不会修改点B的值,因为3+4>6。
二、算法描述
关键词:初始化 松弛操作
主要变量如下:
int n 表示有n个点,从1~n标号
int s,t s为源点,t为终点
int dis[N] dis[i]表示源点s到点i的最短路径
int pre[N] 记录路径,pre[i]表示i的前驱结点
bool vis[N] vis[i]=true表示点i被标记
【初始化】
dis数组全部赋值为INF,pre数组全部赋值为-1(表示还不知道前驱),
dis[s] = 0 表示源点不要求最短路径(或者最短路径就是0)。
【松弛操作】
对于每一条边e(u, v),如果dis[u] + w(u, v) < dis[v],则另dis[v] = dis[u]+w(u, v)。w(u, v)为边e(u,v)的权值
注:上述循环执行至多n-1次。若上述操作没有对Distant进行更新,说明最短路径已经查找完毕或者部分点不可达,跳出循环;否则执行下次循环。
【检测负权回路】
为了检测图中是否存在负环路,即权值之和小于0的环路。
检测的方法很简单,只需在求解最短路径的 n-1 次循环基础上,再进行第 n 次循环:对于每一条边e(u, v),如果存在边使得dis[u] + w(u, v) < dis[v],则图中存在负环路,即是说改图无法求出单源最短路径。否则数组Distant[n]中记录的就是源点s到各顶点的最短路径长度。
【小结】
Bellman-Ford算法可以大致分为三个部分:
- 初始化所有点。每一个点保存一个值,表示从原点到达这个点的距离,将原点的值设为0,其它的点的值设为无穷大(表示不可达)。
- 进行循环,循环下标为从1到n-1(n等于图中点的个数)。在循环内部,遍历所有的边,进行松弛计算。
- 遍历途中所有的边(edge(u,v)),判断是否存在这样情况: d(v) > d (u) + w(u,v),若存在,则返回false,表示图中存在从源点可达的权为负的回路。
之所以需要第三步的原因,是因为,如果存在从源点可达的权为负的回路,则将因为无法收敛而导致不能求出最短路径。
三、代码实现
#include<iostream>
#include<stack>
using namespace std;
#define MAX 10000 //假设权值最大不超过10000
struct Edge
{
int u;
int v;
int w;
};
Edge edge[10000]; //记录所有边
int dist[100]; //源点到顶点i的最短距离
int path[100]; //记录最短路的路径
int vertex_num; //顶点数
int edge_num; //边数
int source; //源点
bool BellmanFord()
{
//初始化
for (int i = 0; i < vertex_num; i++)
dist[i] = (i == source) ? 0 : MAX;
//n-1次循环求最短路径
for (int i = 1; i <= vertex_num - 1; i++)
{
for (int j = 0; j < edge_num; j++)
{
if (dist[edge[j].v] > dist[edge[j].u] + edge[j].w)
{
dist[edge[j].v] = dist[edge[j].u] + edge[j].w;
path[edge[j].v] = edge[j].u;
}
}
}
bool flag = true; //标记是否有负权回路
//第n次循环判断负权回路
for (int i = 0; i < edge_num; i++)
{
if (dist[edge[i].v] > dist[edge[i].u] + edge[i].w)
{
flag = false;
break;
}
}
return flag;
}
void Print()
{
for (int i = 0; i < vertex_num; i++)
{
if (i != source)
{
int p = i;
stack<int> s;
cout << "顶点 " << source << " 到顶点 " << p << " 的最短路径是: ";
while (source != p) //路径顺序是逆向的,所以先保存到栈
{
s.push(p);
p = path[p];
}
cout << source;
while (!s.empty()) //依次从栈中取出的才是正序路径
{
cout << "--" << s.top();
s.pop();
}
cout << " 最短路径长度是:" << dist[i] << endl;
}
}
}
int main()
{
cout << "请输入图的顶点数,边数,源点:";
cin >> vertex_num >> edge_num >> source;
cout << "请输入" << edge_num << "条边的信息:\n";
for (int i = 0; i < edge_num; i++)
cin >> edge[i].u >> edge[i].v >> edge[i].w;
if (BellmanFord())
Print();
else
cout << "Sorry,it have negative circle!\n";
return 0;
}
运行截图:







