大数据算法
大数据算法 #
参考：http://blog.csdn.net/hguisu/article/details/7856239
http://www.cnblogs.com/allensun/archive/2011/02/16/1956532.html
程序员代码面试指南-第六章
一、基本概念
所谓海量，就是数据量很大，可能是TB级别甚至是PB级别，导致无法一次性载入内存或者无法在较短时间内处理完成。面对海量数据，我们想到的最简单方法即是分治法，即分开处理，大而化小，小而治之。我们也可以想到集群分布式处理。
二、常用数据结构和算法
2.1 Bloom Filter
即布隆过滤器，它可以用于检索一个元素是否在一个集合中。在垃圾邮件的黑白名单过滤、爬虫(Crawler)的网址判重等中经常被用到。
Bloom Filter（BF）是一种空间效率很高的随机数据结构，它利用位数组很简洁地表示一个集合，并能判断一个元素是否属于这个集合。它是一个判断元素是否存在集合的快速的概率算法。Bloom Filter有可能会出现错误判断，但不会漏掉判断。也就是Bloom Filter判断元素不在集合，那肯定不在。如果判断元素存在集合中，有一定的概率判断错误。即：宁可错杀三千，绝不放过一个。因此，Bloom Filter不适合那些“零错误”的应用场合。而在能容忍低错误率的应用场合下，Bloom Filter相比其他常见的算法（如hash，折半查找），极大的节省了空间。
它的优点是空间效率和查询时间都优于一般的算法，缺点是有一定的误识别率和删除困难。
add和query的时间复杂度都为O(k)，与集合中元素的多少无关，这是其他数据结构都不能完成的。
Bloom-Filter算法的核心思想就是利用多个独立的Hash函数来解决“冲突”。Hash函数将一个元素（比如URL）映射到二进制位数组（位图数组）中的某一位，如果该位已经被置为1，只能说明该元素可能已经存在。因为Hash存在一个冲突（碰撞）的问题，即不同URL的Hash值有可能相同。为了减少冲突，我们可以多引入几个独立的hash函数，如果通过其中的一个Hash值我们得出某元素不在集合中，那么该元素肯定不在集合中。只有在所有的Hash函数告诉我们该元素在集合中时，才能在很大概率上认为该元素存在于集合中。
原理要点：一是m位的bit数组， 二是k个独立均匀分布的hash函数，三是误判概率p。
- m bits的bit数组：使用一个m比特的数组来保存信息，每一个bit位都初始化为0
- k个独立均匀分布的hash函数：为了添加一个元素，用k个hash函数将它hash得到bloom filter中k个bit位，将这k个bit位置1(超过m的取余%m)。
- 误判概率p：为了查询一个元素，即判断它是否在集合中，用k个hash函数将它hash得到k个bit位。若这k bits全为1，则此元素以概率(1-p)在集合中；若其中任一位不为1，则此元素必不在集合中（因为如果在，则在添加时已经把对应的k个bits位置为1）。
不允许移除元素，因为那样的话会把相应的k个bits位全置为0，而其中很有可能有其他元素对应的位。因此remove会引起误报，这是绝对不被允许的。而删除元素其实可以通过引入白名单解决。
当k很大时，设计k个独立的hash function是不现实并且困难的。对于一个输出范围很大的hash function（例如MD5产生的128 bits数），如果不同bit位的相关性很小，则可把此输出分割为k份。或者可将k个不同的初始值（例如0,1,2, … ,k-1）结合元素，赋值给一个hash 函数从而产生k个不同的数。
当add的元素过多时，即n/m过大时（n是元素数，m是bloom filter的bits数），会导致false positive(误判)过高，此时就需要重新组建filter，但这种情况相对少见。
若元素总数为n，误判率为p，则：
布隆过滤器的大小：
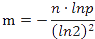
hash函数的个数：
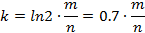
误判率p与m和n的关系：
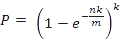
举个例子，我们假设错误率为p=0.01，则此时m大概是n的13倍，k大概是8个。
这里m与n的单位不同，m是bit为单位，而n则是以元素个数为单位(准确的说是不同元素的个数)。通常单个元素的长度都是有很多bit的，所以使用bloom filter内存上通常都是节省的。
误判概率的证明和计算
假设布隆过滤器中的hash function满足独立均匀分布地的假设：每个元素都等概率地hash到m个bit中的任何一个，与其它元素被hash到哪个bit无关。那么对某一个bit位来说，一个输入对象在被k个hash function散列后，这个位置依然为0的概率为：
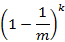
经过n个输入对象后，这个位置依然未被置1的概率为：
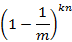
该位置被置1的概率：
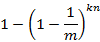
那么在检查阶段，若对应某个待query元素的k bits全部置位为1，则可判定其在集合中。因此将某元素误判的概率为：
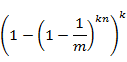
由于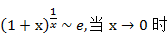
，并且
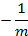当m很大时趋近于0，所以：
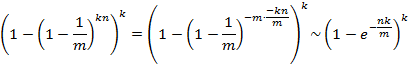
现在计算对于给定的m和n，k为何值时可以使得误判率最低。设误判率为k的函数为：
设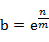
， 则简化为
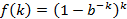，两边取对数：
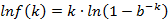
, 两边对k求导：
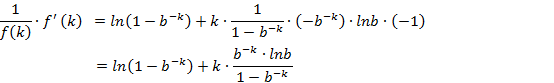
下面求最值：
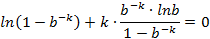
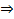
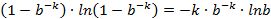
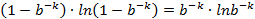
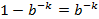
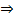
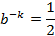
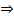
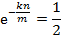
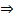
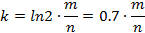
将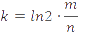
代入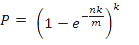
由\(a^{log_a^N}=N\),并两边取对数得到：
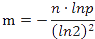
Bloom-Filter的应用
1、 key-value 加快查询
一般key-value存储系统的values存在硬盘，查询就是件费时的事。将Storage的数据都插入Filter，在Filter中查询都不存在时，那就不需要去Storage查询了。当False Position出现时，只是会导致一次多余的Storage查询。
由于Bloom-Filter所用的空间非常小，所有BF可以常驻内存。这样子的话，对于大部分不存在的元素，我们只需要访问内存中的Bloom-Filter就可以判断出来了，只有一小部分，我们需要访问在硬盘上的key-value数据库，从而大大地提高了效率。
2、垃圾邮件地址过滤
像网易，QQ这样的公众电子邮件（email）提供商，总是需要过滤来自发送垃圾邮件的人（spamer）的垃圾邮件。
一个办法就是记录下那些发垃圾邮件的 email地址。由于那些发送者不停地在注册新的地址，全世界少说也有几十亿个发垃圾邮件的地址，将他们都存起来则需要大量的网络服务器。
如果用哈希表，每存储一亿个 email地址，就需要 1.6GB的内存（用哈希表实现的具体办法是将每一个 email地址对应成一个八字节的信息指纹，然后将这些信息指纹存入哈希表，由于哈希表的存储效率一般只有 50%，因此一个 email地址需要占用十六个字节。一亿个地址大约要 1.6GB，即十六亿字节的内存）。因此存贮几十亿个邮件地址可能需要上百 GB的内存。
而Bloom Filter只需要哈希表 1/8到 1/4 的大小就能解决同样的问题。
BloomFilter决不会漏掉任何一个在黑名单中的可疑地址。而至于误判问题，常见的补救办法是在建立一个小的白名单，存储那些可能被误判的邮件地址。
2.2 Hash
Hash，一般翻译做“散列”，也有直接音译为“哈希”的，就是把一个对象的关键字，通过散列算法，映射到一个固定长度的数组中。当我们想要找到对应的对象时，只需要根据它的关键字在散列表中查找（再计算一次散列值）。这种转换是一种压缩映射，也就是，散列值的空间通常远小于输入的空间，不同的输入可能会散列成相同的输出，而不可能从散列值来唯一的确定输入值。输入叫做关键字，输出叫做散列值或者哈希地址（仅仅是在散列表中的地址）。但通常需要总数据量可以放入内存。
散列表是具有固定大小的数组，其中，表长(即数组的大小)应该为质数。
冲突：两个不同的输入计算出了相同的散列值。
散列函数一般应具备以下几个特点：
运算简单；函数的值域必须在散列表内；尽可能减少冲突；不同输入获得的散列值尽量均匀分散。
常用的散列函数：
- 直接定址法： 是以数据元素关键字k本身或它的线性函数作为它的哈希地址，即：hash（k）=k 或 hash（k）=a*k+b ； (其中a,b为常数)。此法仅适合于：地址集合的大小 = = 关键字集合的大小，比如以年龄为key，以年龄对应的人数为value
- 数字分析法：假设关键字集合中的每个关键字都是由 s 位数字组成 (u1, u2, …, us)，分析关键字集中的全体，并从中提取分布均匀的若干位或它们的组合作为地址。它只适合于所有关键字值已知的情况。
- 折叠法： 将关键字分割成若干部分，然后取它们的叠加和，留下t位作为哈希地址。适用于关键字位数较多，而且关键字中每一位上数字分布大致均匀的情况。
- 平方取中法： 这是一种常用的哈希函数构造方法。这个方法是先取关键字的平方，然后根据可使用空间的大小，选取平方数是中间几位为哈希地址。
- 减去法：数据的键值减去一个特定的数值以求得数据存储的位置。
- 除留余数法：这是一种常用的哈希函数构造方法。假设哈希表长为m，p为小于等于m的最大素数，则哈希函数为hash（k）=k % p ，其中%为模p取余运算。
Hash处理冲突方法：
- 开放定址法：这种方法也称探测散列法，其基本思想是：当关键字key的哈希地址p=hash（key）出现冲突时，以p为基础，产生另一个哈希地址p1，如果p1仍然冲突，再以p1为基础，产生另一个哈希地址p2，…，直到找出一个不冲突的哈希地址pi ，将相应元素存入其中。这种方法有一个通用的再散列函数形式：
Hi=(hash(key)+f(i))% m i=1，2，…，n
其中hash（key）为关键字key的直接散列地址，m 为表长，f(i)称为增量序列，表示每次再探测试时的地址增量。
这种方法如何查找元素x：
比如我们采用线性探测法，地址增量f(i)=2。其实就是按照计算hash位置的方法进行查找。首先计算hash(x)，如果这里有元素且不为x，则尝试hash(x)+2；如果这里有元素且不为x，则尝试hash(x)+2+2，一直到查找到的位置为null或者等于元素x。
-
再散列法：首先构造长度为length1的散列表table1，然后利用hash1(key)计算需要插入的元素的散列值。当散列表快要被插满时（比如达到了一定的装填因子，或者当插入失败时），再构造一个长度为length2=1+2*length1（实际不一定是2倍+1）的散列表table2，并将table1的元素按照hash2(key)散列到新表中，持续这样的过程...。
-
链地址法:基本思想是散列地址i保存一个单链表的头指针，所有散列值为i的元素都保存在i对应的单链表中，因而查找、插入和删除主要在单链表中进行。链地址法适用于经常进行插入和删除或者冲突比较严重的情况。例如，已知一组关键字（32，40，36，53，16，46，71，27，42，24，49，64），哈希表长度为13，哈希函数为：H（key）= key % 13，则用链地址法处理冲突的结果如图：
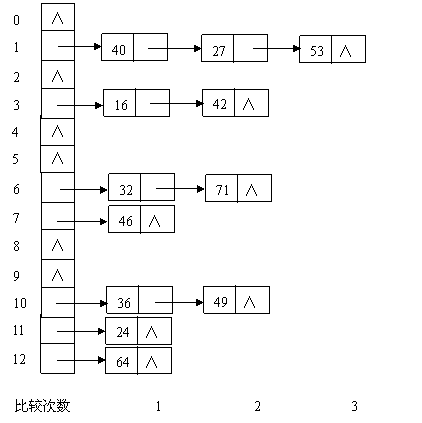
本例的平均查找长度 ASL=(17+24+3*1)=1.5 -
建立公共溢出区:将哈希表分为基本表和溢出表两部分，凡是和基本表发生冲突的元素，一律填入溢出表
Hash的应用
1、哈希对于检测数据对象（例如消息）中的修改很有用。好的哈希算法使得构造两个相互独立且具有相同哈希的输入不能通过计算方法实现。典型的哈希算法包括MD5 和 SHA-1。
2、海量日志数据分析，比如提取出某日访问百度次数最多的那个IP。
2.3 Bit-Map（位图）
Bit-map法的基本原理是：使用位数组来表示某些元素是否存在，每一个bit位可以标记一个元素对应的Value。
假设我们要对0-7内的5个元素(4,7,2,5,3)排序（这里假设这些元素没有重复）。那么我们就可以采用Bit-map的方法来达到排序的目的。要表示8个数，我们就只需要8个bit（1Bytes），首先我们开辟1Byte的空间，将这些空间的所有bit位都置为0，如下图：
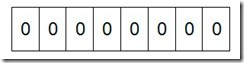
然后遍历这5个元素，首先第一个元素是4，那么就把4对应的位置为1,因为是从零开始的，所以要把第五位置为一（如下图）：
然后再处理第二个元素7，将第八位置为1,，接着再处理第三个元素，一直到最后处理完所有的元素，将相应的位置为1，这时候的内存的bit位的状态如下：
然后我们遍历一遍bit区域，将值为1的位的编号输出（2，3，4，5，7），这样就达到了排序的目的。
对于排序，优点是：运算效率高，不需进行比较和移位，时间复杂度是O(n)；占用内存少，比如N=10000000；只需占用内存为N/8=1250000Byte=1.25M。
缺点：数据最好是惆集数据(不然空间浪费很大)；数据不可重复(会将重复的数据覆盖掉)
位图的应用
1、判断集合中是否存在重复：
比如：
若集合大小为N，首先扫描一遍集合，找到集合中的最大元素max，然后创建一个长度为max+1的bit数组。接着再次扫描原集合，每遇到一个元素，就将新数组中下标为元素值的位置为1，比如，如果遇到元素5，则将新数组的第6个元素置为1，如此下去，当下次再遇到元素5想置位时，发现新数组的第6个元素已经被置为1了，则这个元素一定重复了。该算法的最坏运算次数2N，但如果能够事先知道集合的最大元素值，则运算次数N。
再比如：已知某个文件内包含一些电话号码，每个号码为8位数字，统计不同号码的个数。
8位最多99 999 999，大概需要99m个bit，大概10几m字节的内存即可。 （可以理解为从0-99 999 999的数字，每个数字对应一个bit位，所以只需要99M个bit=12MB多，这样，就用了小小的12M多左右的内存表示了所有的8位数的电话）
2、判断集合中某个元素是否存在:
比如：给你一个文件，里面包含40亿个非负整数，写一个算法找出该文件中不包含的一个整数， 假设你有1GB内存可用。如果你只有10MB的内存呢？
32位无符号整数的范围是0~4294967295(即2 x 2147483647+1)，因此可以申请一个长度为4294967295的bit数组bitArr，bitArr的每个位置只可以表示0或者1。8个bit为1B，所以长度为4294967295的数组占用内存：40*10^8bit=0.5GB=500MB。
然后遍历这40亿个无符号数，例如，遇到7000，就把bitArr[7000]置为1。遍历数字完成后，遍历bitArr，哪个位置的值为0，哪个数就不在这40亿个数内。
现在我们来看如果内存要求是10MB呢？
我们可以将所有04294967295的数据平均分成64个区间，每个区间保存67108864个数，比如：第0区间[067108863]，第1区间[67108864134217727]，第i区间为[67108864*i67108864(i+1)-1]...,实际上我们并不保存这些数，而是给每一个区间设置一个计数器。这样每读入一个数，我们就在它所在的区间对应的计数器加1。处理结束之后， 我们找到一个区间，它的计数器值小于区间大小(67108864)， 说明了这一段里面一定有数字是文件中所不包含的。然后我们单独处理这个区间即可。接下来我们就可以用Bit Map算法了。申请长度为67108864的bitArr，记为bitArr[0..67108863]，我们再遍历一遍数据， 把落在这个区间的数对应的位置1(当然数据要经过处理，即落在区间i的数num，则bitArr[num-67108864i]=1)。 最后我们找到这个区间中第一个为0的位，其对应的数就是一个没有出现在该文件中的数。
再比如：
2.5亿个整数中找出不重复的整数的个数，内存空间不足以容纳这2.5亿个整数。
将bit-map扩展一下，用2bit表示一个数即可，00表示未出现，01表示出现一次，10表示出现2次及以上，在遍历这些数的时候，如果对应位置的值是00，则将其置为01；如果是01，将其置为10；如果是10，则保持不变。或者我们不用2bit来进行表示，我们用两个bit-map即可模拟实现这个2bit-map，都是一样的道理。
2.4 堆(Heap)
实现可以看排序算法
概念：堆是一种特殊的二叉树，具备以下两种性质
1）每个节点的值都大于等于（或者都小于等于，称为小顶堆或最小堆）其子节点的值，称为大顶堆(或最大堆)。
2）树是完全二叉树，并且最后一层的树叶都在最左边
一个典型的堆结构：
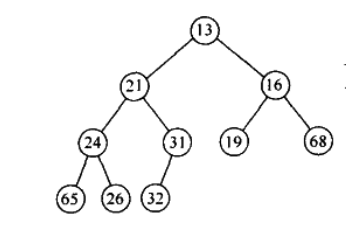
插入和删除的时间复杂度O(logn)
适用范围
海量数据前n大(最小堆，不用最大堆是为了保证我们只操作堆顶元素)或者前n小(最大堆)或者中位数(双堆，一个最大堆与一个最小堆结合)，并且n比较小，堆可以放入内存。
比如海量数据求前n小，利用大顶堆，我们比较当前元素与最大堆里的最大元素(即堆顶元素)，如果它小于最大元素，则应该替换那个最大元素，并调整堆的结构，持续这一过程，最后得到的n个元素就是最小的n个，这样可以扫描一遍即可得到所有的前n小元素，效率很高，具体算法：找到无序数组中最小的k个数。
比如海量数据求前n大，利用小顶堆，我们比较当前元素与最小堆里的最小元素(即堆顶元素)，如果它大于最小元素，则应该替换那个最小元素，并调整堆的结构，持续这一过程，最后得到的n个元素就是最大的n个。
双堆求中位数：
1、创建两个堆（一个大顶堆、一个小顶堆），并设置两个变量分别记录两个堆的元素的个数；
2、假定变量mid用来保存中位数，取第一个元素，赋值给mid，作为初始的中位数；
3、依次遍历后面的每一个数据，如果比mid小，则插入大顶堆；否则插入小顶堆，并调整堆的结构；
4、如果大顶堆和小顶堆上的数据之差的绝对值为2，则将mid插入到元素个数较少的堆中，然后从元素个数较多的堆中删除根节点，并将根节点赋值给mid；
5、重复步骤3和4，直到所有的数据遍历结束；
此时，mid保存了一个数，再加上两个堆中保存的数，就构成了给定数据的集合。
如果两个堆中元素个数相等，则mid即为最终的中位数；否则，元素较多的堆的根节点元素与mid的和求平均值，即为最终的中位数。时间复杂度：nlog(n)
2.5 双层桶划分
双层桶划分不是一种数据结构，而是一种算法设计思想，类似于分治思想。面对大量的数据我们无法处理的时候，可以将其分成一个个小的单元，然后根据一定的策略来处理这些小单元，从而达到目的。
基本原理及要点：因为元素范围很大，不能利用直接寻址表，所以通过多次划分，逐步确定范围，最后在一个可以接受的范围内进行操作。可以通过多次缩小，双层只是一个形式，分治才是其根本（只是“只分不治”）。
常规方法：把大文件通过哈希函数分配到不同的机器，或者通过哈希函数把大文件拆成小文件，一直进行这种划分，直到划分的结果满足资源限制的要求(即分流)。
适用范围：
第k大，中位数，不重复或重复的数字
2.6 数据库优化法
2.6.1 索引
Mysql索引
索引是对数据库表中一列或多列的值进行排序的一种结构，使用索引可快速访问数据库表中的特定信息。
数据库索引好比是一本书前面的目录，能加快数据库的查询速度。
例如这样一个查询：select * from table1 where id=44。如果没有索引，必须遍历整个表，直到ID等于44的这一行被找到为止；有了索引之后(必须是在ID这一列上建立的索引)，直接在索引里面找44（也就是在ID这一列找），就可以得知这一行的位置，也就是找到了这一行，可见，索引是用来定位的。
优点：
第一，通过创建唯一性索引，可以保证数据库表中每一行数据的唯一性。
第二，可以大大加快数据的检索速度，这也是创建索引的最主要的原因。
第三，可以加速表和表之间的连接(快速查询到需要连接的数据行)，特别是在实现数据的参考完整性方面特别有意义。
第四，在使用分组和排序子句进行数据检索时，同样可以显著减少查询中分组和排序的时间。
第五，通过使用索引，可以在查询的过程中，使用优化隐藏器，提高系统的性能。
缺点：
第一，创建和维护索引要耗费时间，这种时间随着数据量的增加而增加。
第二，增加了数据库的存储空间。
第三，当对表中的数据进行增加、删除和修改的时候，索引也要动态的维护，这样就降低了数据的维护速度。
一般来说，应该在这些列上创建索引：
- 在经常需要搜索的列上，可以加快搜索的速度；
- 在作为主键的列上，强制该列的唯一性和组织表中数据的排列结构；
- 在经常用在连接的列上，这些列主要是一些外键，可以加快连接的速度；
- 在经常需要根据范围进行搜索或者需要排序的列上创建索引，因为索引已经排序，其指定的范围是连续的；
- 在经常使用WHERE子句的列上面创建索引，加快条件的判断速度。
2.6.2 缓存机制
配置缓存可以有效的降低数据库查询读取次数，从而缓解数据库服务器压力。
2.6.3 数据分区
对海量数据进行分区，以降低需要处理的数据规模。比如，针对按年存取的数据，可以按年进行分区。
2.6.4 切表
分表包括两种方式：横向分表和纵向分表，其中，横向分表比较有使用意义，故名思议，横向切表就是指把记录分到不同的表中，而每条记录仍旧是完整的（纵向切表后每条记录是不完整的），例如原始表中有100条记录，我要切成2个表，那么最简单也是最常用的方法就是ID取摸切表法，本例中，就把ID为1,3,5,7。。。的记录存在一个表中，ID为2,4,6,8,。。。的记录存在另一张表中。虽然横向切表可以减少查询强度，但是它也破坏了原始表的完整性，如果该表的统计操作比较多，那么就不适合横向切表。横向切表有个非常典型的用法，就是每个用户的用户数据一般都比较庞大，但是每个用户数据之间的关系不大，因此这里很适合横向切表。最后，要记住一句话就是：分表会造成查询的负担，因此在数据库设计之初，要想好是否真的适合切表的优化。
2.6.5 分批处理
对海量数据进行分批处理，再对处理后的数据进行合并操作，分而治之。
2.6.6 用排序来取代非顺序存取
磁盘存取臂的来回移动使得非顺序磁盘存取变成了最慢的操作，尽量保证存取数据的有序性，保证数据良好的局部性。
2.6.7 日志分析
在数据库运行了较长一段时间以后，会积累大量的LOG日志，其实这里面的蕴涵的有用信息还是很多的。通过分析日志，可以找到系统性能的瓶颈，从而进一步寻找优化方案。
2.7 倒排索引(搜索引擎之基石)
倒排索引（英语：Inverted index），也常被称为反向索引、置入档案或反向档案，被用来存储在全文搜索下某个单词在一个文档或者一组文档中的存储位置的映射。它是目前搜索引擎公司对搜索引擎最常用的存储方式。
有两种不同的反向索引形式：
- 一条记录的水平反向索引：包含每个引用单词的文档的列表。
- 一个单词的水平反向索引：包含单词的文档列表和每个单词在一个文档中的位置。
后者的形式提供了更多的兼容性（比如短语搜索），但是需要更多的时间和空间来创建。
例如现在我们要对三篇文档建立索引(实际应用中，文档的数量是海量的)：
文档1(D1)：中国移动互联网发展迅速
文档2(D2)：移动互联网未来的潜力巨大
文档3(D3)：中华民族是个勤劳的民族
那么文档中的词典集合为：{中国，移动，互联网，发展，迅速，未来，的，潜力，巨大，中华，民族，是，个，勤劳}
建好的索引如下图：
在上面的索引中，存储了两个信息，文档号和出现的次数。建立好索引以后，我们就可以开始查询了。例如现在有一个Query是”中国移动”。首先分词得到Term集合{中国，移动}，查倒排索引，分别计算query和d1,d2,d3的距离。倒排索引建立好以后，就不需要再检索整个文档库，而是直接从字典集合中找到“中国”和“移动”，然后遍历后面的列表直接计算。
2.8 外排序
当待排序的对象数目特别多时，在内存中不能一次处理，必须把它们以文件的形式存放于外存，排序时再把他们一部分一部分的调入内存进行处理，这种方式就是外排序法。
基本原理及要点：
外部排序的两个独立阶段：
1）首先按内存大小，将外存上含n个记录的文件分成若干长度为L的子文件或段。依次将子文件读入内存并利用有效的内部排序对他们进行排序，并将排序后得到的有序子文件重新写入外存，通常称这些子文件为归并段。
2）对这些归并段进行逐趟归并，使归并段逐渐由小到大，最后在外存上形成整个文件的单一归并段，也就完成了文件的外排序。
适用范围：
大数据的排序，去重
一个典型实现：
假设文件被分成L段子文件，需要将所有数据从大到小进行排序（即先将最大的输出，再输出第二大的，直到所有元素的顺序被获得）。
（1）依次读入每个文件块，在内存中对当前文件块进行排序（应用恰当的内排序算法），并将排序后的结果直接写入外存文件（分别写到不同的子文件）。此时，每块文件相当于一个由大到小排列的有序队列。
（2）接下来进行多路归并排序，在内存中建立一个L个元素的大顶堆（注意这里的要求不仅仅是要获得topK，还要按照从大到小的排序输出，所以没使用小顶堆），建堆的过程就是把L块文件中每个文件的队列头（每个文件的最大值）依次加入到堆里，并调整成大顶堆。
（3）弹出堆顶元素，如果堆顶元素来自第i块（怎么知道堆顶元素来自哪一块？可以在内存中建立一个hashMap，以第几个子文件为key，以最近一个加入的元素为value，每次新加入元素则更新value），则从第i块文件中补充一个元素到大顶堆，并调整大顶堆结构。弹出的元素暂存至临时数组。
（4）当临时数组存满时，将数组写至磁盘，并清空数组内容。
（5）重复过程（3）、（4），直至所有文件块读取完毕。
2.9 Trie 树
读音：[t'ri:]
基本原理及要点：
Trie树也称字典树，它的优点是：利用字符串的公共前缀来降低存储的空间开销和查询的时间开销。 在字符串查找、统计、排序、前缀匹配等方面应用很广泛。
它有3个基本性质：
- 根节点不包含字符，除根节点外每一个节点都只包含一个字符。
- 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。
- 每个节点的所有子节点包含的字符都不相同。
比如：字符串abc,bd,dda
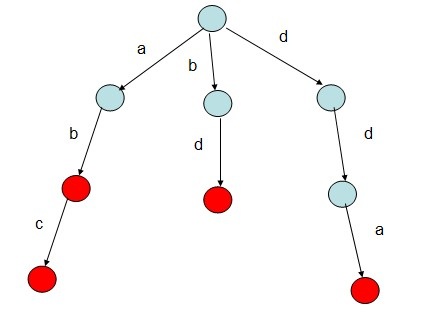
适用范围：
数据量大，重复多，但是数据种类小可以放入内存
问题实例：
1).有10个文件，每个文件1G， 每个文件的每一行都存放的是用户的query，每个文件的query都可能重复。要你按照query的频度排序 。
2).1000万字符串，其中有些是相同的(重复),需要把重复的全部去掉，保留没有重复的字符串。请问怎么设计和实现？
3).寻找热门查询：查询串的重复度比较高，虽然总数是1千万，但如果除去重复后，不超过3百万个，每个不超过255字节。
实现代码，大量递归的应用：
import java.util.ArrayList;
import java.util.Iterator;
import java.util.List;
public class Trie {
private TrieNode root = new TrieNode();
protected class TrieNode {
protected int words; //以此字符为结尾的单词的个数
protected int prefixes; //以此字符(包括此字符)的所有祖先字符组成的字符串为前缀的单词个数
protected TrieNode[] childNodes; //此节点的所有子节点
public TrieNode() {
this.words = 0;
this.prefixes = 0;
childNodes = new TrieNode[26];
for (int i = 0; i < childNodes.length; i++) {
childNodes[i] = null;
}
}
}
/**
* 获取tire树中所有的词
*/
public List<String> listAllWords() {
List<String> words = new ArrayList<String>();
TrieNode[] childNodes = root.childNodes;
for (int i = 0; i < childNodes.length; i++) {
if (childNodes[i] != null) {
String word = "" + (char) ('a' + i);
depthFirstSearchWords(words, childNodes[i], word);
}
}
return words;
}
private void depthFirstSearchWords(List<String> words, TrieNode trieNode, String wordSegment) {
if (trieNode.words != 0) {
words.add(wordSegment);
}
TrieNode[] childNodes = trieNode.childNodes;
for (int i = 0; i < childNodes.length; i++) {
if (childNodes[i] != null) {
String newWord = wordSegment + (char) ('a' + i);
depthFirstSearchWords(words, childNodes[i], newWord);
}
}
}
/**
* 计算指定前缀单词的个数
*/
public int countPrefixes(String prefix) {
return countPrefixes(root, prefix);
}
private int countPrefixes(TrieNode trieNode, String prefixSegment) {
if (prefixSegment.length() == 0) {
return trieNode.prefixes;
}
char c = prefixSegment.charAt(0);
int index = c - 'a';
if (trieNode.childNodes[index] == null) {
return 0;
} else {
return countPrefixes(trieNode.childNodes[index], prefixSegment.substring(1));
}
}
/**
* 计算完全匹配单词的个数
*/
public int countWords(String word) {
return countWords(root, word);
}
private int countWords(TrieNode trieNode, String wordSegment) {
if (wordSegment.length() == 0) {
return trieNode.words;
}
char c = wordSegment.charAt(0);
int index = c - 'a';
if (trieNode.childNodes[index] == null) {
return 0;
} else {
return countWords(trieNode.childNodes[index], wordSegment.substring(1));
}
}
/**
* 向tire树添加一个词
*/
public void addWord(String word) {
addWord(root, word);
}
private void addWord(TrieNode trieNode, String word) {
if (word.length() == 0) {
trieNode.words++;
} else {
trieNode.prefixes++;
char c = word.charAt(0);
c = Character.toLowerCase(c);
int index = c - 'a';
if (trieNode.childNodes[index] == null) {
trieNode.childNodes[index] = new TrieNode();
}
addWord(trieNode.childNodes[index], word.substring(1));
}
}
/**
* 返回指定字段前缀匹配最长的单词。
*/
public String getMaxMatchWord(String word) {
String s = "";
String temp = "";// 记录最近一次匹配最长的单词
char[] w = word.toCharArray();
TrieNode trieNode = root;
for (int i = 0; i < w.length; i++) {
char c = w[i];
c = Character.toLowerCase(c);
int index = c - 'a';
if (trieNode.childNodes[index] == null) {// 如果没有子节点
if (trieNode.words != 0)// 如果是一个单词，则返回
return s;
else
// 如果不是一个单词则返回null
return null;
} else {
if (trieNode.words != 0){
temp = s;
}
s += c;
trieNode = trieNode.childNodes[index];
}
}
// trie中存在比指定单词更长（包含指定词）的单词
if (trieNode.words == 0)//
return temp;
return s;
}
public static void main(String args[]){
Trie trie = new Trie();
trie.addWord("abcedfddddddd");
trie.addWord("a");
trie.addWord("ba");
trie.addWord("abce");
trie.addWord("abce");
trie.addWord("abcedfdddd");
trie.addWord("abcef");
String maxMatch = trie.getMaxMatchWord("abcedfddd");
System.out.println("最大前缀匹配的单词："+maxMatch);
List<String> list = trie.listAllWords();
Iterator<String> listiterator = list.listIterator();
System.out.println("所有字符串列表：");
while (listiterator.hasNext()) {
String s = (String) listiterator.next();
System.out.println(s);
}
int count = trie.countPrefixes("ab");
int count1 = trie.countWords("abce");
System.out.println("以ab为前缀的单词数："+ count);
System.out.println("单词abce的个数为：" + count1);
}
}
2.10 分布式处理 MapReduce
云计算的核心技术之一，是一种简化并行计算的分布式编程模型。
基本原理及要点：
其核心操作为Map和Reduce。Map(映射)：将数据通过 Map程序映射到不同的区块。Reduce(化简)：将不同的区块划分到不同的机器上进行并行处理。最后再对每台机器上的结果进行整合。即数据划分，结果规约。
MapReduce实例：上千万或亿数据，统计其中出现次数最多的前N个数据。
讲解：首先可以根据数据值或者把数据hash后的值，按照范围划分到不同的子机器，最好让数据划分后可以一次性读入内存，这样不同的子机器负责处理各自的数值范围。得到结果后，各个子机器只需拿出各自的出现次数最多的前N个数据，然后汇总，选出所有的数据中出现次数最多的前N个数据。
适用范围：
数据量很大(通常大于1TB)
三、经典题目
3.1 top K问题
海量数据中找出出现频度最高的前K的数或者字符串，或者海量数据中找出最大的前K个数。
如何选择hash函数分流：
1、可以根据数据值或者把数据hash(md5)后的值，按照范围划分到不同的子集，但是计算md5代价是比较高的，可以考虑其他比较简单的hash。一般应用查询的是字符串，关于String的hash函数，由于字符串计算hashCode类似于31进制转10进制，因此7个左右的字符（接近25*25*2^5...，不用32的原因是最后算的值有效位太少）就可以达到最大int值，然后利用hashCode的低16位和高16位异或，可见自学Java HashMap源码，再%表长，可以有效分流。
2、直接hash(url)%1000这种形式说明，如果分流后还是一些集合很大，则再次分流。
针对top K类问题，通常比较好的方案是分治+Trie树/HashMap+小顶堆，即hash映射分流 + hashMap统计 + 小顶堆求topK，即先将数据集按照Hash映射分解成多个小数据集，然后使用Trie树或者HashMap统计每个小数据集中的query词频，之后用小顶堆求出每个数据集中出现频率最高的前K个数，最后在所有top K中求出最终的top K。当然也可以：分流到不同机器+Trie树/HashMap+小顶堆，即先将数据集按照Hash方法分解成多个小数据集，然后分流到不同的机器上，具体多少台机器由面试官限制决定。对每一台机器，如果分到的数据量依然很大，比如内存不够或者其他问题，可以再用hash函数把每台机器的分流文件拆成更小的文件处理。然后使用Trie树或者Hash统计每个小数据集中的query词频，之后用小顶堆求出每个数据集中出现频率最高的前K个数，最后在所有top K中求出最终的top K。
eg：有1亿个浮点数，如果找出其中最大的10000个？
第一种是将数据全部排序，然后在排序后的集合中进行查找，最快的排序算法的时间复杂度一般为O（nlogn），如快速排序。但是在32位的机器上，每个float类型占4个字节，1亿个浮点数就要占用(4B*10^8=0.4GB)400MB的存储空间，对于一些可用内存小于400M的计算机而言，很显然是不能一次将全部数据读入内存进行排序的。其实即使内存能够满足要求，该方法也并不高效，因为题目的目的是寻找出最大的10000个数即可，而排序却是将所有的元素都排序了，做了很多的无用功。
第二种方法是分治+快排变体法，将1亿个数据分成100份，每份100万个数据，找到每份数据中最大的10000个，最后在剩下的100 * 10000个数据里面找出最大的10000个。如果100万数据选择足够理想，那么可以过滤掉1亿数据里面99%的数据。100万个数据里面查找最大的10000个数据的方法如下：用快速排序的方法，首先，随便选一个中轴，比他大的数据放到右边，比他小的放到左边，如果大的那堆个数N大于10000个，继续对大堆快速排序一次分成2堆。。。如果大堆个数N小于10000个，就在小的那堆里面快速排序一次，找第10000-N大的数字；递归以上过程，就可以找到第10000大的数（利用快排的变体找到第k大，平均时间复杂度O(N)，可以看找到无序数组中第k个最小的数），然后一遍遍历就可以找到前10000大。此种方法需要每次的内存空间为\(10^6*4B=4MB\)，一共需要101次这样的比较。
第三种方法是Hash去重+最小堆法。如果这1亿个数里面有很多重复的数，先通过hashMap，把这1亿个数字去重复，这样如果重复率很高的话，会减少很大的内存用量，从而缩小运算空间，然后通过分治+最小堆法或直接最小堆法查找最大的10000个数。
第四种方法直接最小堆法。首先读入前10000个数来创建大小为10000的最小堆，建堆的时间复杂度为O（m）（m为数组的大小即为10000），然后遍历后续的数字，并与堆顶（最小）数字进行比较。如果比最小的数小，则继续读取后续数字；如果比堆顶数字大，则替换堆顶元素并重新调整堆为最小堆。重复整个过程直至1亿个数全部遍历完为止。然后按照中序遍历的方式输出当前堆中的所有10000个数字。对每一个输入，堆调整的时间复杂度是O(logm)，最终时间复杂度为：1次建堆时间+n次堆调整时间=O(m+nlogm)=O(nlogm)，空间复杂度是10000（常数）。
实际运行：
实际上，最优的解决方案应该是最符合实际设计需求的方案，在实际应用中，可能有足够大的内存，那么直接将数据扔到内存中一次性处理即可，也可能机器有多个核，这样可以采用多线程处理整个数据集。
下面针对不同的应用场景，分析了适合相应应用场景的解决方案。
（1）单机+单核+足够大内存
如果需要查找10亿个查询词（每个占8B）中出现频率最高的10个，每个查询词占8B，则10亿个查询词所需的内存大约是10^9 * 8B=8GB内存。如果有这么大内存，直接在内存中先用HashMap求出每个词出现的频率，然后用小顶堆求出频率最大的10个词。
（2）单机+多核+足够大内存
这时可以直接在内存中使用Hash方法将数据划分成n个partition，每个partition交给一个线程处理，线程的处理逻辑同（1）类似，最后一个线程将结果归并。
该方法存在一个瓶颈会明显影响效率，即数据倾斜。每个线程的处理速度可能不同，快的线程需要等待慢的线程，最终的处理速度取决于慢的线程。而针对此问题，解决的方法是，将数据划分成c×n个partition（c>1），每个线程处理完当前partition后主动取下一个partition继续处理，直到所有数据处理完毕，最后由一个线程进行归并。
（3）单机+单核+受限内存
这种情况下，需要用hash函数将原数据文件映射到一个一个小文件，如果小文件仍大于内存大小，继续采用Hash的方法对数据文件进行分割，直到每个小文件小于内存大小，这样每个文件可放到内存中处理。采用（1）的方法依次处理每个小文件。
（4）多机+受限内存
这种情况，为了合理利用多台机器的资源，可用hash函数将原数据文件映射到一个一个小文件，然后分发到多台机器上，每台机器采用（3）中的策略解决本地的数据，最后将所有机器处理结果汇总，并利用小顶堆求出频率最大的10个词。
从实际应用的角度考虑，（1）（2）（3）（4）方案并不可行，因为在大规模数据处理环境下，作业效率并不是首要考虑的问题，算法的扩展性和容错性才是首要考虑的。算法应该具有良好的扩展性，以便数据量进一步加大（随着业务的发展，数据量加大是必然的）时，在不修改算法框架的前提下，可达到近似的线性比；算法应该具有容错性，即当前某个文件处理失败后，能自动将其交给另外一个线程继续处理，而不是从头开始处理。
top K问题很适合采用MapReduce框架解决，用户只需编写一个Map函数和两个Reduce 函数，然后提交到Hadoop（采用Mapchain和Reducechain）上即可解决该问题。具体而言，就是首先根据数据值或者把数据hash(MD5)后的值按照范围划分到不同的机器上，最好可以让数据划分后一次读入内存，这样不同的机器负责处理不同的数值范围，实际上就是Map。得到结果后，各个机器只需拿出各自出现次数最多的前N个数据，然后汇总，选出所有的数据中出现次数最多的前N个数据，这实际上就是Reduce过程。对于Map函数，采用Hash算法，将Hash值相同的数据交给同一个Reduce task；对于第一个Reduce函数，采用HashMap统计出每个词出现的频率，对于第二个Reduce 函数，统计所有Reduce task，输出数据中的top K即可。
直接将数据均分到不同的机器上进行处理是无法得到正确的结果的。因为一个数据可能被均分到不同的机器上，而另一个则可能完全聚集到一个机器上，同时还可能存在具有相同数目的数据。
以下是一些经常被提及的该类问题。
（1）有一个1G大小的文件，里面每一行是一个词，词的大小不超过16字节，内存限制大小是1M。返回频数最高的100个词。
方案1：
顺序读文件，对于每个词x，取hash(x)%5000，然后按照该值存到5000个小文件中。这样每个文件大概是200k左右。如果其中有的文件超过了1M大小，还可以按照类似的方法继续往下分，直到分解得到的小文件的大小都不超过1M。对每个小文件，统计每个文件中出现的词以及相应的频率（可以采用trie树/hash_map等），并取出出现频率最大的100个词（可以用含100个结点的最小堆），并把100词及相应的频率存入文件，这样又得到了5000个文件。下一步就是把这5000个文件进行归并（类似于归并排序）的过程了。
（2）搜索的输入信息是一个字符串，统计300万条输入信息中最热门的前10条，每次输入的一个字符串为不超过255B，内存使用只有1GB。
典型的Top K算法，第一步、先对这批海量数据预处理，在O（N）的时间复杂度内用HashMap完成统计；第二步、借助最小堆找出Top K，时间复杂度为N‘logK。 即最终的时间复杂度是：O（N） + N'*O（logK），（N为1000万，N’为300万）
（3）最大间隙问题
给定n个实数，
，求这n个实数在实轴上相邻2个数之间的最大差值，要求线性的时间算法。
最先想到的方法就是先对这n个数据进行排序，然后一遍扫描即可确定相邻的最大间隙。但该方法不能满足线性时间的要求。故采取如下方法：
- 找到n个数据中最大和最小数据max和min。
- 用n-2个点等分区间[min, max]，即将[min, max]等分为n-1个区间（前闭后开区间），将这些区间看作桶，编号为
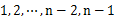，且桶i的上界和桶i+1的下界相同，即每个桶的大小相同。每个桶的大小为：
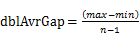，且认为将min放入第一个桶，将max放入第n-1个桶。 - 将n个数放入n-1个桶中：将每个元素x[i]分配到某个桶（编号为index），其中
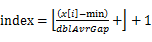，并且只需要记录分到每个桶的最大最小数据。 - 最大间隙：除最大最小数据max和min以外的n-2个数据放入n-1个桶中，由抽屉原理可知至少有一个桶是空的，又因为每个桶的大小相同，所以最大间隙不会在同一桶中出现，一定是某个桶的最小数据和另一个桶的最大数据之差，且该两桶之间的桶一定是空桶。也就是说，最大间隙在桶i的最大数据和桶j的最小数据之间产生
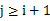。向前扫描一遍，找到所有有空桶的地方的最大间隙的最大值，一遍扫描即可完成。
3.2 重复问题
在海量数据中查找出重复出现的元素或者去除重复出现的元素也是常考的问题。针对此类问题，一般可以通过位图法实现。例如，已知某个文件内包含一些电话号码，每个号码为8位数字，统计不同号码的个数。
以下是一些经常被提及的该类问题。
（1）给定a、b两个文件，各存放50亿个url，每个url各占64字节，内存限制是4G，让你找出a、b文件共同的url？
方案1：
可以估计每个文件的大小为5G×64=320G，远远大于内存限制的4G。所以不可能将其完全加载到内存中处理。考虑采取分而治之的方法。
- 遍历文件a，对每个url求hash(url)%1000，然后根据所取得的值将url分别存储到1000个小文件（记为a0,a1,a2...a999）中，这样每个小文件的大约为300M。
- 遍历文件b，采取和a相同的方式将url分别存储到1000小文件（记为b0,b1,b2...b999）中。这样处理后，所有可能相同的url都在对应(a0-b0,a1-b1,...,a999-b999)的小文件中，不对应的小文件不可能有相同的url。然后我们只要求出1000对小文件中相同的url即可。
- 求每对小文件中相同的url时，可以把其中一个小文件的url存储到hash_set中。然后遍历另一个小文件的每个url，看其是否在刚才构建的hash_set中，如果是，那么就是共同的url，存到文件里面就可以了。
方案2：
如果允许有一定的错误率，可以使用Bloom filter，4G内存大概可以表示340亿bit。将其中一个文件中的url使用Bloom filter映射为这340亿bit，然后逐个读取另外一个文件的url，检查它是否在Bloom filter表示的集合中，如果是，那么该url应该是共同的url（注意会有一定的错误率）。
（2）在25亿个整数中找出不重复的整数，内存不足以容纳这25亿个整数。
方案1：
采用2-Bitmap（每个数分配2bit，00表示不存在，01表示出现一次，10表示多次，11无意义）进行，共需\(2^{32}*2bit=2^{30}B\)=1GB内存，还可以接受。然后扫描这2.5亿个整数，查看Bitmap中相对应位，如果是00变01，01变10，10保持不变。所有整数遍历完成后，查看bitmap，把对应位是01的整数输出即可。
方案2：
采用映射的方法，比如模1000，把整个大文件映射为1000个小文件，再找出每个小文件中不重复的整数。对于每个小文件，用hash_map(int,count)来统计每个整数出现的次数，输出即可。
（3）1000万字符串，其中有些是重复的，需要把重复的全部去掉，保留没有重复的字符串。请怎么设计和实现？
方案1：这题用trie树比较合适，hash_map也应该能行。
3.3 排序问题
一般采用位图(若为int型的数，最多\(2^{32}\),\(2^{32}*1bit=2^{30}/2B\)=0.5GB=500MB，完全可以放入内存)或者外排序。
（1）有10个文件，每个文件1G，每个文件的每一行存放的都是用户的query，每个文件的query都可能重复。要求你按照query的频度排序。
方案1：
- 顺序读取10个文件，按照hash(query)%10的结果将query写入到另外10个文件（记为a0,a1,a2...a9）中。这样新生成的文件每个的大小大约也1G（假设hash函数是随机的）。
- 找一台内存在2G左右的机器(如果可用内存很小，则分到更多的文件中)，依次对a0,a1,a2...a9用hash_map(query, query_count)来统计每个query出现的次数，然后利用快速/堆/归并排序按照出现次数进行排序。将排序好的query和对应的query_cout输出到文件中。这样得到了10个排好序的文件（记为b0,b1,b2...b9）。
- 对b0,b1,b2...b9这10个文件进行归并排序（内排序与外排序相结合）。
方案2：
一般query的总量是有限的，只是重复的次数比较多而已，可能对于所有的query，一次性就可以加入到内存了。这样，我们就可以采用trie树/hash_map等直接来统计每个query出现的次数，然后按出现次数做快速/堆/归并排序就可以了
方案3：
与方案1类似，但在做完hash，分成多个文件后，可以交给多个机器来处理，采用分布式的架构来处理（比如MapReduce），最后再进行合并。
