逻辑回归笔记总结
1. 逻辑回归模型概述
逻辑回归处理的是分类问题而不是回归问题。
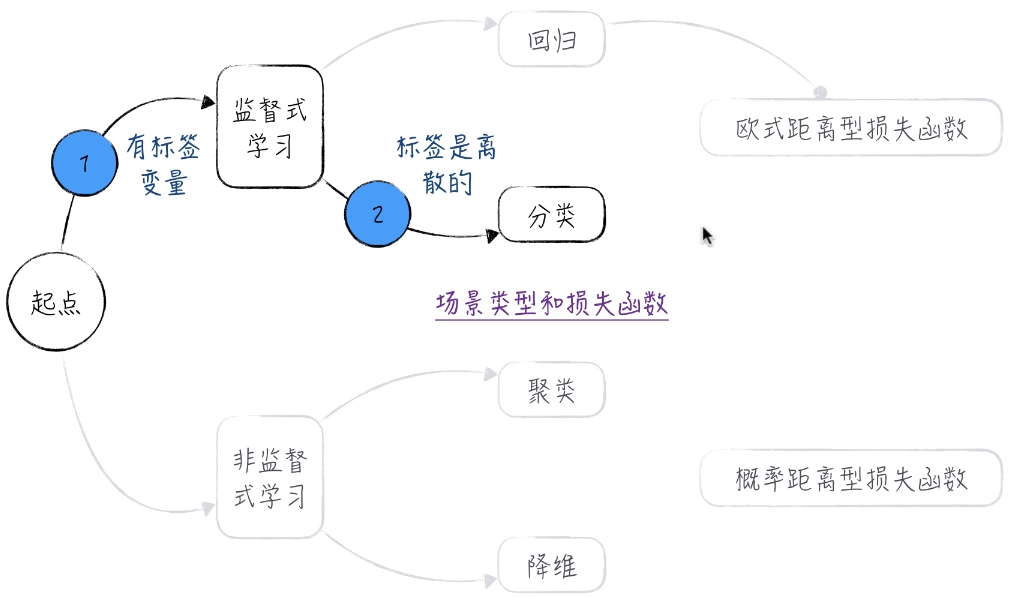
1.1 线性模型为何失效
在数学上,如果用 y 表示选择的结果,那么 y 只有两种可能的取值:0 或者 1 。这就是二元分类问题。
如果使用 线性回归 模型解决二元分类问题,我们搭建的模型就是

对于真实值来说,只有两种可能 0 或者 1。但是模型预测的值却是整个实数系。这显然就不太合理。更重要的一点是,我们假设随机变量 ε 服从正态分布。但是如果采用这个模型,我们会发现模型的误差显然不服从正态分布。也就是说 这与模型假设相矛盾。这也是最重要的原因。

首先在搭建模型的时候,我们要进行 模型假设 。然后进行一系列严谨的数学计算,而数学计算是不会出错的。所以 模型假设 是唯一的软肋,一旦它出了问题,那么结果必定不会可靠。

1.2 从线性到非线性
对于一个客户来说,我们可观测到的是 客户买或者不买商品。但购物能给消费者带来两种相反的效应。这是我们不可观测的。
正效应:满足客户的需求 等。
负效应:花费金钱 等。
如果正效应大于负效应,则购买者会购买,否则就不会购买。
这里假设 正效应 和 负效应 是拥有服从正态分布的随机变量的线性回归模型。正效应和负效应存在一种竞争的关系,正效应和负效应的差大于 0 就说明要购买。反之,则不购买。而且二者的差依然服从正态分布。因此通过 两个线性回归模型 和 一个非线性变化 就巧妙的将不可观测到的和可观测到的联系在一起。这在学术上称之为窗口效应。

根据上面讨论的,我们进行如下建模。
Probit回归模型 可以完美解决二分类问题,但是它仍然有缺点。因为它采用的是标准正态分布,而它的概率是很难计算的,在数学上很难推导。所以,取巧的办法就是找到另外一个函数,它能够近似的去代替正态分布。在数学上,这个分布就叫做 逻辑分布 。它的概率密度函数如下
 更重要的是它的累积分布函数就是大名鼎鼎的 Sigmoid 函数:
更重要的是它的累积分布函数就是大名鼎鼎的 Sigmoid 函数:
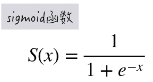
Sigmoid 函数与正态分布的累积分布函数对比图如下:
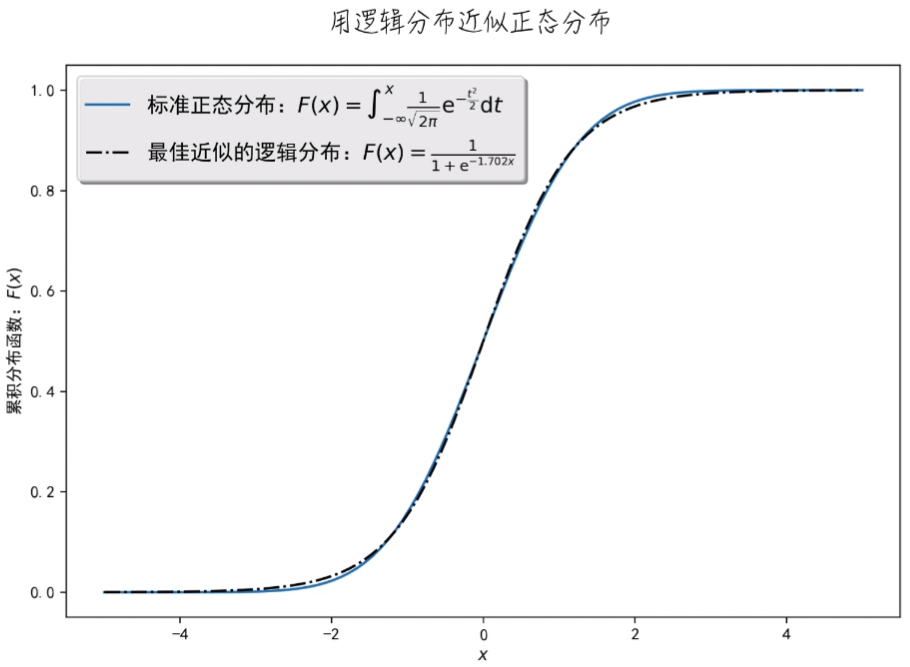
二者非常相像,我们就可以用 Sigmoid 函数这个比较简单的函数来代替复杂的正态分布函数进行计算。
所以,就可以得到 逻辑回归 公式。第二行的公式是将第一行的公式进行变换,我们能够看到 y = 1的概率除以 y = 0的概率再取对数,它得到的就是一个线性回归模型。所以,这个直观的得到了所谓的 逻辑回归模型 其实就是 线性模型加上了一层非线性变换。

1.3 逻辑回归的模型细节
在分类模型的理论讨论中,我们常常使用指示函数,其中 A 表示一个给定的集合
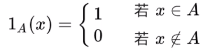
具体举一个例子,只有 y = 0 的时候,指示函数的值才为 1 ,其他全为 0 。

在机器学习领域,对于分类问题,常常用一个 n 维向量来表示数据的类别(也就是变量 y ),例子如下,当 y = 0 的时候,前者符合范围,后者不符合范围。所以为(1,0) 。
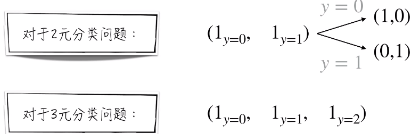
1.3.1 统计学角度:似然函数
逻辑回归的直接建模对象是 y = 1 的概率。也就是下面的式子:
![]()
结合变量的真实值,可以得到数据出现的概率。下面的式子很巧妙,可以把 y 的概率分布写成各个离散点概率分布的公式:
![]()
根据这个公式,就可以定义逻辑回归的似然函数,为了书写方便,首先定义 H(x),其实就是 y = 1 的概率:
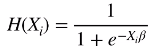
另外,yi 之间是相互独立的关系。因此,一系列 y 的联合分布概率也就等于每一点的概率相乘。那么套用第二个巧妙的式子,就可以得到下面的似然函数:
![]()
得到似然函数后,就可以根据最大似然估计法,得到参数模型的估计值:

唯一需要注意的是,和线性回归一样。采用自然对数的方法将乘法问题转换成了加法问题,以便于计算。
1.3.2 机器学习:损失函数
和线性回归一样,我们想定义模型在每一点的损失,然后定义出整个模型的损失函数,最后再根据最小损失函数的原则来得到模型参数的估计值。
具体来说,y 是随机变量,根据真实值,y 的概率分布如下,这是真实的概率分布:
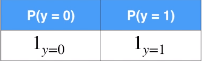
对于逻辑回归模型,y 的概率分布如下,这是模型预测的概率分布:

同时有了真实概率分布和预测概率分布,就可以很容易定义模型在某一点的损失。两个概率分布的差距,就是模型的损失。在数学上,可以使用 交叉熵 来衡量两个概率分布之间的差距。
举个例子,对于两个概率分布 p 和 q 来说,它们的交叉熵可以定义为:

顺便一提,交叉熵的理论基础是 KL 散度。
有了理论基础,逻辑回归的损失函数 LL 定义如下,还是定义一个 H(x) 方便表示,它是 y = 1 的概率:
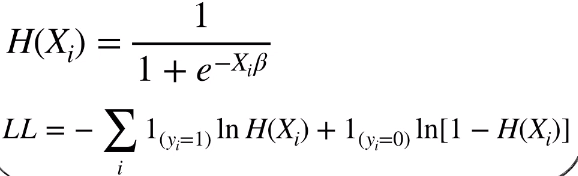
前面的一项是 y = 1 时,真实概率分布和预测概率分布的乘积。
后面的一项是 y = 0 时,真实概率分布和预测概率分布的乘积。
那么细心的你或许会注意到,我们采用最小损失的原则来得到模型参数的估计公式。和上面统计学使用最大似然估计法得到的公式是一样的。这说明,两种不同的角度,完全不同的方法,得到的结果是一样的。
又该掏出那张图了。总结一下。

1.3.3 最终预测结果
逻辑回归模型的直接结果是 y = 1 的概率。为了得到最终类别的预测,需要做进一步的转换。具体来讲:
1. 人为选择一个阈值 Alpha (二元分类问题 一般 Alpaha 都等于 0.5 )
2. 当预测的 y = 1 的概率大于这个阈值时,最终的预测结果就等于 1 。否则为 0 。
数学公式如下:

2. 如何评估分类模型的效果
建模背景如下图:

2.1 查准率和查全率
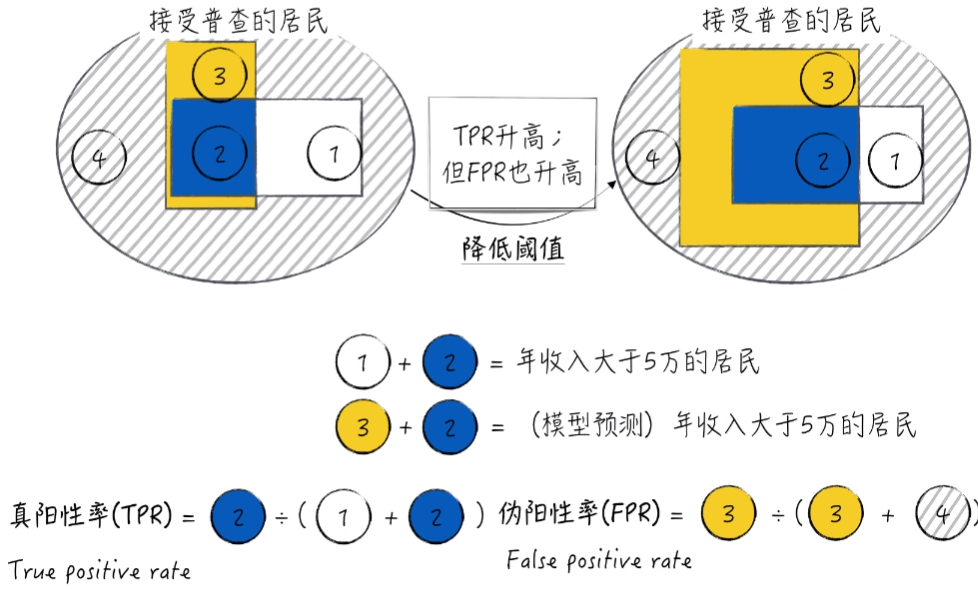
为了方便理解,将数据进行可视化。1号区域加2号区域代表真实情况下,年收入大于5万的居民。2号区域加3号区域代表模型预测的年收入大于5万的居民。2区域代表模型和实际都大于5万的居民,也就是模型预测正确的部分。3区域代表模型预测错误的部分,也就是模型预测大于5万但真实值不到5万的部分。

查准率(precision)代表 模型预测年收入大于5万的居民中有多少真实值也大于5万(也就是预测正确占所有预测结果的百分比)。
希望预测结果 “精准”。

查全率(recall)代表 真实年收入大于5万的居民中有多少模型预测也大于5万(也就是预测正确占所有真实结果的百分比)。
希望预测结果 “完整”。
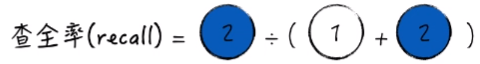
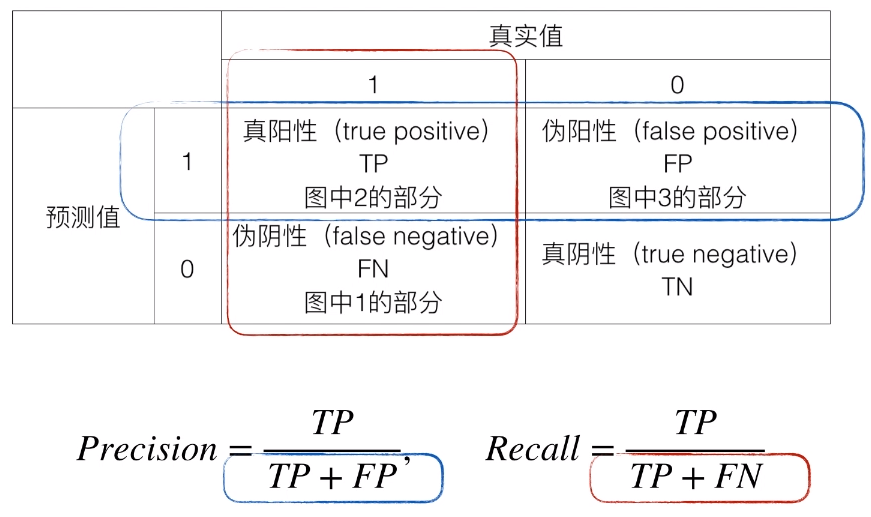
下面来看看在数学上查准率(precision)和查全率(recall)的严谨定义,首先引入混淆矩阵。
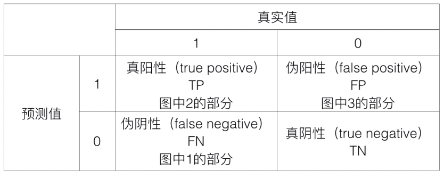
二者公式如下:
![]()
当然,从概率的角度来说,可以认为查准率(precision)和查全率(recall)是两个条件概率。
查准率(precision)表示模型预测等于 1 时,真实值等于 1 的条件概率。
查全率(recall)表示真实值等于 1 时,模型预测值等于 1 的条件概率。
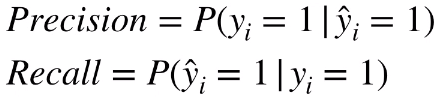
2.2 综合指标 F-score
由于查准率与查全率往往存在 “此消彼长”的现象。也就是说一个增大,另一个减小。举个例子,模型的结果是由阈值来进行控制。如果我们降低阈值,那么就会出现提高查全率,降低查准率的结果:

换句话说,对于预测结果,单个指标的意义非常有限。
极端地,预测所有居民的年收入都大于5万,那么
1. 查全率达到100%。即所有正确情况全部预测出来。
2. 但预测结果没有意义,因为所有小于5万的情况也都预测为大于5万。
所以定义综合指标就尤为重要。数学上,定义 F1 score 来综合查准和查全两个指标:
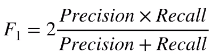
但是在现实生活中,不同场景下,对查准查全的重视程度是不一样的。有时候更注重查准,有时候更注重查全。在数学上就定义了 Fbeta score 来满足这样的需求。

Beta 值是一个权值。如果它越接近于 0 ,那么就更接近于查准率(越看重查准率)。如果它越接近正无穷,那么就更接近于查全率(越看重查全率)。

Fbeta score 不仅仅是一个评估模型的指标,我们甚至可以用它来选择更好的模型。
比如说 针对逻辑回归模型,可以借助 F score 来确定阈值 Alpha 的值。具体来说,首先要确定最大化的 Fbeta score (注重查准还是查全),然后找到使得 Fbeta score 达到最大值的 Alpha 的取值。
![]()
2.3 ROC曲线与AUC指标
2.3.1 ROC曲线
首先回顾一下查准率和查全率,
对于查全率(Recall)的分母来说,不管采用什么模型,它的值都是确定的,因为真实值有多少是由数据确定的,而不是模型确定的。
但是对于查准率(Precision)来说,它的分母是和模型相关的,而不是数据确定的。
总体来说,混淆矩阵我们并没有用到 TN 这个框框,因此,我们希望定义新的指标覆盖所有格子。
首先,定义了 TPR ,TPR 叫做真阳性率,其实就是查全率(Recall)。它代表对于真实值为 1 的数据,我们预测正确的概率,我们希望它越大越好。
与之相对的是 FPR,叫做伪阳性率。它代表对于真实值为 0 的数据,我们错误地将其预测成正确的概率(预测错误的概率),我们希望它越小越好。

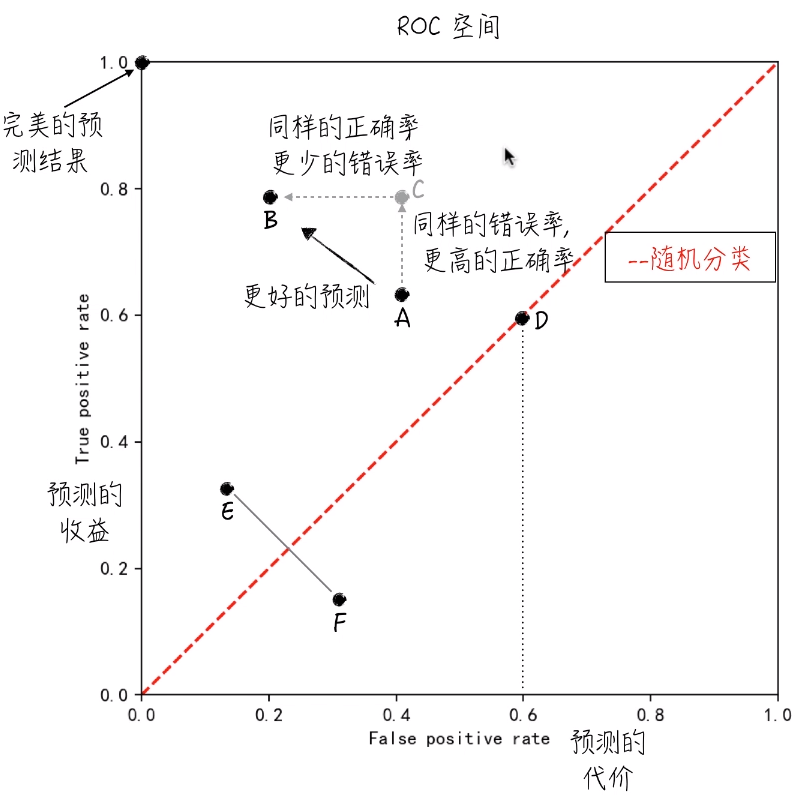
有了这两个指标,就可以定义所谓的 ROC 空间,它的横轴上是 FPR,纵轴是 TPR。
1. 对于(0,1)这个点,它被称为完美的预测结果,因为它的预测收益是 1 ,预测代价是 0 。
2. 左上方的点表示更好的预测结果,因为收益更多,代价更少。(点 A,B,C 证明了)
3. 对角线表示随机分类结果。(也就是瞎猜的结果)
比如,对于任何一点。60%的概率预测它等于 1 ,40%预测它等于 0 。(D点)
它的 FPR 和 TPR 都为0.6。所以所有不同概率乱猜就构成了这条对角线。
从模型的角度来讲,随机乱猜是最差的分类结果。所以对于所有落于随机线右下方的点(点F),我们可以仅仅认为它的预测结果颠倒了。我们只需要把点 F 预测为 1 的改为 0,0 的改为 1 。这样对调之后,就可以得到点 E 。所以,对于所有结果都不可能落到对角线的右下方。
要时刻记得,逻辑回归模型的直接预测结果是 y=1 的概率。为了得到最终的预测,还要做进一步的转换。即,人为选定阈值 Alpha。当预测的 y=1 的概率大于这个阈值,最终预测结果就等于 1 。
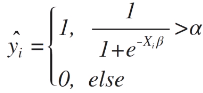
那么总结一下:
那么把阈值设定为 1 。这时候没有任何点被预测为 1 。所以它的 FPR 和 TPR 都为 0 。在图上就是在原点(0,0)。我们不断降低阈值,曲线会从(0,0)逐步往(1,1)走。当阈值为 0 时,在点(1,1)处。

同时,我们知道,点越靠近左上角,结果是越好的。所以,我们就定义了曲线下面积 AUC 。这个面积越大就说明整体更靠近左上,效果也就越好。
2.3.2 曲线下面积 AUC
根据上面要轮的结果,我们开始将 Alpha 值设置为 < 0.1 的时候,由于逻辑回归预测值全部大于等于 0.1 。根据下面的公式,模型当 Alpha < 0.1 的预测结果均为 1 。以此类推,我们得到各种 Alpha 的不同取值下模型的最终预测结果(也就是下面的蓝色区域)。
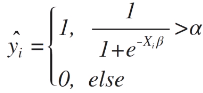
而根据 FPR 和 TPR 的定义。就可以得到最下面的表。对于 FPR 来说,它代表对于真实值为 0 的数据,我们预测错误的概率。对于 TPR 来说, 它代表对于真实值为 1 的数据,我们预测正确的概率。

将上面的 FPR 和 TPR 表格表示在 ROC 空间中。将这5个点连接起来,我们可以得到下面的图形。以及可以求出 曲线下面积AUC的面积,也就是灰色部分的面积。
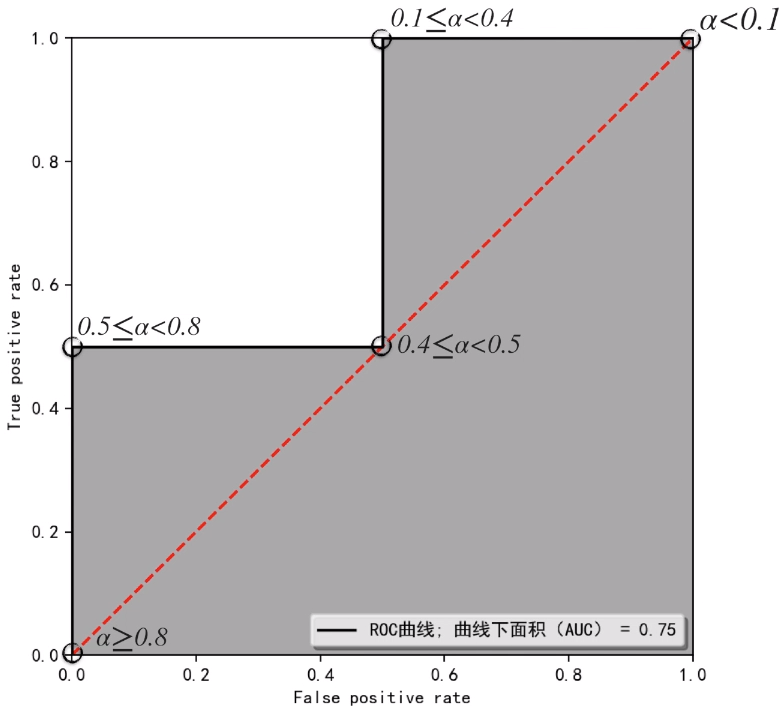
在图中,我们可知这个图的 AUC 等于 0.75 。
下面对于 AUC 的概率进行解释。
这个 0.75 表示的是,如果我们随机选择两点。K 和 L ,其中 K 点真实值为 1,L 点真实值为 0 。 对于一个模型,我们希望 K 点的打分是大于 L 点的打分的,这里的打分指的是模型预测的 y = 1 的概率。
那么 K 点预测值等于 1 的概率大于 L 点预测值等于 1 的概率的概率恰好就是 AUC 的面积。
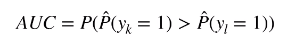
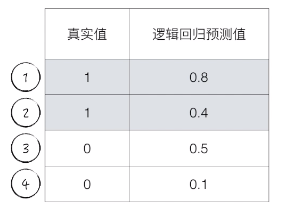
以这道题为例,当我们选择 K 点为 1 号数据点,不管我们怎么选择 L 这个点(L 可能为 3 或 4 号数据点),我们都可以得到 K 点的得分大于 L 点的得分。当我们选择 K 点为 2 号数据点,只有当 L 为 4 号数据点的时候,K 点得分才大于 L 点得分。(选择 3 号数据点时,0.5 > 0.4,所以 K 点得分小于 L 点得分)。所以在 4 种情况下,有三种情况 K 点大于 L 点。所以概率 为 3 / 4 = 0.75。这就是 AUC 的值。
3. 如何解决多元分类问题
3.1 多元逻辑回归模型
这里的多元逻辑回归和平常所说的逻辑回归有所区别。逻辑回归仅仅用于解决二元分类问题。
区别于二元分类问题,多元分类问题拥有更多的选项,并不仅仅是真假。比如说,周末选择去干什么?可以 吃饭,打游戏,逛街 等等。
解决多元分类问题,也可以借鉴二元分类问题的解决。
从隐含变量模型出发,推导出各个类别的概率(模型预测的概率)。首先定义 K 个隐含变量模型:

其中 i 指的是个体,比如说,我周末去干什么,那么 i 就指的是 “我”。
在逻辑回归中,只有前两项 Y。并且逻辑回归中,随机扰动项 ε 服从逻辑分布,也就是近似正态分布,用来代替正态分布并且好计算的那个分布。
在多元逻辑回归中,随机扰动项 ε 服从标准类型1的极端值分布,这个分布和正态分布的形状几乎是一样的,只是 “尾巴” 会比正态分布稍微厚一点点。做这个假设的目的还是在于方便数学上的计算。
接下来就可以定义第 i 个个体属于某个类别的判断逻辑。个体属于某个类别,当且仅当这个类别对它的效用最大。也就是说,举个例子,上面的 Yi,0* 是所有的 Y 最大值时,我们就认为 i 这个个体属于 0 这个类别。
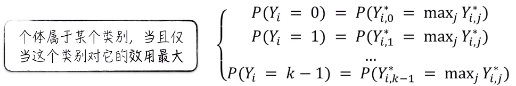
由此经过数学推导,就可以得到各个类别的概率分布。这个公式与逻辑回归得到的公式特别像。如果假设 K = 2,那么就回到了逻辑回归的场景,这里的公式和正常逻辑回归得到的公式是一样的。
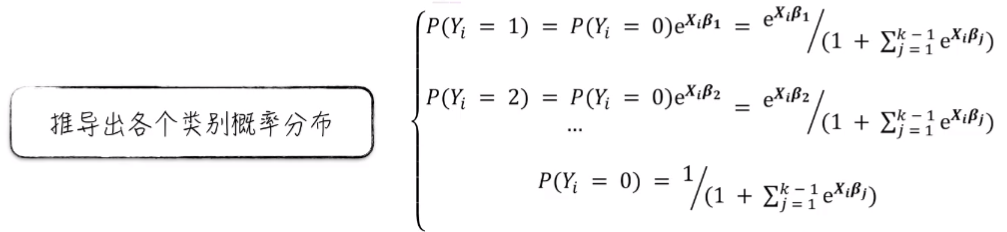
有了各个类别的概率分布,就可以推导出模型参数的估计公式。也就是模型的似然函数。真实值的一个分布概率值。和逻辑回归与线性回归一样,这个概率值是一个乘积的关系。为了方便运算,要用自然对数将其转换成一个加法的形式。
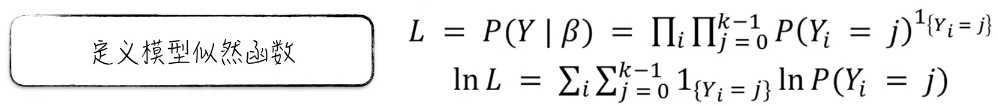
最后,利用最大似然估计法来估计模型参数。也就是说模型参数的估计值就是使 似然函数 L 达到最大值时的参数取值。
![]()
3.2 降维到二元分类问题
将多元分类问题分解为多个二元分类问题来解决。解决的方法主要有两种。
1. OvR(OvA):One-vs.-rest
2. OvO:One-vs.-one
3.2.1 OvR(OvA):One-vs.-rest
假设我们面对一个三元分类问题。有 0,1,2 三个选项。

我们将其分解成小的二元分类问题。从中分别得到 Y = 0,1,2 的概率。

但是需要注意的是,这里的概率不是真实的,只是虚假的。只是对于一种可能来说成真的概率。所以这里的三个 P(Y=0),P(Y=1),P(Y=2),的和不一定等于 1。对于这种概率,我们只选择概率值最大的,作为最终的预测结果。
![]()
3.2.2 OvO:One-vs.-one
依然假设,我们面对一个三元分类问题。

我们将其两两拿出来,让它们互相 PK 。分别用逻辑回归来解决 3 个子问题。
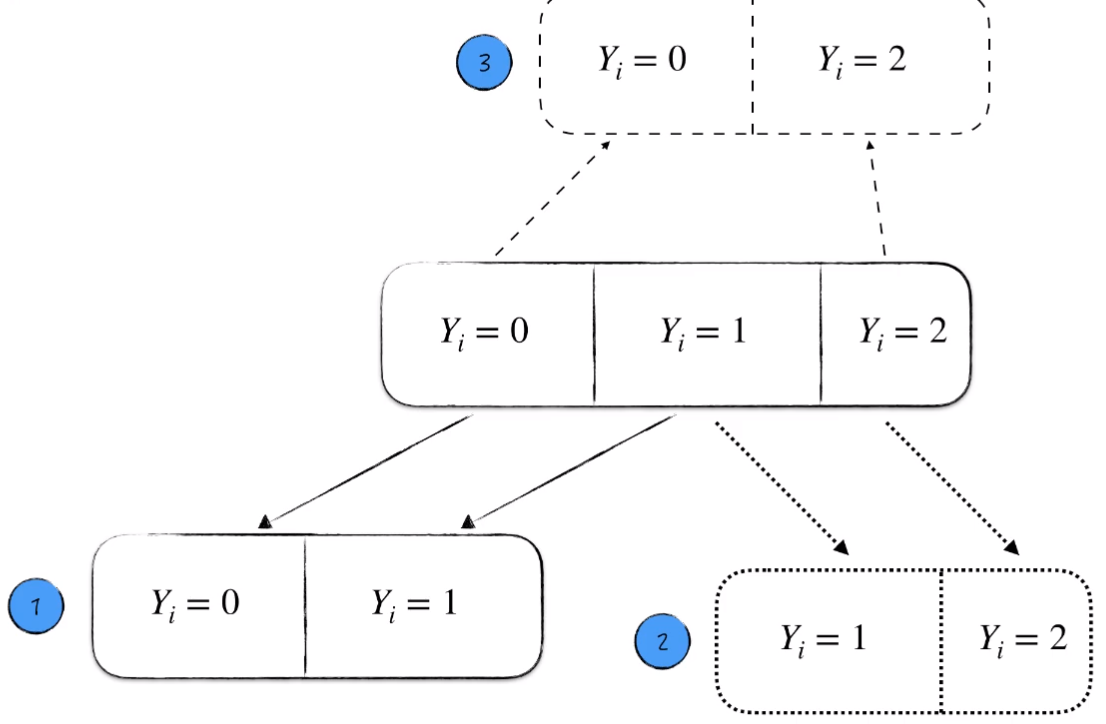
对于每一个子问题都有一个优胜者。最后 “获胜”次数最多的,作为最终预测结果。
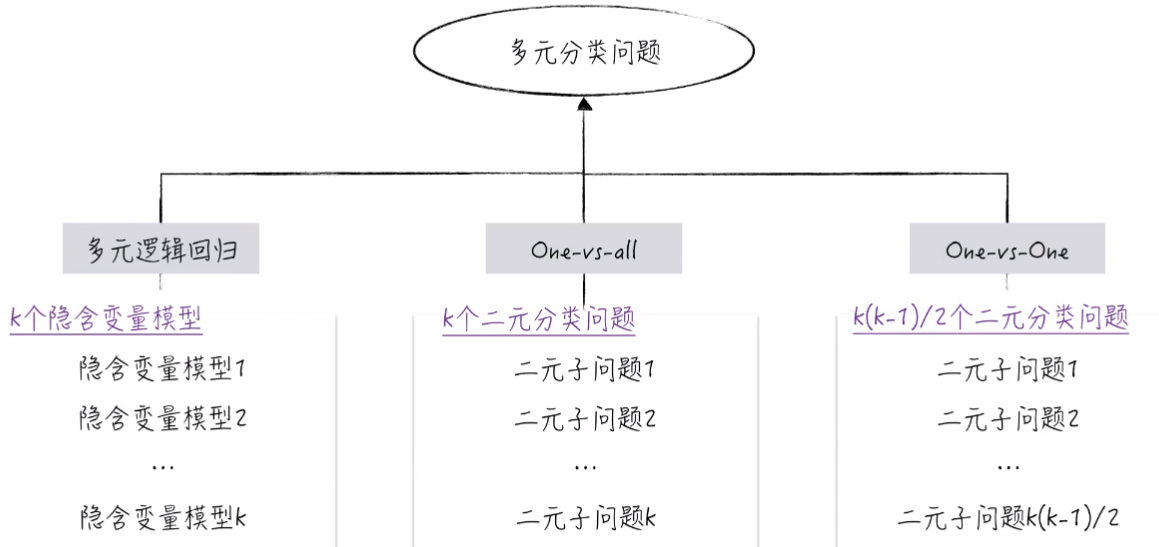
3.3 多元分类问题总结
我们可以直接使用多元逻辑回归模型,也可以降维分解成一个个二元分类问题,用逻辑回归分别解决。
4. 非均衡分类问题
4.1 非均衡数据集
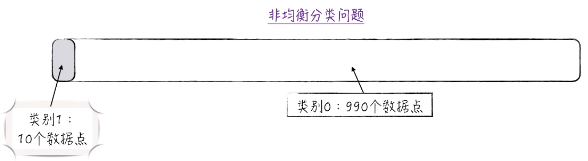
在面对分类问题时,各类别占比差距很大的数据集就是非均衡数据集。举个例子:

在实际的应用中,会经常遇到非均衡数据集,比如信贷,反欺诈,广告预测等。信贷违约的人一定是比不违约的人少得多的。违约的人占比很小。
同样的,对于多元分类问题,如果使用 OvR 策略,也容易引发 “潜在的” 非均衡数据集。
非均衡数据集会给模型搭建带来极大的困难。
4.2 准确度悖论

这个看似很直观的评估指标在面对非均衡分类问题会严重失真。
下面引入混淆矩阵:

我们很容易的得到 准确度 这个指标的数学公式。
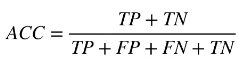
假设一个非均衡分类问题:
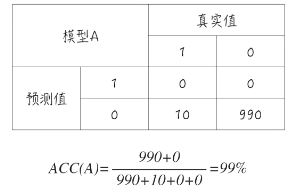
并且假设一个模型 A ,其实它并没有预测功能,因为它对所有预测结果都是 0 。所以它预测准确的是 990 个,预测错误的是 10个。对于一个这样模型,它的准确度为 99% 。这是一个相当高的数字。
对于另外一个模型 B,它有一定的辨识度,并不是所有点都预测为 0 。
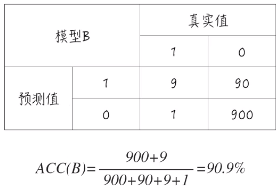
从准确度上来看,模型 B 并没有模型 A 更高。但是实际上模型 A 并没有辨识度,所有类型都预测成 0 。模型 A 并没有任何作用。这就是所谓的准确度悖论。
4.3 非均衡数据集与准确度悖论对建模的影响
首先假设一个式子

如果使用逻辑回归模型对数据进行建模,会得到非常好的结果,因为变量都完美服从逻辑分布假设。
但是,如果面对了一个非均衡数据集,结果就不一样了。
对于第一幅图,虽然原始数据类别1 的个数始终是 1000 。但是类别1 所占的比例是急剧减小的(单纯增大类别0 的个数)。如果用逻辑回归直接进行建模,就可以看到随着类别1 占比的减小,预测结果里面,类别1 的概率也是急剧减小的。到了末端,这个模型基本没有了预测效果。因为它把所有的数据点都预测为了类别0 。这也就是上面讨论的准确度悖论中的情况。
对于第二幅图,从评估指标的方面来看。虽然我们知道随着类别1 的占比减小,模型并没有预测效果。但是准确度却是不断上升的。这就是刚才讨论的准确度悖论。但是曲线下面积AUC 却是正常的表现了这个模型预测效果的逐渐下降。

总结一下:
1. 虽然 y,x1,x2 之间完美服从逻辑回归模型的假设,但数据越不均衡,模型效果越差。
2. 当面对费均衡数据集时,准确度这个评估指标会严重失真。
4.4 非均衡分类问题的解决办法
假设非均衡数据集,类别1 少,类别0 多。对于逻辑回归的参数估计公式

h(xi) 靠近 1 ,预测结果为类别1 ,反之预测结果为 0 。
对于非均衡数据集,对于类别1 ,它的损失是 -ln h(x),它想使 h(x) 靠近1 。
对于类别0 ,它的损失是 -ln[1 - h(x)] ,它想使 h(x) 靠近0 。
需要注意的是,每个点的权重都等于1 。由于类别1 附近有很多类别0 ,所以一般的选择就是
“牺牲” 类别1,“迁就” 类别0;所以模型的预测结果几乎都为类别0 。
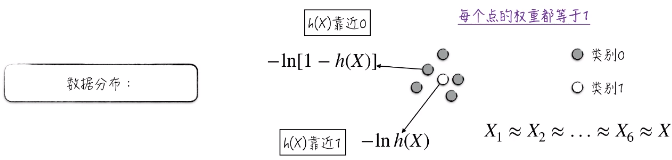
这就导致 h(x) 约等于 0 。

这就是非均衡数据集给建模带来困难的原因。
那么如何解决这个问题呢?我们可以从每个点的权重都等于1 下手。因为权重相同,所以损失函数会牺牲类别1 来满足类别0 的利益。
我们可以调整不同类别的权重。
对于类别0,它的权重变为 -w0 ln[1-h(x)];对于类别1,它的权重变为 -w1 lnh(x) 。这里使 w1 > w0 ,因为我们知道类别1 的个数比较少,所以要调高它的权重。这样调整之后,模型就不会过分满足类别0 的要求。

最后修正逻辑回归的损失函数:

修正过后,模型的效果明显提升。


.jpg) 1. 逻辑回归模型概述。2. 如何评估分类模型的效果。3. 如何解决多元分类问题。4. 非均衡分类问题。
1. 逻辑回归模型概述。2. 如何评估分类模型的效果。3. 如何解决多元分类问题。4. 非均衡分类问题。

