递归
递归需要满足的三个条件
1.一个问题的解可以分解为几个子问题的解
2. 这个问题与分解之后的子问题,除了数据规模不同,求解思路完全一样
3. 存在递归终止条件
假如这里有 n 个台阶,每次你可以跨 1 个台阶或者 2 个台阶,请问走这 n 个台阶有多少种 走法?如果有 7 个台阶,你可以 2,2,2,1 这样子上去,也可以 1,2,1,1,2 这样子 上去,总之走法有很多,那如何用编程求得总共有多少种走法呢? # 所以当 n个台阶的总走法是 是 f(n-1)个走法 + f(n-2)个走法 f(n) =f(n-1) +f(n-2)
因此,编写递归代码的关键是,只要遇到递归,我们就把它抽象成一个递推公式,不用想一 层层的调用关系,不要试图用人脑去分解递归的每个步骤。
递归代码要警惕堆栈溢出
递归代码要警惕重复计算
怎么将递归代码改写为非递归代码?
那是不是所有的递归代码都可以改为这种迭代循环的非递归写法呢?
笼统地讲,是的。因为递归本身就是借助栈来实现的,只不过我们使用的栈是系统或者虚拟 机本身提供的,我们没有感知罢了。如果我们自己在内存堆上实现栈,手动模拟入栈、出栈 过程,这样任何递归代码都可以改写成看上去不是递归代码的样子。
排序
常见排序:插入排序 冒泡排序 选择排序 快排 等等
不常见 : 猴子排序 随眠排序 面条
本节问题
插入 排序和冒泡排序的时间复杂度相同,都是 O(n2), 在实际的软件开发里,为什么我们更倾向于使用插入排序算法而不是冒泡排序算法呢?
如何评价一个排序算法
一.排序时间执行效率
1.最好情况、最坏情况、平均情况时间复杂度
因为有序度的不同会影响 最好最坏平均可能都不相同
2.时间复杂度的系数、常数 、低阶
虽然 两个算法时间复杂度相同 但是对于数据量规模较小的数据来进行比较 那很有可能就无法进行比较 所以要加入这些
3.比较次数和交换(或移动)次数
排序就会涉及这两个操作 所以要考虑
二.排序算法的内存消耗
是否是原地排序 空间复杂度 : O(1)
三.排序算法的稳定性
考虑稳定性 (排序前后 相同对象 位置没有发生变化 那么就是稳定的 比如[1,2,3,3,4,5] 第一个3 和第二个三排序没有变化就是成功的)
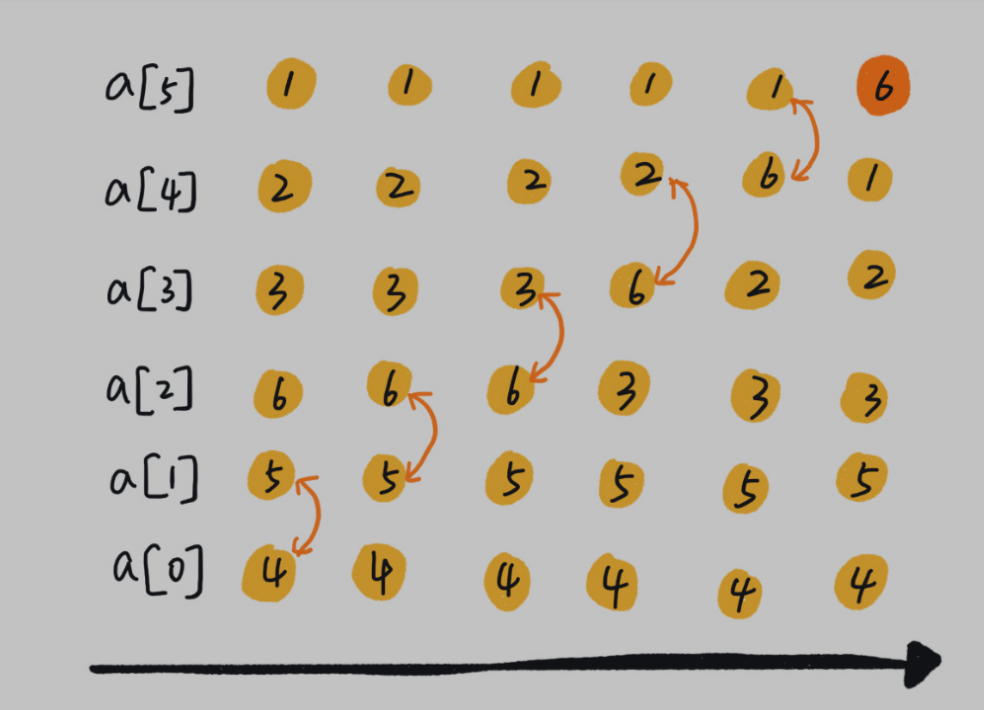
冒泡排序(Bubble Sort)
冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较,看是否
满足大小关系要求。如果不满足就让它俩互换。一次冒泡会让至少
一个元素移动到它应该在的位置,重复 n 次,就完成了 n 个数据的排序工作。

class Maopaofilter():
def __init__(self,l: list):
self.l=l
def __str__(self):
return str(self.l)
def reserver(self,ind):
#ind 与 ind +1 换位置
self.l[ind],self.l[ind+1]=self.l[ind+1],self.l[ind]
def filter(self,reserver=False):
'''
对self.l 进行排序 [4,5,6,7,1,2,3]
#对 所有 元素进行一次便利
:param reserver:
:return:
'''
for i in range(len(self.l)):#次数为n此
for j in range(len(self.l)-i-1):
if self.l[j]>self.l[j+1]:
self.reserver(j)#交换位置函数
l=Maopaofilter([46,4,5,6,2,23,1])
l.filter()
print(l)
回答那三个条件:
1.是原地排序算法
2.是稳定排序
3.冒泡排序的时间复杂度是多少?



