观点1 我们无法孤立数据结构来讲算法,也无法孤立算法来讲数据结构。
我们选择链表这种数据结构,二分查找算法就无法工作了,因为链表并不支持随机访问。
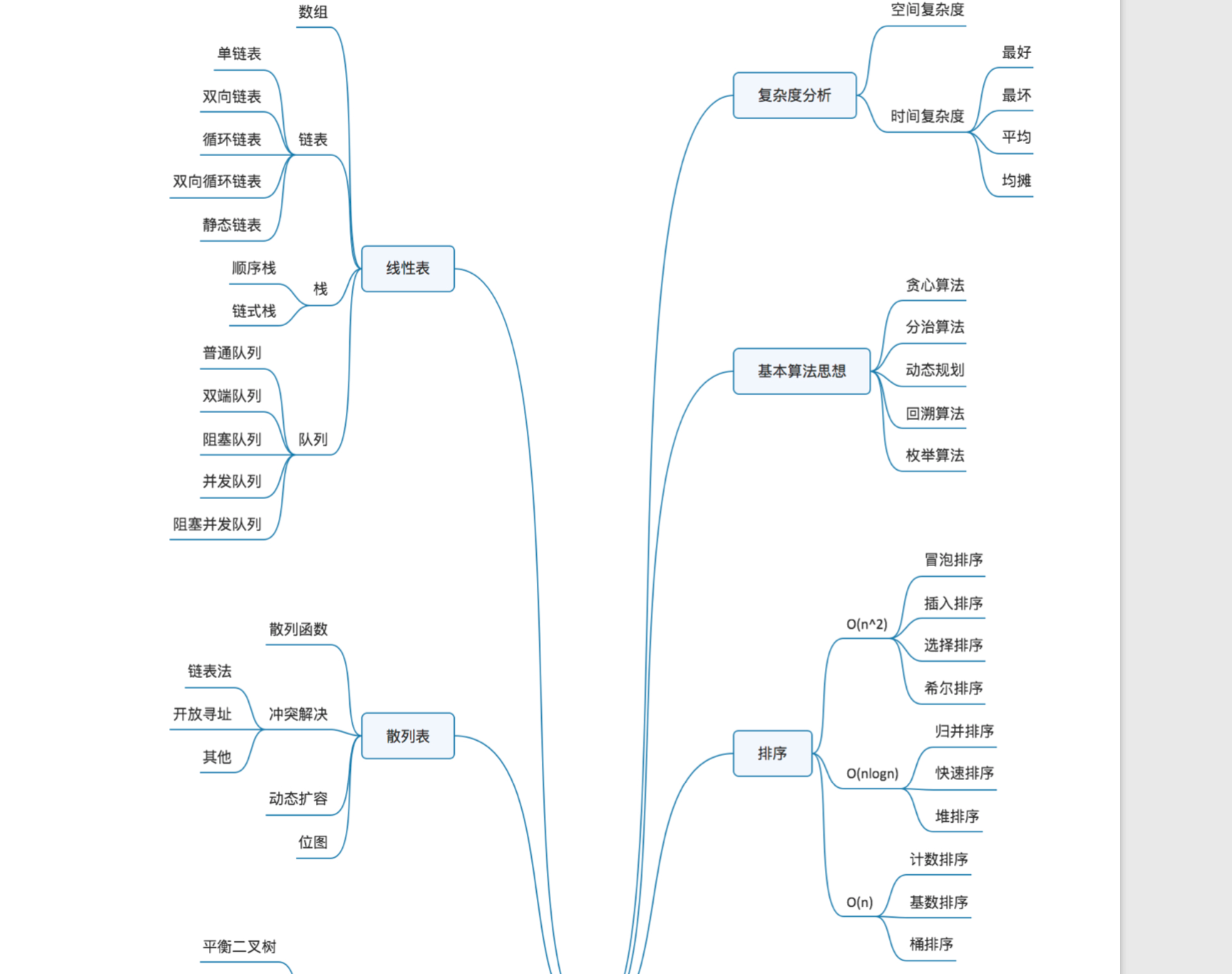
03 | 复杂度分析(上):如何分析、统计算法的执行效率和资源消 耗?


执行时间 (2n+2)*unit_time

所以,整段代码总的执行时间 T(n) = (2n2+2n+3)*unit_time。
而公式中的低阶、常量、系数三部分并 不左右增长趋势,所以都可以忽略
所以只需要记录最大量级就可以了
T(n) = O(n); T(n) = O(n2)。
时间复杂度分析
1. 只关注循环执行次数最多的一段代码
2.加法法则
3. 乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

1.o(1) 和n无关
2.O(logn)、O(nlogn)
i=1 while (i<=n){ i=i*2 }
根据我们前面讲的复杂度分析方法,第三行代码是循环执行次数最多的。所以,我们只要能 计算出这行代码被执行了多少次,就能知道整段代码的时间复杂度。
从代码中可以看出,变量 i 的值从 1 开始取,每循环一次就乘以 2。当大于 n 时,循环结 束。还记得我们高中学过的等比数列吗?实际上,变量 i 的取值就是一个等比数列。如果我 把它一个一个列出来,就应该是这个样子的:
所以,我们只要知道 x 值是多少,就知道这行代码执行的次数了。通过 2x=n 求解 x 这个 问题我们想高中应该就学过了,我就不多说了。x=log2n,所以,这段代码的时间复杂度就 是 O(log2n)。
现在,我把代码稍微改下,你再看看,这段代码的时间复杂度是多少?
根据我刚刚讲的思路,很简单就能看出来,这段代码的时间复杂度为 O(log3n)。
实际上,不管是以 2 为底、以 3 为底,还是以 10 为底,我们可以把所有对数阶的时间复 杂度都记为 O(logn)。为什么呢?
我们知道,对数之间是可以互相转换的,log3n 就等于 log32 * log2n,所以 O(log3n) = O(C * log2n),其中 C=log32 是一个常量。基于我们前面的一个理论:在采用大 O 标记复 杂度的时候,可以忽略系数,即 O(Cf(n)) = O(f(n))。所以,O(log2n) 就等于 O(log3n)。 因此,在对数阶时间复杂度的表示方法里,我们忽略对数的“底”,统一表示为 O(logn)。
如果你理解了我前面讲的 O(logn),那 O(nlogn) 就很容易理解了。还记得我们刚讲的乘法 法则吗?如果一段代码的时间复杂度是 O(logn),我们循环执行 n 遍,时间复杂度就是 O(nlogn) 了。而且,O(nlogn) 也是一种非常常见的算法时间复杂度。比如,归并排序、 快速排序的时间复杂度都是 O(nlogn)。
3. O(m+n)、O(m*n)
基础复杂度分析的知识到此就讲完了,我们来总结一下。
复杂度也叫渐进复杂度,包括时间复杂度和空间复杂度,用来分析算法执行效率与数据规模 之间的增长关系,可以粗略地表示,越高阶复杂度的算法,执行效率越低。常见的复杂度并 不多,从低阶到高阶有:O(1)、O(logn)、O(n)、O(nlogn)、O(n2 )。等你学完整个专栏之 后,你就会发现几乎所有的数据结构和算法的复杂度都跑不出这几个。

5数组为什么从0编号
如何实现随机访问?
1.数组是一种线性表数据结构
2.数组用一组连续的内存空间 存储相同的数据类型
名词1 :线性表
每个只有线性表只有向前向后两个方向 (除了数组是限行结构 还有链表 队列 栈)
非线性并不是简单的前后关系(二叉树 堆 图等)
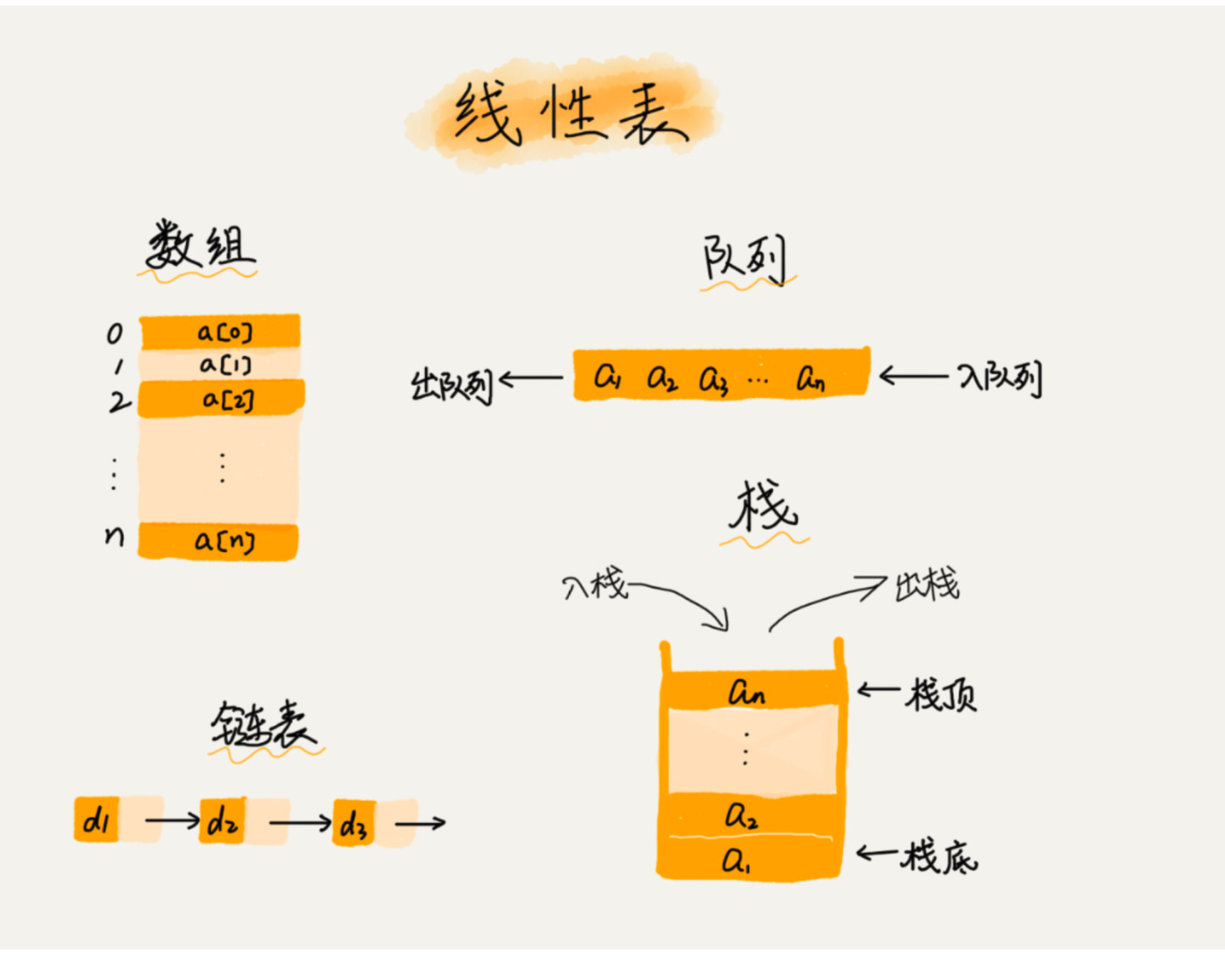

名词2:连续的内存空间和相同类型的数据
利1.具有随机访问
弊1.很多操作低效 (删除或者插入 需要做大量的数据搬移工作)
是怎么记录随机访问的 元素地址=数组baseaddr+元素下标*元素的字节大小 比如 int[1,2,3,4] baseaddr是1000 type_size是8 那么第一个元素 就是1000 第二个元素得知就是1008(1000+8*1)
数组适合查找 不适合插入 琏表适合插入不适合查找
琏表 删除插入是o(1)
数组 查询不是o1 就算排好序用二分也是 o(logn) 根据下标随机访问的时间复杂度才是o(1)
低效的“插入”和“删除”
为什么低效 如何改进
如果数组有顺序:
如果我们需要将一个数据插入到数组中的第 k 个位置。为了 把第 k 个位置腾出来,给新来的数据,我们需要将第 k~n 这部分的元素都顺序地往后挪一 位,时间复杂度就是O(N-K)+O(1) 最终是O(n)
如果数组是无序的
但是,如果数组中存储的数据并没有任何规律,数组只是被当作一个 存储数据的集合。在这种情况下,如果要将某个数组插入到第 k 个位置,为了避免大规模 的数据搬移,我们还有一个简单的办法就是,直接将第 k 位的数据搬移到数组元素的最 后,把新的元素直接放入第 k 个位置。 为了更好地理解,我们举一个例子。假设数组 a[10] 中存储了如下 5 个元素:a,b,c, d,e。 我们现在需要将元素 x 插入到第 3 个位置。我们只需要将 c 放入到 a[5],将 a[2] 赋值为 x 即可。最后,数组中的元素如下: a,b,x,d,e,c。
利用这种处理技巧,在特定场景下,在第 k 个位置插入一个元素的时间复杂度就会降为 O(1)
我们再来看删除操作
我们先把要删除的元素记录 当内存不够用时再执行删除 就不需要一个个删除了 这就提高了删除的效率
警惕数组的访问越界问题

你发现问题了吗?这段代码的运行结果并非是打印三行“hello word”,而是会无限打 印“hello world”,这是为什么呢?
因为,数组大小为 3,a[0],a[1],a[2],而我们的代码因为书写错误,导致 for 循环的结 束条件错写为了 i<=3 而非 i<3,所以当 i=3 时,数组 a[3] 访问越界。
我们知道,在 C 语言中,只要不是访问受限的内存,所有的内存空间都是可以自由访问 的。根据我们前面讲的数组寻址公式,a[3] 也会被定位到某块不属于数组的内存地址上, 而这个地址正好是存储变量 i 的内存地址,那么 a[3]=0 就相当于 i=0,所以就会导致代码 无限循环。
容器能否完全替代数组?
在项目开发中,什么时候适合用数组,什么时候适合用容器呢?
容器可以将很多数据操作封装起来 插入删除时需要搬移其他数据 另一个优势 动态扩容(容器满了 当插入新的值时 分配更大的内存 将数据复制过去 将新的数据插入)
扩容设计耗时(内存申请和搬移) 能确定大小就确定
在高级语言中是不是数组就没用了?
1.java 无法存储基础类型 int long 特别关注性能 或者使用基本类型就选数组
2.数据大小已知 用不到arrlist的方法 数据操作简单 就选数组
3.
06 | 链表(上):如何实现LRU缓存淘汰算法?
缓存满时 哪些数据被淘汰出去 哪些数据应该保留?
1.先进先出策略
2.最少使用
3.最近最少使用
6.1五花八门的链表结构

数组 :如果没有一块连续的内存空间就会申请失败(申请1000m的内存空间 如果没有一块连续的1000m的内存空间 则失败)
链表 :每一个节点存放下一个节点的指针 (指针将内存串联起来)所以非连续的不会有问题
6.1.1 三种常见链表
单向链表 双向链表 循环链表
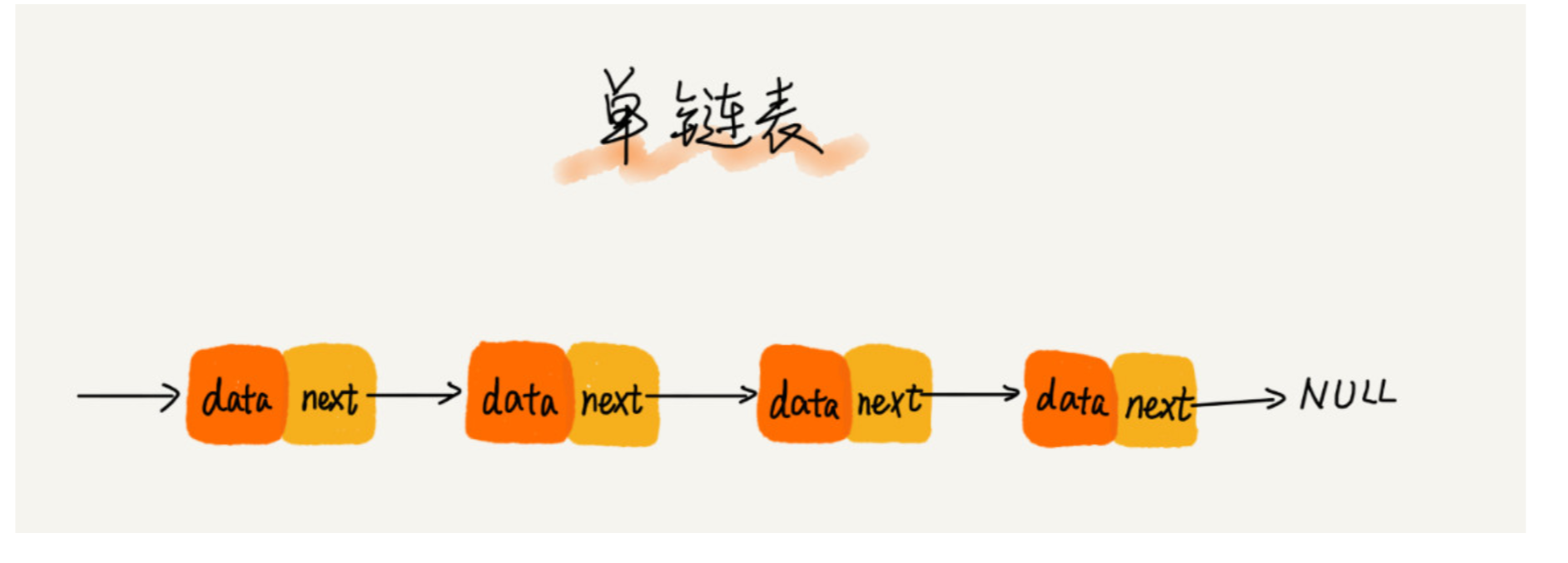
单向链表 : 头节点记录链表的基地址 尾节点指向null
链表 插入删除 时间复杂度o(1)
6.1.2
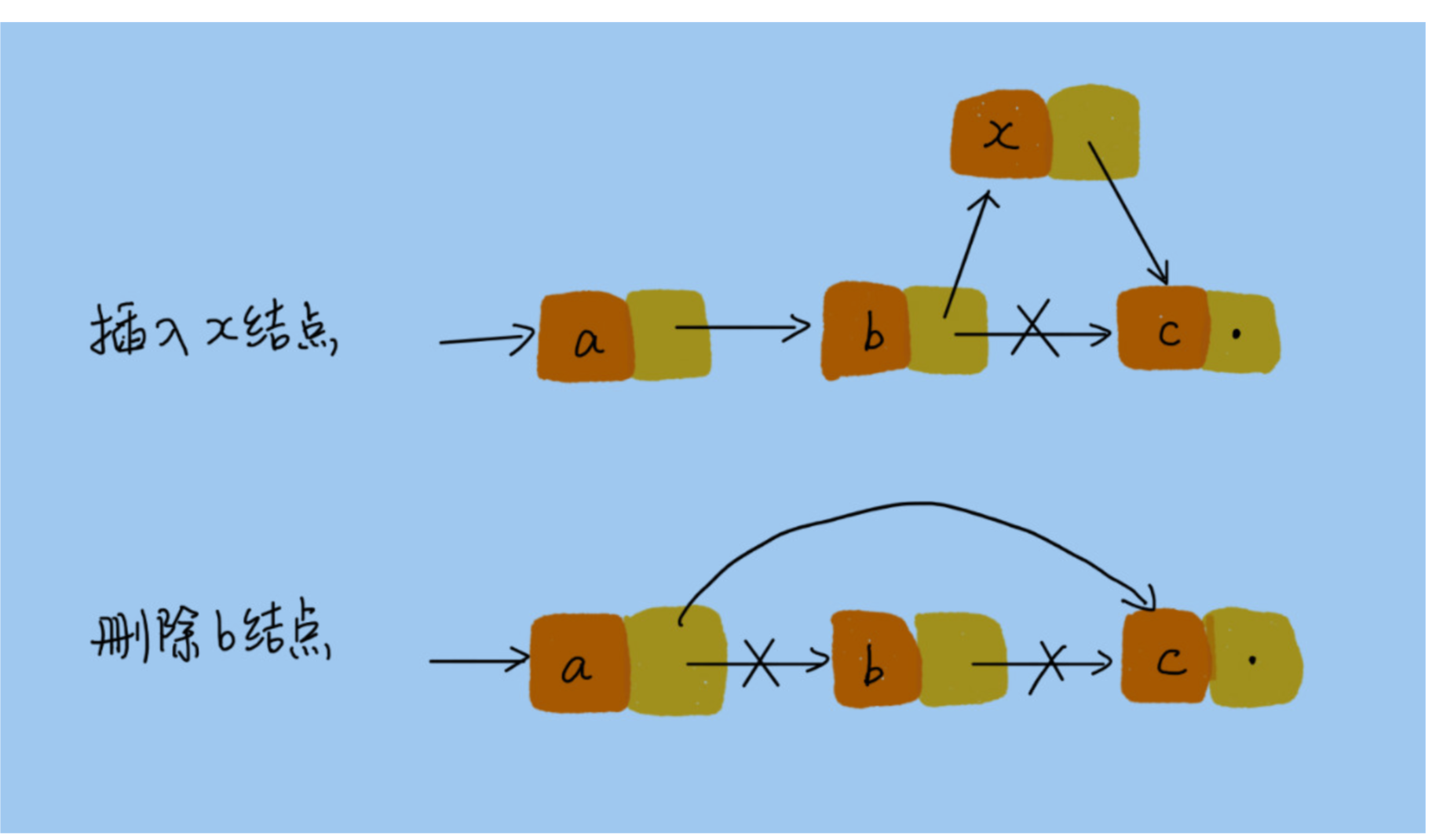
因为只需要改变 上一个节点的指针重新引用就可以了
而因为不是连续的 所以遍历元素需要从头到尾进行遍历 直到找到指定的节点
6.1.3 循环链表
它跟单链表唯一的区别就在尾结点
而循环链表的指针 指向头
6.1.4 双向链表
除了后驱指针 还有一个前驱指针
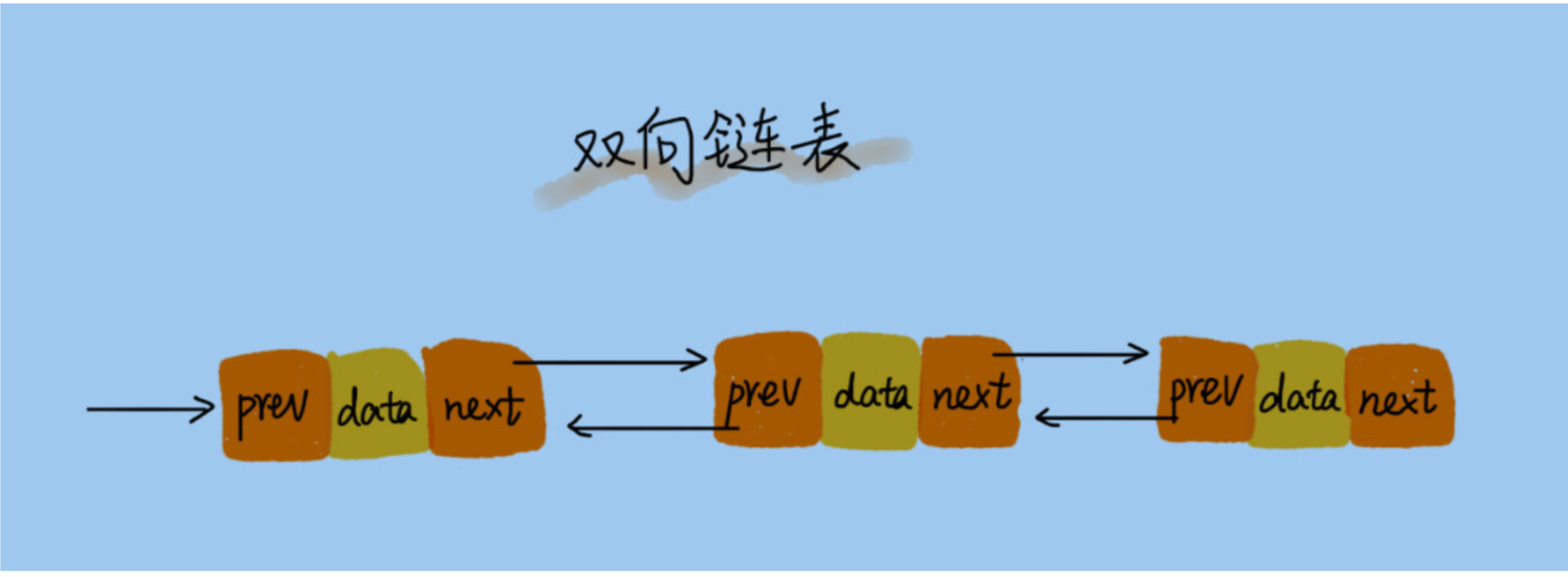
缺点 因为上下指针所以更占内存
优点 支持双向遍历 就因为这样,在某种情况下 插入删除 更高效
删除的操作 删除值 从前往后找到值o(n)找到后 删除o(1) 删除指针对应的节点 单链表 先遍历找到这个节点o(n) 要删除这个节点需要直到前驱节点 所以需要从头遍历 删除o(n-1) 双列表 先遍历找到这个节点o(n) 要删除这个节点需要直到前驱节点 所以需要从头遍历 删除o(1) 插入同理
对于有序的链表来说 查询的效率 双向要大于单向
链表 VS 数组性能大比拼
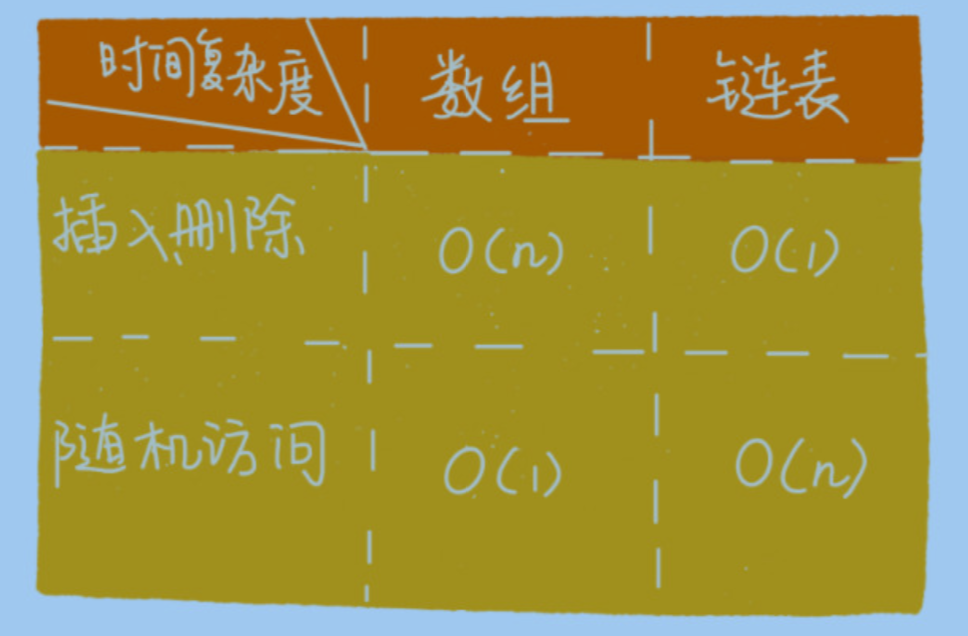
6.2 在实际开发中不能仅仅利用复杂度分析就决定用哪种结构
数组可以使用cpu缓存进行预读(?)
数组缺点是大小固定 申明小了当不够时会申明更大的空间 耗时高 申明大了容易申请失败
链表没有大小限制 天然支持动态扩容
除此之外,如果你的代码对内存的使用非常苛刻,那数组就更适合你。因为链表中的每个结 点都需要消耗额外的存储空间去存储一份指向下一个结点的指针,所以内存消耗会翻倍。而 且,对链表进行频繁的插入、删除操作,还会导致频繁的内存申请和释放,容易造成内存碎 片,如果是 Java 语言,就有可能会导致频繁的 GC(Garbage Collection,垃圾回收)。
6.3如何实现LRU(最近使用缓存策略)缓存策略
维护一个有序列表(最近使用的在链表头部 最早的在链表尾部)
查找元素从前往后
1.如果数据在链表中 那么删除这个节点把他放在开头
2.没有的话分为两种
2.1 缓存未满 将节点直接插入头部
2.2 满了的话 删除最后一个元素 把最新的插入开头
07 | 链表(下):如何轻松写出正确的链表代码?
7.1.几个写链表代码技巧
1.理解指针的概念
2.警惕指针丢失和内存泄漏
3.利用哨兵简化实现难度
#插入一个元素 如果开头是空的那么就把新的数据内存地址当作头节点
#剩下的就是 赋值指针操作
if (head == null) {
head = new_node;
}else{
new_node->next = p->next;
p->next = new_node;
}
答案是哨兵
哨兵解决的是边界问题 不直接参与业务逻辑 如果第一个节点是否为空 头节点都指向哨兵(带哨兵的链表就是带头链表)
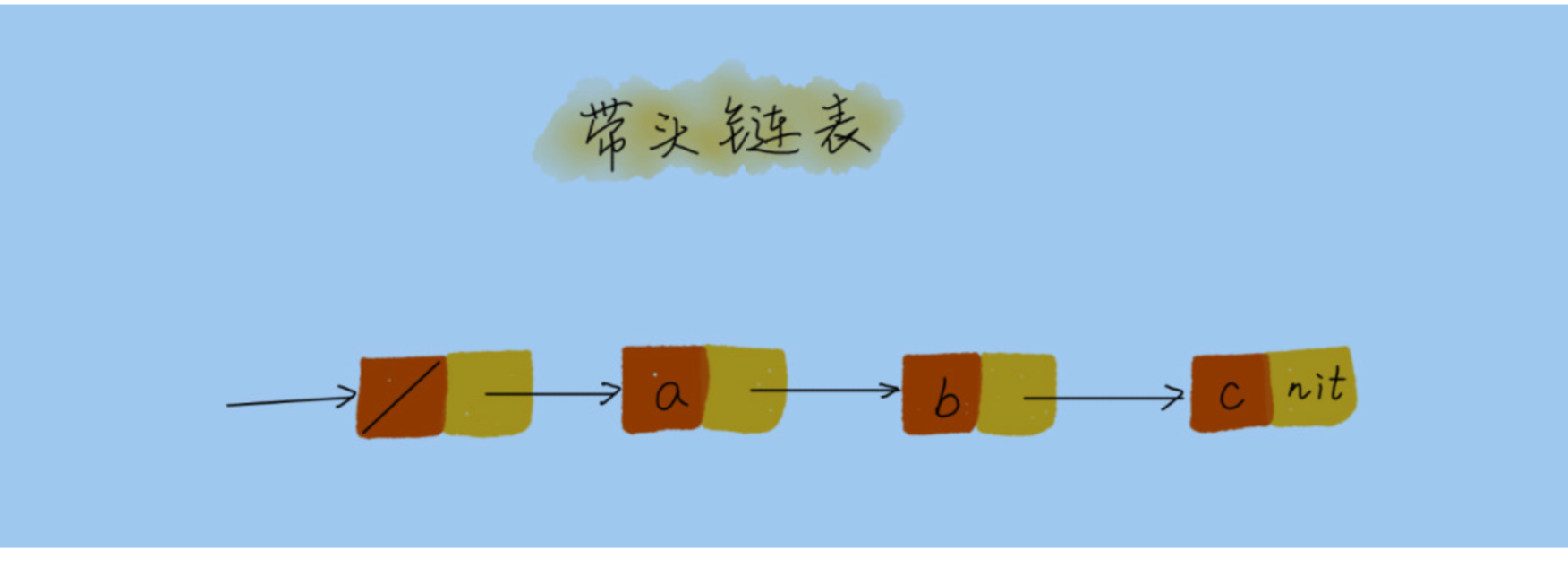
4重点留意边界条件处理
我经常用来检查链表代码是否正确的边界条件有这样几个:
1.链表处理开头和结尾是否遇到问题
2.链表为空是否遇到问题
3.链表只有一个是否会遇到问题
5.举例画图,辅助思考
6:多写多练,没有捷径
单链表反转
链表中环的检测
两个有序的链表合并
删除链表倒数第 n 个结点
求链表的中间结点
08 | 栈:如何实现浏览器的前进和后退功能?
8.1 如何理解“栈”?
后进者先出,先进者后出,这就是典型的“栈”结构(从抽屉里放衣服和拿衣服为例子)
概念1 数组和链表是完全可以代替栈的 但是暴露了太多的接口 使用不可控 自然更容易出错
如果某个数据结构只有先进后出的特性 那么就适合用栈
8.2如何实现一个“栈”?
数组栈:顺序栈
链表栈:链式栈
8.2.1时间空间复杂度是多少呢
为什么不是o(n)呢 因为我们将空间复杂度的时候说过
8.2.2支持动态扩容的顺序栈
我们初始化栈了之后 当栈不够时 就无法添加数据 虽然链式栈没有大小限制 但是要记录下一个节点的指针 还是很耗费空间的 那么我们应该怎么实现一个支持动态扩容的栈呢
当栈满了之后 我们申请一个更大的数组 将原来的数组搬移到新的数组里

8.2.3 入栈和出栈的时间复杂度
出不涉及内存申请 所以复杂度为o1
入栈不一样
当空间不够时 需要申请内存和数据搬移 时间是on
8.2.4 栈在函数调用中的应用
当函数调用时 系统会为每个现成分配内存空间 这种内存空间就像栈 用来存储临时数据变量
每进入函数就会将临时变量 入栈
8.3总结
好了,我想现在你已经完全理解了栈的概念。我们再回来看看开篇的思考题,如何实现浏览
器的前进、后退功能?其实,用两个栈就可以非常完美地解决这个问题。
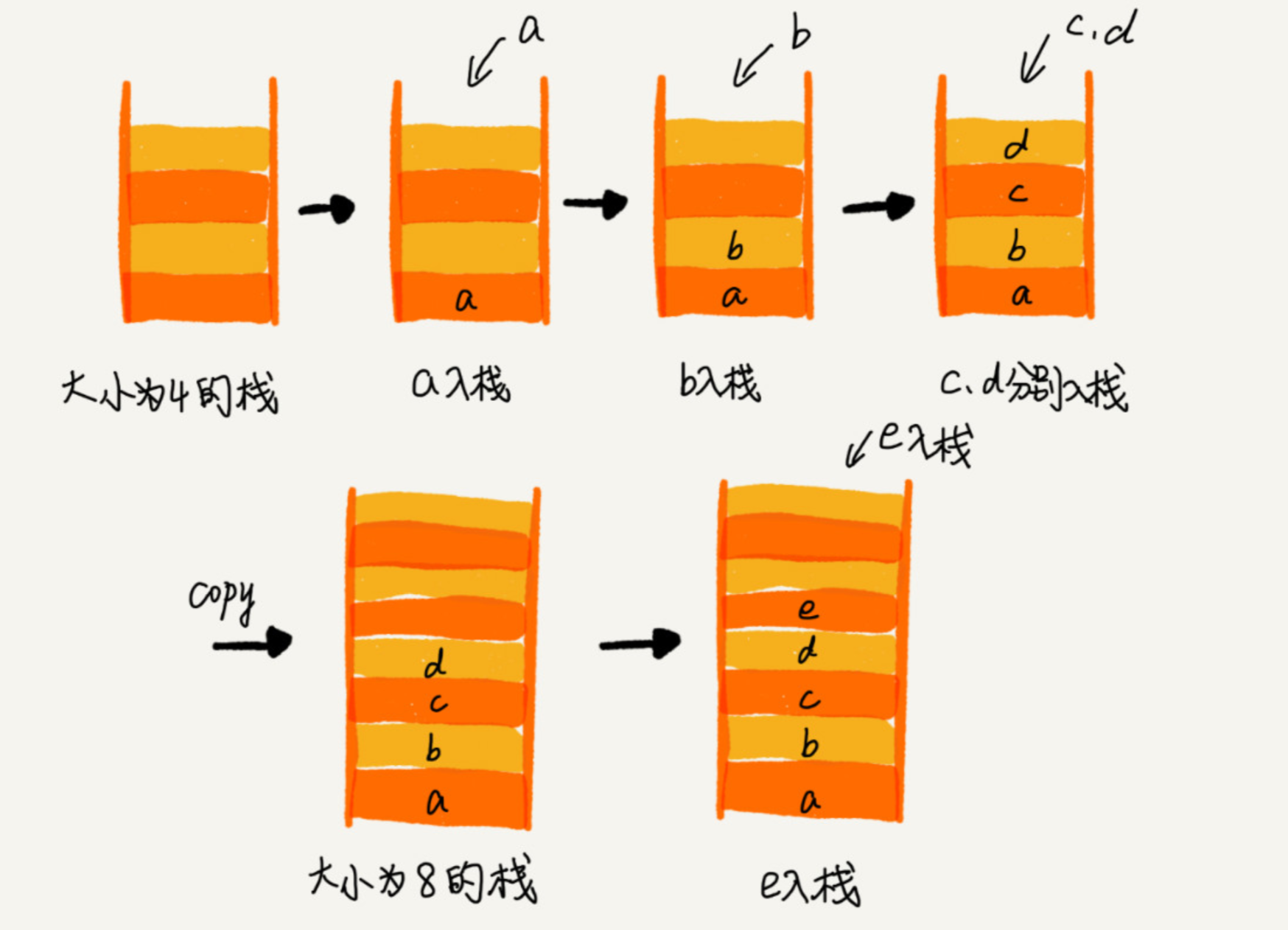
我们使用两个栈,X 和 Y,我们把首次浏览的页面依次压入栈 X,当点击后退按钮时,再依 次从栈 X 中出栈,并将出栈的数据依次放入栈 Y。当我们点击前进按钮时,我们依次从栈 Y 中取出数据,放入栈 X 中。当栈 X 中没有数据时,那就说明没有页面可以继续后退浏览 了。当栈 Y 中没有数据,那就说明没有页面可以点击前进按钮浏览了。
比如你顺序查看了 a,b,c 三个页面,我们就依次把 a,b,c 压入栈,这个时候,两个栈 的数据就是这个样子:
当你通过浏览器的后退按钮,从页面 c 后退到页面 a 之后,我们就依次把 c 和 b 从栈 X 中 弹出,并且依次放入到栈 Y。这个时候,两个栈的数据就是这个样子:
这个时候你又想看页面 b,于是你又点击前进按钮回到 b 页面,我们就把 b 再从栈 Y 中出 栈,放入栈 X 中。此时两个栈的数据是这个样子:
这个时候,你通过页面 b 又跳转到新的页面 d 了,页面 c 就无法再通过前进、后退按钮重 复查看了,所以需要清空栈 Y。此时两个栈的数据这个样子:
09 | 队列:队列在线程池等有限资源池中的应用
9.1如何理解“队列”?
1.排队买票 先来的先买
3.入队 enqueue 出队 dequeue
4 受限操作的线性表结构
6.1.2 具有某些额外特性的队列
循环队列 阻塞队列 并发队列
6.1.3顺序队列和链式队列
同样,用数组实现的队列叫作顺序队列,用链表实现的队列叫作 链式队列。
它具有先进先出的特性,支持在队 尾插入元素,在队头删除元素,那究竟该如何实现一个队列呢?
from typing import Optional
class ArrayQueue:
def __init__(self, capacity: int):
self._items = []
self._capacity = capacity
self._head = 0
self._tail = 0
def enqueue(self, item: str) -> bool:
if self._tail == self._capacity:
if self._head == 0:
return False
else:
for i in range(0, self._tail - self._head):
self._items[i] = self._items[i + self._head]
self._tail = self._tail - self._head
self._head = 0
self._items.insert(self._tail, item)
self._tail += 1
return True
def dequeue(self) -> Optional[str]:
if self._head != self._tail:
item = self._items[self._head]
self._head += 1
return item
else:
return None
def __repr__(self) -> str:
return " ".join(item for item in self._items[self._head : self._tail])
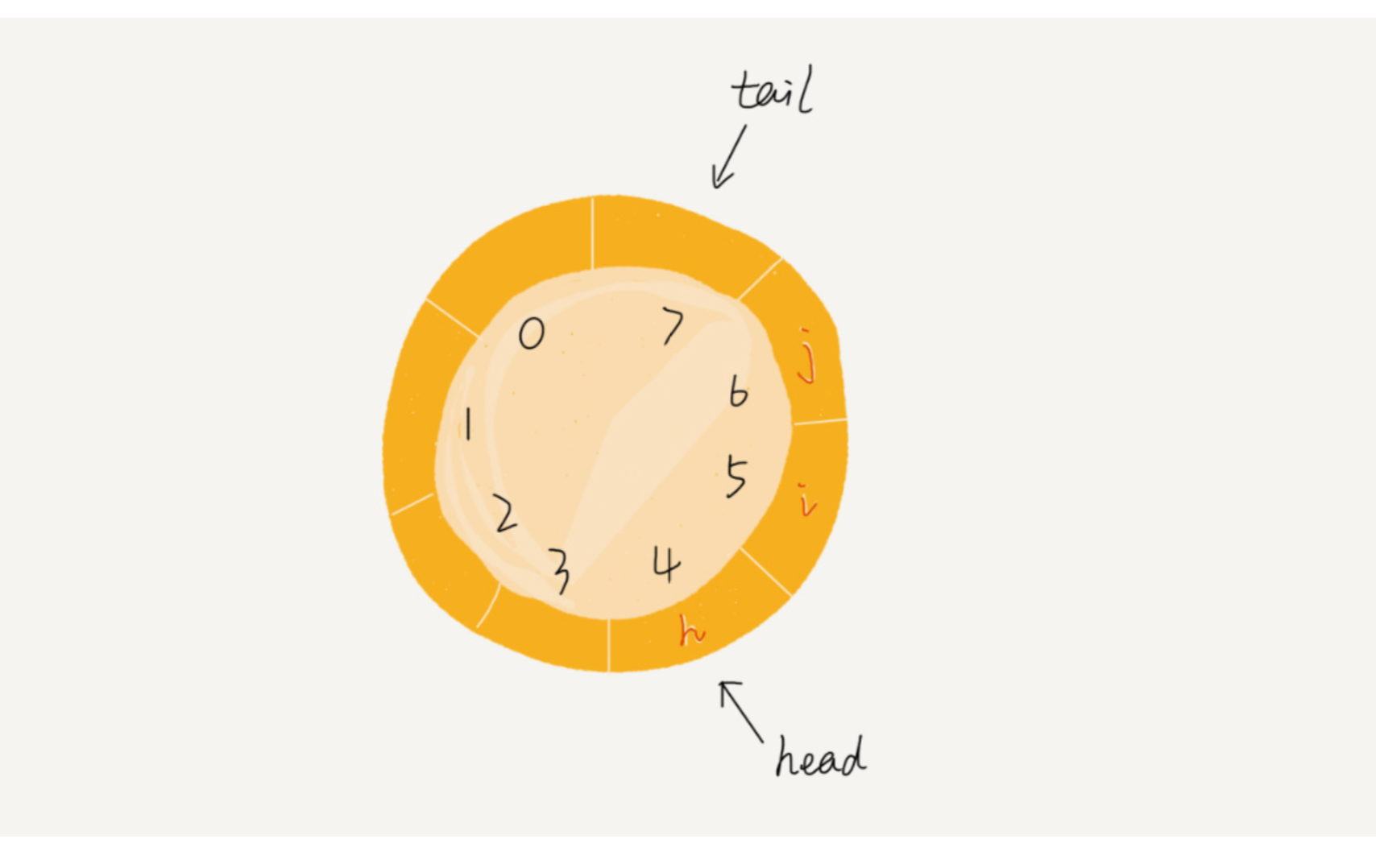
6.1.4队列需要两个指针:一个是 head 指 针,指向队头;一个是 tail 指针,指向队尾。
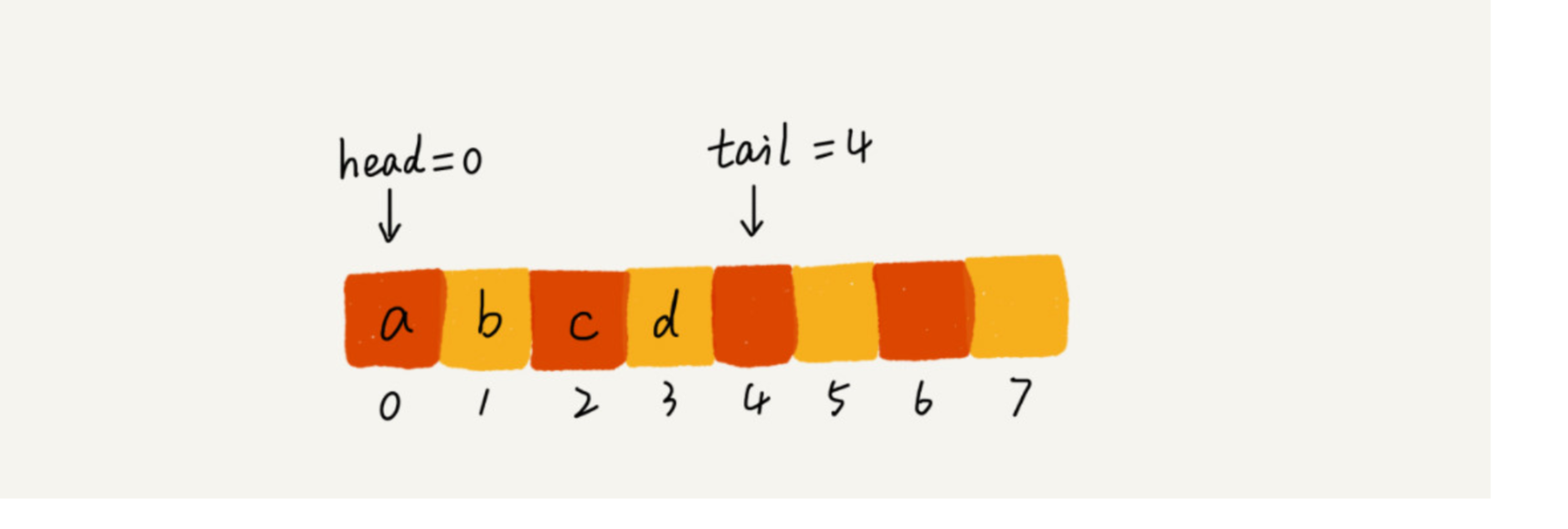
当我们调用两次出队操作之后,队列中 head 指针指向下标为 2 的位置,tail 指针仍然指向 下标为 4 的位置。
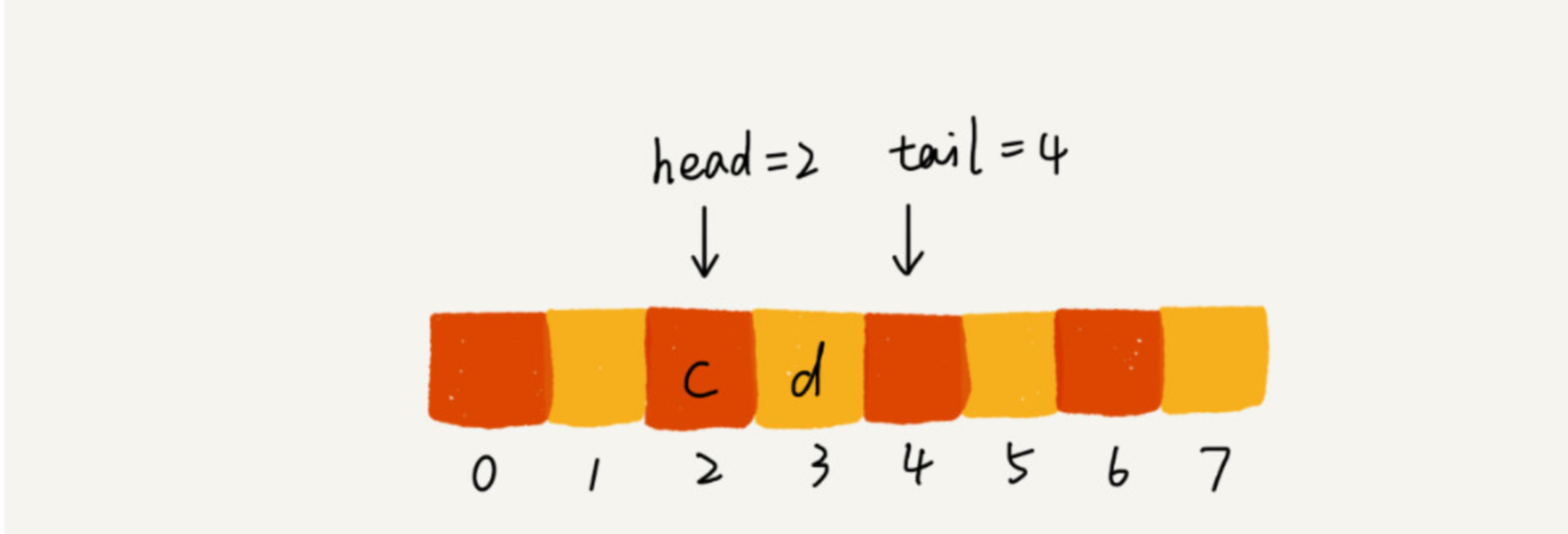
你肯定已经发现了,随着不停地进行入队、出队操作,head 和 tail 都会持续往后移动。
6.2.1当 tail 移动到最右边,即使数组中还有空闲空间,也无法继续往队列中添加数据了。这个问题 该如何解决呢?
用数据搬移 (出队删除下标为0的位置 要数据搬移那么时间复杂度就是 on)
实际上,我们在出队时可以不用搬移数据
当数组满了 入队时集中处理搬移操作 所以我们改变入队操作就可以了
from typing import Optional
class DynamicArrayQueue:
def __init__(self, capacity: int):
self._items = []
self._capacity = capacity
self._head = 0
self._tail = 0
def enqueue(self, item: str) -> bool:
if self._tail == self._capacity:
if self._head == 0: return False
self._items[0 : self._tail - self._head] = self._items[self._head : self._tail]
self._tail -= self._head
self._head = 0
if self._tail == len(self._items):
self._items.append(item)
else:
self._items[self._tail] = item
self._tail += 1
return True
def dequeue(self) -> Optional[str]:
if self._head != self._tail:
item = self._items[self._head]
self._head += 1
return item
def __repr__(self) -> str:
return " ".join(item for item in self._items[self._head:self._tail])
if __name__ == "__main__":
q = DynamicArrayQueue(10)
for i in range(10):
q.enqueue(str(i))
print(q)
for _ in range(3):
q.dequeue()
print(q)
q.enqueue("7")
q.enqueue("8")
这样入队出队的操作 都是o1
6.3接下来,我们再来看下基于链表的队列实现方法。
入队时,tail->next= new_node, tail = tail- >next;出队时,head = head->next。
#尾部指针指向新的节点 #指针还在原来位置上那么 tail 指向新的节点
from typing import Optional
class DynamicArrayQueue:
def __init__(self, capacity: int):
self._items = []
self._capacity = capacity
self._head = 0
self._tail = 0
def enqueue(self, item: str) -> bool:
if self._tail == self._capacity:
if self._head == 0: return False
self._items[0 : self._tail - self._head] = self._items[self._head : self._tail]
self._tail -= self._head
self._head = 0
if self._tail == len(self._items):
self._items.append(item)
else:
self._items[self._tail] = item
self._tail += 1
return True
def dequeue(self) -> Optional[str]:
if self._head != self._tail:
item = self._items[self._head]
self._head += 1
return item
def __repr__(self) -> str:
return " ".join(item for item in self._items[self._head:self._tail])
if __name__ == "__main__":
q = DynamicArrayQueue(10)
for i in range(10):
q.enqueue(str(i))
print(q)
for _ in range(3):
q.dequeue()
print(q)
q.enqueue("7")
q.enqueue("8")
print(q)

6.4 循环队列
当插入 ab时
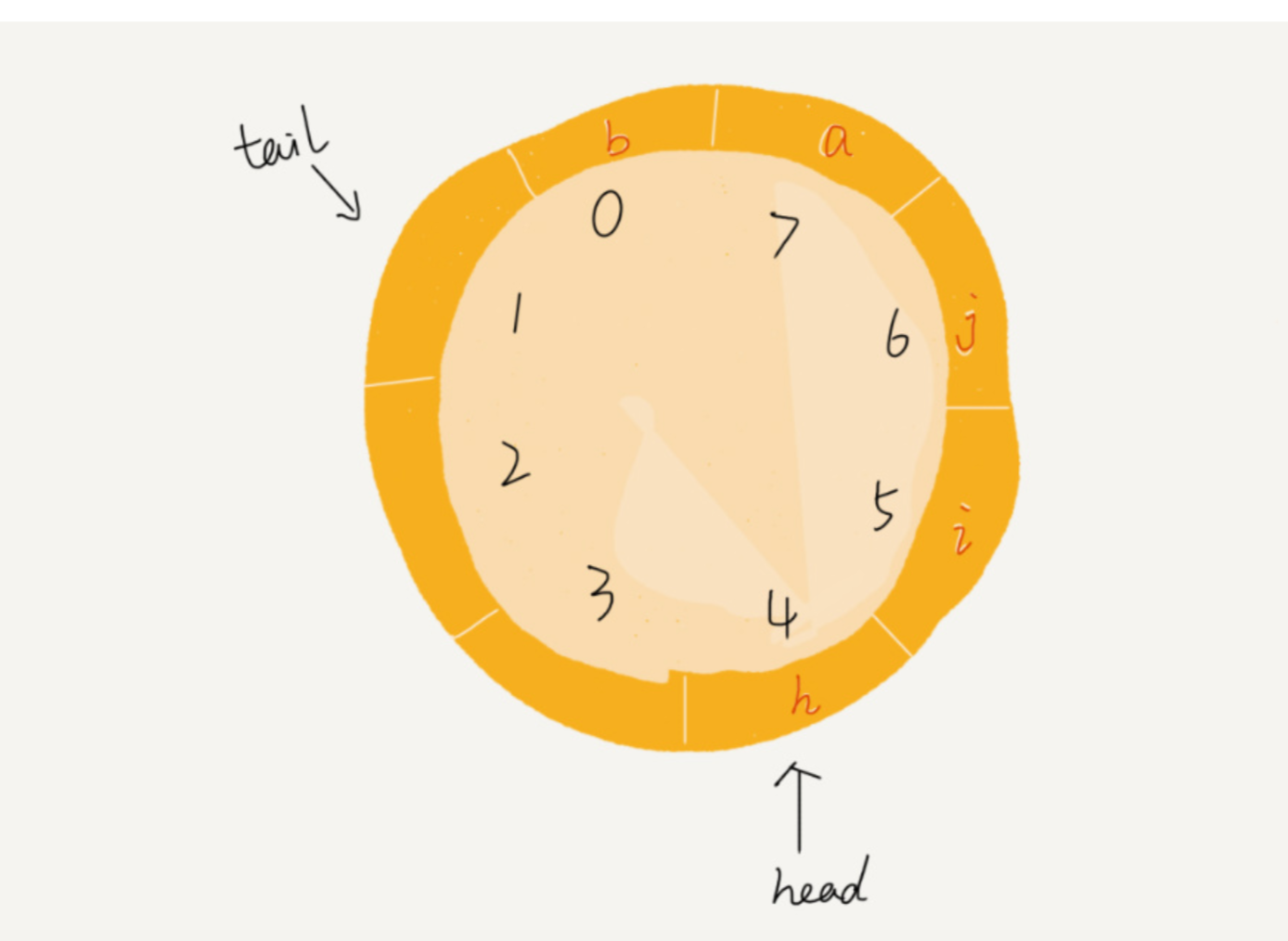
在写的过程中一定要
确定好队空和队满的判定条件
from typing import Optional
from itertools import chain
class CircularQueue:
def __init__(self, capacity):
self._items = []
self._capacity = capacity + 1
self._head = 0
self._tail = 0
def enqueue(self, item: str) -> bool:
# 传递一个字符串
# 如果尾部索引+1 就是头索引的话 就无法操作 (当索引是最后的时候 索引+1=0 ) 【预判一下 当头索引和尾索引碰在一起时 就无法入队操作了】
if (self._tail + 1) % self._capacity == self._head:
return False
# 队列里加入这个数组
self._items.append(item)
#当索引溢出时 归0
self._tail = (self._tail + 1) % self._capacity
return True
def dequeue(self) -> Optional[str]:
#头索引等于尾索引时 不允许出队操作
if self._head != self._tail:
# 返回头指针往后移动一个位置
item = self._items[self._head]
#头指针+1 如果溢出了就+1
self._head = (self._head + 1) % self._capacity
return item
def __repr__(self) -> str:
if self._tail >= self._head:
return " ".join(item for item in self._items[self._head: self._tail])
else:
return " ".join(item for item in chain(self._items[self._head:], self._items[:self._tail]))
if __name__ == "__main__":
q = CircularQueue(5)
for i in range(5):
q.enqueue(str(i))
q.dequeue()
q.dequeue()
print(q)
6.5阻塞队列和并发队列
阻塞对列 当队列数据为空或者为满时 取数据和查数据的操作结果不会立马返回 而是会阻塞 直到插入一个数据和取出一个数据
并发队列 当多线程操作同一份数据时 会设计线程安全 如何实现线程安全队列呢
最简单直接的实现方式是直接在 enqueue()、 dequeue() 方法上加锁,但是锁粒度大并发度会比较低 (
基于数组的循环队列,利用 CAS 原子操作,可以实现非常高效的并发队列
)
6.6解答开篇
处理方式有两种
1.非阻塞 直接返回结果 要么none 要么数据
2.阻塞 请求排队
6.2.1队列中 链表和数组 两种实现对于排队请求有什么区别呢
链表 因为是具有无界的 所以会导致过多的请求排队 请求的时间会很长 所以响应时间久 (对于响应时间比较敏感的系统 不太适合)
数组 队列太大导致等待请求过多 队列太小无法充分利用计算机优势
除了前面讲到队列应用在线程池请求排队的场景之外,队列可以应用在任何有限资源池中, 用于排队请求,比如数据库连接池等。实际上,对于大部分资源有限的场景,当没有空闲资 源时,基本上都可以通过“队列”这种数据结构来实现请求排队。