数论攻克
引子
前天打了南京站的网络赛,南航杀我,有一道叫super_log的题,题目要求算出幂塔函数共 b 个 a 乘幂的结果模 m 的值。
虽然我当时不会手码快速幂,但是板子还是有的,于是我把取模的快速幂放上去,递归快速幂一串后发现(妈妈我递归没错了!),最后一个样例算出的是126。
不对,可能是因为我的指数取模了所以结果不对了,于是我直属放弃了递归,在最后就快速幂取模一次,样例通过了。
开心,提交,不出所料,TLE。
之后就对1900ms优化到1000ms束手无策了🙈。
于是我看了题解,题解大人是这么写的:
由于指数会很大,使用欧拉定理递归降幂即可。需要特判一下a与m不互质的情况。 欧拉函数很快会迭代到1,可以提前退出,速度很快。
我这才发现原来我做不出的原来以前都学过,哭了,数论嘛,我重新学好了吧,欧拉方程和欧拉定理、欧拉公式不同好了好了我知道了,那么我们开始吧!
OPEN
第一步我们从ppt开始吧(对不起师哥我一定学会!)
1. 自然数分为质数和合数,对于质数的判断:
Code

bool is_prime(int n){ if(n == 2 || n == 3) return true; if(n % 6 != 1 && n % 6 != 5) return false; for(int i = 5; i < (int)sqrt(n)+1;i+=6){ if(n % i == 0 || n % (i+2) == 0) return false; } return true; }
2. 因子分解定理
对于任意一个正整数,一定可以被唯一分解为若干个质数的乘积的形式:
n = p1a1 × p2a2 × ... × pkak
其中,pi 是n的质因子,ai 是pi 的个数。
因子分解过程:从2到sqrt(n)枚举因子 k ,判断n是否可以被k整除。在整个过程中,每找到n的因子,将n /= k,
使对应的枚举上限因此变小。因此对于合数复杂度<O(sqrt(n)),而质数最坏为O(sqrt(n)),可以通过预先打好质数表,如果n为质数则跳出。
Code
(普通正整数的因子分解)(此代码不包含质数表)(返回的num值为存储质因子的真实大小)

1 const int maxn = 1e5 + 10; 2 int cnt[maxn]; 3 int fac[maxn]; 4 int getFac(int n) 5 { 6 int num = 0, sum = 0, m = sqrt(n + 0.5); 7 for (int k = 2; k <= m; k++) 8 { 9 sum = 0; 10 while (n % k == 0) 11 { 12 n /= k; 13 sum++; 14 } 15 if (sum != 0) 16 { 17 fac[num] = k; 18 cnt[num++] = sum; 19 } 20 m = sqrt(n + 0.5); 21 } 22 if (n != 1) 23 { 24 fac[num] = n; 25 cnt[num++] = 1; 26 } 27 return num; 28 }
因子个数D:正整数n的所有不同因子的总个数,计算公式:
D = (a1+1) × (a2+1) × ... × (ak+1)
证明:组合数学的方法
因子求和S:正整数n的所有不同因子的总和,计算公式:
S = Π[ 1 + pi + pi2 + … + piai ] = Π[ (pi(ai+1) - 1)/(pi-1) ]
证明:多项式乘法的展开式
Example
12的因子有1、2、3、4、6、12,总计6个,因子和S=1+2+3+4+6+12=28
分解质因子得到12=22 x 31,代入公式因子个数D=(2+1)x(1+1)=6,所有因子和S=(1+2+4) x (1+3) = 28
阶乘的因子分解:给定正整数n,分别求n! 的因子分解式中质因子pi 的数量ai ,计算公式:
SF(p) = ∑[ n/(pk) ] = n/p + n/(p2) + n/(p3) + … + n/(pk)
其中pk <=n,时间复杂度为O(log(n)),只需要枚举质因子,然后分别按照上述方式分解即可
-》洛谷P2043:当时没看到这里,直接求出阶乘后再用(Code:getFactor)去求,结果97! 比long long还长直接爆了,还是入门题,哭了orz
Code
Ⅰ:for i in range(1, n), getFactor(i), cnt[i] += sum;(抛弃了num[]数组,i表示所存质因子)为入门标解

1 #pragma warning (disable:4996) 2 #include <algorithm> 3 #include <iostream> 4 #include <iomanip> 5 #include <string> 6 #include <cstdio> 7 #include <cmath> 8 #define MS(x) memset(x,0,sizeof(x)) 9 using namespace std; 10 typedef long long ll; 11 12 const int maxn = 1e5 + 10; 13 int cnt[maxn] = { 0 }; 14 15 int main() 16 { 17 int n; 18 scanf("%d", &n); 19 for (int i = 1; i <= n; i++) 20 { 21 int m = sqrt(i + 0.5), i2 = i; 22 for (int k = 2; k <= m; k++) 23 { 24 while (i2 % k == 0) 25 { 26 i2 /= k; 27 cnt[k]++; 28 } 29 m = sqrt(i2 + 0.5); 30 } 31 if (i2 != 1) 32 cnt[i2] += 1; 33 } 34 for (int i = 1; i <= n; i++) 35 { 36 if (cnt[i] != 0) 37 printf("%d %d\n", i, cnt[i]); 38 } 39 return 0; 40 }
Ⅱ:线性筛素数n,再对于n内所有的素数分别代入公式SF(P),推荐程度满星!但事实是可能由于测试数据过小筛素数还慢些🙈
(线性筛素数详见后文)

1 #pragma warning (disable:4996) 2 #include <algorithm> 3 #include <iostream> 4 #include <iomanip> 5 #include <cstring> 6 #include <string> 7 #include <cstdio> 8 #include <queue> 9 #include <stack> 10 #include <cmath> 11 #include <map> 12 #include <set> 13 #define MS(x) memset(x,0,sizeof(x)) 14 using namespace std; 15 typedef long long ll; 16 const int maxn = 1e6 + 10; 17 18 int prime[maxn], cnt[maxn] = { 0 }; 19 bool check[maxn]; 20 21 int getp(int n) 22 { 23 int num = 0; 24 MS(check); 25 for (int i = 2; i <= n; i++) 26 { 27 if (!check[i]) 28 prime[++num] = i; 29 for (int j = 1; j <= num; j++) 30 { 31 if (i * prime[j] > n) 32 break; 33 check[i * prime[j]] = 1; 34 if (i % prime[j] == 0) 35 break; 36 } 37 } 38 return num; 39 } 40 41 int main() 42 { 43 int n; 44 scanf("%d", &n); 45 int num = getp(n); 46 for (int i = 1; i <= n; i++) 47 { 48 int i2 = i; 49 for (int j = 1; j <= num; j++) 50 { 51 while (i2 % prime[j] == 0) 52 { 53 i2 /= prime[j]; 54 cnt[j]++; 55 } 56 } 57 } 58 for (int i = 1; i <= num; i++) 59 { 60 if (cnt[i] != 0) 61 printf("%d %d\n", prime[i], cnt[i]); 62 } 63 return 0; 64 }
应用:求n!的末尾有多少个零
思路:考虑求n!的因子分解式中有多少个2和5
3. 最大公因数 && 最小公倍数
首先歪果仁的辗转相除法确实在大的数据面前比我们自家的什么更像减损术要快得多,原理:
gcd(a, b) = gcd(a, a%b);
Code
仅限求两个数之间的gcd
Ⅰ:循环求gcd

int gcd(int a, int b) { if (b == 0) return a; int r = a % b; while (r != 0) { a = b; b = r; r = a % b; } return b; }
Ⅱ:递归求gcd

int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); }
Quality
1.结合律) GCD(a,b,c)=GCD(GCD(a,b), c)
2.区间) GCD( al , … , ar )=GCD(GCD( al , … , am-1 ), GCD(am , … , ar ))
3.分配律) GCD(k*a, k*b)=k × GCD(a, b)
4.互质) 若GCD(a, b)=p,则a/p与b/p互质
5.线性变换) GCD(a+k*b, b)=GCD(a, b)
6.因子分解) GCD(a, b)=Π[ pimin(ai,bi) ]
根据最大公因数我们很容易就可以得到其最小公倍数
lcm(a, b) = (a*b) / gcd(a, b)
(上述计算容易溢出,且仅限求两个数之间的lcm)
Quality
1.结合律) LCM(a, b, c)=LCM(LCM(a, b), c)
2.分配律) LCM(k*a, k*b)=k*LCM(a, b)
3.因子分解) LCM(a, b)=Π[ pimax(ai, bi) ]
4. 欧拉函数
欧拉函数Φ(n)表示所有小于正整数n并与n互质的正整数的个数,计算公式:
Φ(n) = n × ∏[ 1 - 1/pi ]
Example
Φ(12) = 22-1 x 31-1 x (2-1) x (3-1) = 2 x 1 x 1 x 2 = 4
说明在比12小的所有正整数当中,共有4个数与12互质,这4个数分别是1、5、7、11
Quality
1) 对任意正奇数n,Φ(n)=φ(2*n),特别规定Φ(1)=1
2) 对任意质数n,Φ(n)=n-1,Φ(nk) = (n-1) * nk-1 (此处即可联系引理②)=nk - nk-1=nk * (1 - 1/n) = nk * ((n - 1)/n)
3) 若a, b互质,则有Φ(a * b) = Φ( a ) * φ( b ) (积性函数)
证明:
1.容斥原理证明
2.欧拉函数的积性性质
-------------------------------------------
根据2)、3)两个性质再结合n的质因子分解即可有:
Code
求正整数n的欧拉函数-->O(sqrt(n))

1 int euler(int n) 2 { 3 /* 4 根据因子分解定理设 n = a^2 * b * c; a,b,c为质数a^2, b, c一定互质(害臊就别问我为什么) 5 又根据Ⅰ若a,b互质,则有Φ(a * b) = φ( a ) * φ( b )Ⅱ若p为质数,则φ(p^k) = p^k - p^(k-1) = p^k * (1 - 1/p) = p^k * ((p - 1)/p) 6 φ(n) = φ(a^2 * b * c) = φ(a^2) * φ(b) * φ(c) = a^2 * ((a-1)/a) * b * ((b-1)/b) * c * ((c-1)/c) 7 = a^2 * b * c * ((a-1)/a) * ((b-1)/b) * ((c-1)/c) = n * ((a-1)/a) * ((b-1)/b) * ((c-1)/c) 8 故用for循环和while循环在sqrt(n)的时间上来找出a,b,c即可 9 */ 10 int ret = n; 11 12 for (int i = 2; i <= sqrt(n + 0.5); i++) 13 { 14 if (n % i == 0) 15 { 16 ret = ret / i * (i - 1);//先进行除法防止溢出——>ret = ret * (1 - 1 / p(i)) 17 while (n % i == 0) 18 n /= i; 19 } 20 } 21 if (n > 1) 22 ret = ret / n * (n - 1); 23 return ret; 24 }
欧拉线性筛求素数-->O(n)(比经典埃氏筛法的O(n*loglongn)在较大数据时更快)

1 const int maxn = 1e7 + 10, maxp = 1e6 + 10; 2 int prime[maxp + 10], num = 0; 3 bool check[maxn + 10]; 4 void FetPhi() 5 { 6 MS(check); 7 for (int i = 2; i < maxn; i++) 8 { 9 if (check[i] == 0) 10 prime[num++] = i; 11 for (int j = 0; j < num; j++) 12 { 13 if (i * prime[j] > maxn) 14 break; 15 check[i * prime[j]] = 1; 16 if (i % prime[j] == 0) 17 break; 18 } 19 } 20 }
大名鼎鼎的线性晒日常筛素数的速度大概是埃氏筛的3-4倍,然而在小数据中却有被完爆的可能QAQ
所以欧拉筛法不只是拿来筛个素数,更重要的一点是线性筛可以用来求解积性函数【完全积性函数f(x)应满足对于任意的a与b,当a与b互质时,f(a×b)=f(a)×f(b)】
根据2)、3)性质,我们可以得到如下引理👇(亲证有效)

欧拉函数的线性筛-->O(n)(在线性筛素数的同时筛出欧拉函数,增加了一个phi[]数组)

1 const int maxn = 1e7 + 10, maxp = 1e6 + 10; 2 int prime[maxp + 10], phi[maxn + 10], num = 0; 3 bool check[maxn + 10]; 4 void FetPhi() 5 { 6 phi[1] = 1; 7 MS(check); 8 for (int i = 2; i < maxn; i++) 9 { 10 if (check[i] == 0) 11 prime[num++] = i, phi[i] = i - 1;//① 12 for (int j = 0; j < num; j++) 13 { 14 if (i * prime[j] > maxn) 15 break; 16 check[i * prime[j]] = 1; 17 if (i % prime[j] == 0) 18 { 19 phi[i * prime[j]] = phi[i] * prime[j];//② 20 break; 21 } 22 else 23 phi[i * prime[j]] = phi[i] * (prime[j] - 1);//③ 24 } 25 } 26 }
(不根据线性筛素数的板子拓展的话,我们还可以少用一个check[]获得更短的代码)

1 void Eulerfilter() 2 phi[1] = 1; 3 for (int i = 2; i <= maxn; ++i) 4 { 5 if (!phi[i])pri[++tot] = i, phi[i] = i - 1;//由于check[]下标和phi变化一致 6 for (int j = 1; j <= tot; ++j) 7 { 8 if (i * pri[j] > maxn)break; 9 if (!(i % pri[j])) 10 { 11 phi[i * pri[j]] = phi[i] * pri[j]; 12 break; 13 } 14 else 15 phi[i * pri[j]] = phi[i] * (pri[j] - 1); 16 } 17 } 18 }
对于线性筛的几点解释:
1.细节打表
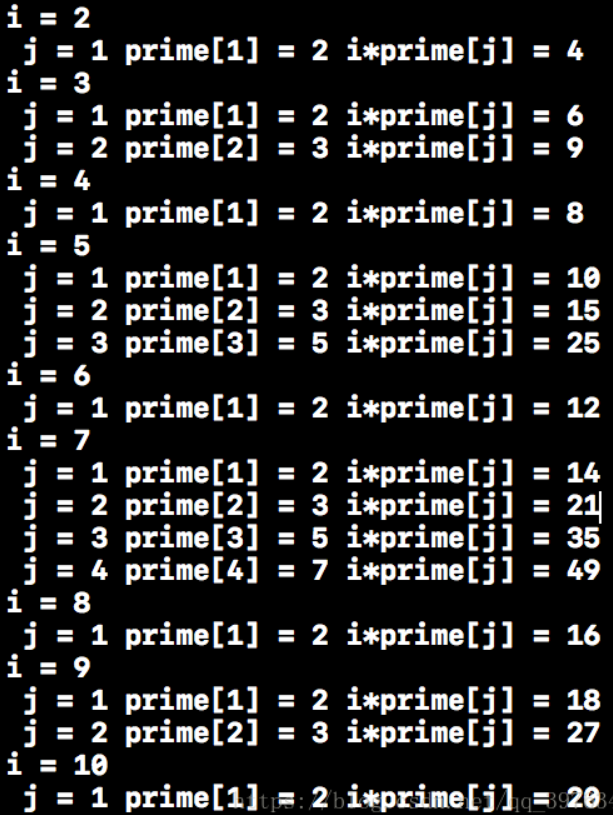
2. 关于灵魂代码[ if( i % prime[j] == 0) break; ] :当 i是prime[j]的倍数时,i = kprime[j],如果继续运算 j+1,i * prime[j+1] = prime[j] * k prime[j+1],这里prime[j]是最小的素因子,当i = k * prime[j+1]时会重复,所以才跳出循环例如i = 8 ,j = 1,prime[j] = 2,如果不跳出循环,prime[j+1] = 3,8 * 3 = 2 * 4 * 3 = 2 * 12,在i = 12时会计算。因为欧拉筛法的原理便是只最小素因子来消除素数,从而比埃氏筛法少重复许多重复筛除的操作。
5. 模运算
Quality
1) (a + b) % p=(a%p + b%p) % p
2) (a - b) % p=(a%p - b%p + p) % p
3) (a * b) % p=((a%p) * (b%p)) % p
4) (a / b) % p=((a%p) * inv(b)) % p,其中inv(b)表示b%p的逆元
大整数取模:对一个非常大的正整数n(比如1000位数),和一个非常小的正整数p(在int范围以内),求n%p,可以将大整数n改写成 Σ[ ai x 10i ] 的形式,这样求 Σ[ ai x 10i ] % p 就等价于Σ[ ( (ai%p) x (10i %p) %p ] %p
Example
12345可以改写为1x104+2x103+3x102+4x10+5的形式,然后使用模运算的性质即可
Ⅰ. 快速幂:
【O(log(n))】-->将n转换成二进制形式,通过“&1”取二进制末位判断奇偶(x&1==0为偶,x&1==1为奇)和“>>”右移去掉最后一位
Example
a11=a(2^0+2^1+2^3) ,11的二进制是1011,11 = 2³×1 + 2²×0 + 2¹×1 + 2º×1,因此,我们将a¹¹转化为算 a2^0 × a2^1 × a2^3,也就是a1 × a2 × a8 ,相比于pow()的11次乘法,我们的思路是通过3次相乘就得到结果。对于1011,每次判断 if (b&1 != 0)来确定是否参与ans(2base × 1 or 0)的运算,从base = a对应a2^0 开始不断让base累乘使base值依次达到a2^1, a2^2 = a4 ,a2^3 = a8 以便在(b&1 != 0)时贡献ans的乘值。
Code

1 ll qpow(int a, int b) {//求x在%mod意义下的逆元 2 int base = a; ll ans = 1; 3 while (b) { 4 if (b & 1)ans = base * ans % MOD; 5 base = base * base % MOD; b >>= 1; 6 }return ans; 7 }
Ⅱ. 逆元:
逆元:若(a×b) % p=1,即(a×b) ≡ 1(mod p),则 b 是正整数 a 在模 p 下的逆元 (0<x<p)
根据模运算公式,在需要计算a/b mod p的结果时,只要计算a×b' mod p的结果即可,其中 b' 为 b在mod p下的逆元,相当于倒数的存在
Quality
1)唯一性:对于任意实数a,有且只有一个逆元a'
2)完全积性:设a=inv[a],则inv[a] * inv[b] = inv[a*b]
求正整数a在模mod下逆元的方法主要有👇
(单个)法一:费马小定理
【要求a与mod互质,快速幂优化,时间复杂度O(log(n))】
费马小定理:若存在一质数p,且对于任意整数a有a和p互质,则有 a(p-1) % p = 1,即 a(p-1) ≡ 1(mod p)
Example
3和5互质,那么3(5-1) % 5=34 % 5= 81%5 = 1
由 a(p-1) % p = (a x a(p-2)) % p = 1,联系逆元性质 (a×b) % p=1
或 a(p-1) ≡ 1(mod p) --> a × a(p-2) ≡ 1(mod p), 联系逆元性质 (a×b) ≡ 1(mod p) 可得:
inv[a] = a(p-2) % p -->(a(p-2) 需要快速幂优化)
Code

1 inline ll Fermat(int x) {//求x在%mod意义下的逆元 2 int y = MOD - 2; ll res = 1; 3 while (y) { 4 if (y & 1)res = res * x % MOD; 5 x = x * x % MOD; y >>= 1; 6 }return res; 7 }
inline ll Fermat(int a) { return qpow(a, MOD - 2); }
(单个)法二:拓展欧几里德
【只要求a与mod互质,时间复杂度O(log(n))】【用来应对费马小定理快速幂面对毒瘤题longlong模数溢出的状况】
拓展欧几里德定理:对于不完全为0的非负整数a和b,必定存在整数对(x1, y1),使等式 x1 × a + y1 × b = gcd(a, b) 成立----①
同理,存在整数对(x2, y2),使等式 x2 × b + y2 × (a % b) = gcd(b, a%b) 成立----②

void Euclid() { gcd(a, b) == gcd(b, a % b); x2 × b + y2 × (a % b) == x1 × a + y1 × b; //因为a % b = a - (a / b * b), 你要是觉得 a/b*b == a 就去复读吧 x2 × b + y2 × (a - (a / b * b)) == x1 × a + y1 × b; y2 × a + (x2 - y2 × a / b) × b == x1 × a + y1 × b; //整合a,b前缀式 x1 == y2,y1 = x2 - y2 × a / b; }
由此可根据x1 = y2,y1 = (x2 - y2 × a / b)来求出 x1,y1
当a,b互质(gcd(a, b) = 1)时,原方程化为x1 × a + y1 × b = 1
等同于--> x1 × a ≡ 1(mod b) 或 y1 × b ≡ 1(mod a),联系 a × b ≡ 1(mod p)知 x1,y1分别为a,b的逆元
而对于x1,y1,我们可以根据上述推导过程进行递归求解(这个递归的ans与x,y无关)(居然误导我好几天想不明白气死🙈)
exgcd(a,b,x,y)求的是a对于mod b下的逆元x以及b对于mod a下的逆元y
Code

1 int exgcd(int a, int b, int& x, int& y) 2 { 3 if (b == 0) { 4 x = 1; 5 y = 0; 6 return a; 7 } 8 int ans = exgcd(b, a % b, y, x); 9 y -= a / b * x; 10 return ans; //这个ans一直代表的就是gcd(a,b)的值(亏我纠结了好几天怎么ans不变不是逆元值(/^\)) 11 }
其他应用👇
① 求解ax + by = c,c为任意整数
推导:设ax + by = gcd(a, b)有特解(x'0, y'0)(这个解由拓展欧几里得算法求出),在等式两边同乘 c/gcd(a, b)【c/gcd(a, b)必须为整数,否则没有整数解】
得 a * x'0 * (c/gcd(a, b)) + b * y'0 * (c/gcd(a, b)) = c,故(x'0 * c/gcd(a, b))与 (y'0 * c/gcd(a, b))便为 ax + by = c 的一组整数解 ( 本身整数解即有无数个 ( 包括负数解 ) )
设 x0 = x'0 * c/gcd(a, b),y0 = y'0 * c/gcd(a, b),对于ax + by = c 则有通解:
x' = x0 + b/gcd(a, b) * k
y' = y0 + a/gcd(a, b) * k ----->(k为任意整数)
Code
② 求线性同余方程 a * x ≡ b(mod n) 的最小正整数解
将方程改写为 a * x - n * y = b 的形式,根据①求出一组特解(x0, y0)
令k = n / gcd(a, n),则 xmin 可通过该表达式求出:
x = (x0 % k + k) % k
Code
(批量)法三:线性递推打表 (同余定理)
【只要求mod是质数,时间复杂度O(n)】
同余定理:给定一个正整数mod,如果两个整数a和b满足(a-b)%m=0,那么就称整数a与b对模m同余,记作a ≡ b(mod m)
也可以理解为a与b对n取模后得到的余数相等,即a%n=b%n
Quality
同余式相加:若a≡b(mod m),c ≡ d(mod m),则a±c ≡ b±d(mod m)
同余式相乘:若a≡b(mod m),c ≡ d(mod m),则a×c ≡ b×d(mod m)
Code ( inv[i] = (mod - mod / i) * inv[mod % i] % mod )

void getinv() { int i, mod = 1e9 + 7; int a = mod / i, b = mod % i; mod = a * i + b; a * i + b ≡ 0 % mod; -a * i ≡ b % mod; //同余定理的线性运算性质 //因为b * inv[b] ≡ 1 % mod,i * inv[i] ≡ 1 % mod,根据同余式相乘约去i,b转化为其逆元inv[]最后化简得 -a * inv[b] ≡ inv[i] % mod; //将a,b代回得到仅对于i与mod的关系式 -mod / i * inv[mod % i] ≡ inv[i] % mod; //同余定理的交换性 inv[i] ≡ -mod / i * inv[mod % i] % mod; //因为 mod * inv[mod % i] ≡ 0 % mod;根据同余式相加 inv[i] ≡ (mod - mod / i) * inv[mod % i] % mod; }

1 const ll mod = 1e9 + 7; 2 ll inv[maxn]; 3 void getInv(int n) 4 { 5 inv[1] = 1; 6 for (ll i = 2; i <= n; i++) 7 inv[i] = (mod - mod / i) * inv[mod % i] % mod; 8 return; 9 }
(单个)法四:欧拉定理
【只要求a与mod互质,需要欧拉函数与快速幂】
欧拉定理:若a和p互质,则 aφ(p) % p =1,即aφ(p) ≡ 1(mod p),inv[a] = (aφ(p)-1) % p
特别地,当p为质数时,φ(p) = p-1,上式转化为费马小定理,所以欧拉函数是费马小定理的推广形式
拓展欧拉定理
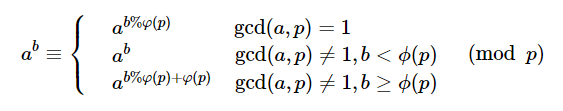
根据拓展欧拉定理(以后有脑子的时候再去看看别人的证明吧,现在咱会用就行= =)
因此对于求 ab(mod n),我们可以直接转换为上式中的一个。
由此得到技能:欧拉降幂👉 洛谷P4139
Code

1 #pragma warning (disable:4996) 2 #include <algorithm> 3 #include <iostream> 4 #include <iomanip> 5 #include <cstring> 6 #include <string> 7 #include <cstdio> 8 #include <stack> 9 #include <cmath> 10 #define MS(x) memset(x,0,sizeof(x)) 11 using namespace std; 12 typedef long long ll; 13 typedef unsigned long long ull; 14 const int maxn = 1e7 + 5; 15 using namespace std; 16 17 int phi[maxn], pri[maxn]; 18 19 void FetPhi() 20 { 21 ll num = 0; 22 phi[1] = 1; 23 for (int i = 2; i < maxn; i++) 24 { 25 if (phi[i] == 0) 26 pri[++num] = i, phi[i] = i - 1; 27 for (int j = 1; j <= num; j++) 28 { 29 if (i * pri[j] > maxn) 30 break; 31 if (i % pri[j] == 0) 32 { 33 phi[i * pri[j]] = phi[i] * pri[j]; 34 break; 35 } 36 else 37 phi[i * pri[j]] = phi[i] * (pri[j] - 1); 38 } 39 } 40 } 41 42 ll qpow(ll x, ll y, ll mod) 43 { 44 ll ret = 1; 45 while (y) 46 { 47 if (y & 1)ret = ret * x % mod; 48 x = x * x % mod, y >>= 1; 49 } 50 return ret; 51 } 52 ll Solve(ll mod) 53 { 54 if (mod == 1)return 0; //phi[1] = 0,你懂的 55 return qpow(2, Solve(phi[mod]) + phi[mod], mod);//原式 = 2^((剩余数 % phi[mod]) + phi[mod]) 56 //而(剩余数 % phi[mod])又可以分解递归,与原式相比只是模数变成了phi[mod]而已 57 } 58 59 int main() 60 { 61 FetPhi(); 62 int T; 63 scanf("%d", &T); 64 while (T--) 65 { 66 int p; 67 scanf("%d", &p); 68 printf("%lld\n", Solve(p)); 69 } 70 return 0; 71 }
》还不快回到顶部看看你那道没做出来的super_log!!
Code

#pragma warning (disable:4996) #include <algorithm> #include <iostream> #include <iomanip> #include <cstring> #include <string> #include <cstdio> #include <stack> #include <cmath> #define MS(x) memset(x,0,sizeof(x)) using namespace std; typedef long long ll; typedef unsigned long long ull; const int maxn = 1e7 + 5; using namespace std; int phi[maxn], pri[maxn]; void FetPhi()//一个平淡无奇的欧拉线性筛 { ll num = 0; phi[1] = 1; for (int i = 2; i < maxn; i++) { if (phi[i] == 0) pri[++num] = i, phi[i] = i - 1; for (int j = 1; j <= num; j++) { if (i * pri[j] > maxn) break; if (i % pri[j] == 0) { phi[i * pri[j]] = phi[i] * pri[j]; break; } else phi[i * pri[j]] = phi[i] * (pri[j] - 1); } } } ll qpow(ll x, ll y, ll mod)//一个平淡无奇的快速幂 { ll ret = 1; while (y) { if (y & 1) ret = ret * x % mod; x = x * x % mod; y >>= 1; } return ret; } ll Solve(ll mod, int base, int t)//一个通过拓欧计算幂塔函数的神奇递归函数 { if (mod == 1)return 0;//任何数对1取模皆为0 if (t == 0)return 1;//幂塔级数到顶 ll solve = Solve(phi[mod], base, t - 1); //return qpow(base, Solve(phi[mod], base, t - 1) + phi[mod], mod);//必WA无疑!!! //我们需要判断(b = Solve(phi[mod], base, t - 1))是否>= phi[mod] if (solve < phi[mod] && solve) return qpow(base, solve, mod); return qpow(base, solve + phi[mod], mod); } int main() { FetPhi(); int T; scanf("%d", &T); while (T--) { int a, b, m; scanf("%d %d %d", &a, &b, &m); printf("%d\n", Solve(m, a, b)); } return 0; }
//这里某些题解又说不用考虑gcd(a, p),emmm后面那个判断retrun再想想吧,这个博客代码的心路历程应该和我差不多hh......
后来发现很多类似算法是有一个Mod()函数,关于Mod的相关说明见此博客了解
感觉Mod还是正规一点的算法,以后用这个吧🙈(两种方法可以对比一下)

1 /* 2 要点: 3 4 1.快速幂和cal函数都要换成Mod; 5 2.最终答案需要模p 6 */ 7 #pragma warning (disable:4996) 8 #include <algorithm> 9 #include <iostream> 10 #include <iomanip> 11 #include <cstring> 12 #include <string> 13 #include <cstdio> 14 #include <stack> 15 #include <cmath> 16 #define MS(x) memset(x,0,sizeof(x)) 17 #define Mod(a,b) a<b?a:a%b+b//只需重写 Mod 函数,就能当作 a 与 b 互素处理 18 using namespace std; 19 typedef long long ll; 20 typedef unsigned long long ull; 21 const int maxn = 1e7 + 5; 22 using namespace std; 23 24 int phi[maxn], pri[maxn]; 25 26 void FetPhi()//一个平淡无奇的欧拉线性筛 27 { 28 ll num = 0; 29 phi[1] = 1; 30 for (int i = 2; i < maxn; i++) 31 { 32 if (phi[i] == 0) 33 pri[++num] = i, phi[i] = i - 1; 34 for (int j = 1; j <= num; j++) 35 { 36 if (i * pri[j] > maxn) 37 break; 38 if (i % pri[j] == 0) 39 { 40 phi[i * pri[j]] = phi[i] * pri[j]; 41 break; 42 } 43 else 44 phi[i * pri[j]] = phi[i] * (pri[j] - 1); 45 } 46 } 47 } 48 49 ll qpow(ll x, ll y, ll mod)//一个不那么平淡无奇的改装快速幂 50 { 51 ll ret = 1; 52 while (y) 53 { 54 if (y & 1) 55 ret = Mod(ret * x, mod); 56 x = Mod(x * x, mod); 57 y >>= 1; 58 } 59 return ret; 60 } 61 62 ll Solve(ll a, ll b, ll mod)//一个由于Mod()重构从而可以无视不互质情况的递归求幂塔函数 63 { 64 if (mod == 1)return Mod(a, mod);//任何数对1取模皆为0,但是和没有Mod()不同,这里不会再在原Solve里加上phi[mod],所以直接返回当前数字 65 if (b == 0)return 1;//幂塔级数到顶 66 return qpow(a, Solve(a, b - 1, phi[mod]), mod);//万物皆互质 67 } 68 int main() 69 { 70 FetPhi(); 71 int T; 72 scanf("%d", &T); 73 while (T--) 74 { 75 ll a, b, m; 76 scanf("%lld %lld %lld", &a, &b, &m); 77 printf("%lld\n", Solve(a, b, m) % m); 78 } 79 return 0; 80 }
CodeForces906D :与super_log、上帝与集合的正确用法差不多,感觉AC无敌乐2233

1 #pragma warning (disable:4996) 2 #include <algorithm> 3 #include <iostream> 4 #include <vector> 5 #include <iomanip> 6 #include <cstring> 7 #include <string> 8 #include <cstdio> 9 #include <map> 10 #include <stack> 11 #include <cmath> 12 #define MS(x) memset(x,0,sizeof(x)) 13 #define Mod(a,b) a<b?a:a%b+b//只需重写 Mod 函数,就能当作 a 与 b 互素处理 14 using namespace std; 15 typedef long long ll; 16 typedef unsigned long long ull; 17 const int maxn = 1e8 + 5; 18 using namespace std; 19 20 int sequence[100050]; 21 map<ll, ll> phi; 22 23 ll euler(ll n)//由于mod最高有1e9,数组没有那么大,于是我们只能放弃欧拉线性筛单个求它 24 //这个时候要加个map记忆化一下(虽然死活不想) 25 { 26 int ret = n; 27 if (phi[ret]) 28 return phi[ret];//记忆化 29 for (int i = 2; i <= sqrt(n + 0.5); i++) 30 { 31 if (n % i == 0) 32 { 33 ret = ret / i * (i - 1); 34 while (n % i == 0) 35 { 36 n /= i; 37 } 38 } 39 } 40 if (n > 1) 41 ret = ret / n * (n - 1); 42 phi[n] = ret;//记忆化 43 return ret; 44 } 45 46 ll qpow(ll x, ll y, ll mod)//一个不那么平淡无奇的改装快速幂 47 { 48 ll ret = 1; 49 while (y) 50 { 51 if (y & 1) 52 ret = Mod(ret * x, mod); 53 x = Mod(x * x, mod); 54 y >>= 1; 55 } 56 return ret; 57 } 58 59 ll Solve(ll a, ll b, ll mod)//一个由于Mod()重构从而可以无视不互质情况的递归求幂塔函数 60 { 61 if (mod == 1 || b == a)return Mod(sequence[a], mod);//任何数对1取模皆为0,但是和没有Mod()不同,这里不会再在原Solve里加上phi[mod],所以直接返回当前数字 62 //幂塔级数到顶 63 return qpow(sequence[a], Solve(a + 1, b, euler(mod)), mod);//万物皆互质 64 } 65 int main() 66 { 67 int len, m, s; 68 scanf("%d %d", &len, &m); 69 for (int i = 1; i <= len; i++) 70 scanf("%d", &sequence[i]); 71 int qn; 72 scanf("%d", &qn); 73 ll l, r, ans; 74 while (qn--) 75 { 76 scanf("%lld %lld", &l, &r); 77 ans = Solve(l, r, m) % m; 78 printf("%lld\n", ans); 79 } 80 return 0; 81 }
6. 中国剩余定理
中国剩余定理:设正整数N满足线性同余方程组 N ≡ ai (mod pi ),其中 1<=i<=n,pi 两两互质(特别注意),则有
N = Σ[ ai * Wi * inv(Wi , pi) ] % M
其中,M = Πpi = p1 * p2 * … * pn,Wi = M / pi,inv(Wi , pi) 表示Wi在模pi下的逆元
毫无疑问公式十分复杂,让我们看看著名的孙子问题:
Example
今有物不知其数,三三数之剩二(除以3余2),五五数之剩三(除以5余3),七七数之剩二(除以7余2),问物几何?
————《孙子算经》
Solve
① 找出三个数:在7和5的公倍数中找出除3余1的最小数70、3和7的公倍数中找出除5余1的最小数21、5和3的公倍数中找出除7余1的最小数15
② 将70乘2(2为Answer除以3的余数)、21乘3(3为Answer除以5的余数)、15乘2(2为Answer除以7的余数)的积相加得到15∗2+21∗3+70∗2=233
③ 将233除以3、5、7三个数的最小公倍数105,得233%105=23,此余数23即为符合条件的最小数
Code
Ⅰ. 模数两两互质(拓展欧几里得求逆元)
Ⅱ. 模数两两不互质

