算法与数据结构(一)
学习慕课网《算法与数据结构》
目录:
第一节:简介
第二节、排序基础
1.冒泡排序
2.选择排序
3.插入排序
4.希尔排序
第三节、高级排序算法
1.归并排序
2.快速排序
思考题
第四节、堆和堆排序
1.最大堆
1)最大堆添加元素
2)最大堆中取出元素
3)最大堆排序
4)原地堆排序
5)最大索引堆
2.最小堆
排序算法总结
思考题
第五节、二分搜索树
1.二分查找法
2.二叉搜索树
1)二叉搜索树插入元素
2)二叉搜索树查找元素
3)二叉搜索树遍历元素
4)二叉搜索树删除节点
第一节、简介
学了那么多算法与数据结构,最后用慕课网的实战《算法与数据结构来做一次总结》
有需要这门视频的同学可以留言邮箱我会将百度云链接发给他
测试1:普通随机数组
测试2:接近有序的数组
测试3:大量重复数据的数组
我的简单测试案例:[ 5, 8, 3, 6, 4, 2, 1, 7]
第二节、排序基础
1.冒泡排序
冒泡排序(Bubble Sort),是一种计算机科学领域的较简单的排序算法。
它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。
这个算法的名字由来是因为越大的元素会经由交换慢慢“浮”到数列的顶端,故名“冒泡排序”。
1)普通版冒泡排序(与后一个位置元素比较,若较小,当前位置与后一个位置进行交换)
2)改进版冒泡排序(保存当前位置的值,与后一个位置元素比较,若较小,后一个位置的值赋值给当前位置)
初始:[ 5, 8, 3, 6, 4, 2, 1, 7] 操作次数
[ 8, 5, 6, 4, 3, 2, 7, 1] 7
[ 8, 6, 5, 4, 3, 7, 2, 1] 6
[ 8, 6, 5, 4, 7, 3, 2, 1] 5
[ 8, 6, 5, 7, 4, 3, 2, 1] 4
[ 8, 6, 7, 5, 4, 3, 2, 1] 3
[ 8, 7, 6, 5, 4, 3, 2, 1] 2
[ 8, 7, 6, 5, 4, 3, 2, 1] 1
[ 8, 7, 6, 5, 4, 3, 2, 1] 0
外层固定8个循环,内层固定7,6,5,4,3,2,1操作
时间复杂度为O(N^2)
2.选择排序
(比较出最小的元素,保存元素位置,和指定位置交换)
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理是每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。 选择排序是不稳定的排序方法(比如序列[5, 5, 3]第一次就将第一个[5]与[3]交换,导致第一个5挪动到第二个5后面)。
初始:[ 5, 8, 3, 6, 4, 2, 1, 7] 操作次数
[ 1, 8, 3, 6, 4, 2, 5, 7] 7
[ 1, 2, 3, 6, 4, 8, 5, 7] 6
[ 1, 2, 3, 6, 4, 8, 5, 7] 5
[ 1, 2, 3, 4, 6, 8, 5, 7] 4
[ 1, 2, 3, 4, 5, 8, 6, 7] 3
[ 1, 2, 3, 4, 5, 6, 8, 7] 2
[ 1, 2, 3, 4, 5, 6, 7, 8] 1
[ 1, 2, 3, 4, 5, 6, 7, 8] 0
外层固定8个循环,内层固定7,6,5,4,3,2,1操作
时间复杂度为O(N^2)
3.插入排序
有一个已经有序的数据序列,要求在这个已经排好的数据序列中插入一个数,但要求插入后此数据序列仍然有序,这个时候就要用到一种新的排序方法——插入排序法,插入排序的基本操作就是将一个数据插入到已经排好序的有序数据中,从而得到一个新的、个数加一的有序数据,算法适用于少量数据的排序,时间复杂度为O(n^2)。是稳定的排序方法。插入算法把要排序的数组分成两部分:第一部分包含了这个数组的所有元素,但将最后一个元素除外(让数组多一个空间才有插入的位置),而第二部分就只包含这一个元素(即待插入元素)。在第一部分排序完成后,再将这个最后元素插入到已排好序的第一部分中。
插入排序的基本思想是:每步将一个待排序的记录,按其关键码值的大小插入前面已经排序的文件中适当位置上,直到全部插入完为止。
1)普通版本插入排序(从1号元素位置开始与前一个元素做比较,较小就交换位置,较大就停止)------频繁交换位置(赋值三次)太耗费时间
2)改进版本插入排序(保存一个循环位置的元素副本,与当前位置的前一个位置元素作比较,只将当前元素赋值为前一个较大的元素,最后确认之后再将副本元素赋值)------减少赋值次数(之前的每一次交换减少为一次赋值)
初始:[ 5, 8, 3, 6, 4, 2, 1, 7] 操作次数
[ 5, 8, 3, 6, 4, 2, 1, 7] 0
[ 3, 5, 8, 6, 4, 2, 1, 7] 2
[ 3, 5, 6, 8, 4, 2, 1, 7] 1
[ 3, 4, 5, 6, 8, 2, 1, 7] 3
[ 2, 3, 4, 5, 6, 8, 1, 7] 5
[ 1, 2, 3, 4, 5, 6, 8, 7] 6
[ 1, 2, 3, 4, 5, 6, 7, 8] 1
外层固定7个循环,内层最多会有1,2,3,4,5,6,7操作(可以提前结束循环)
最好时间复杂度为O(N),最坏时间复杂度为O(N^2)
4.希尔排序
希尔排序(Shell's Sort)是插入排序的一种又称“缩小增量排序”(Diminishing Increment Sort),是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。该方法因D.L.Shell于1959年提出而得名。
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。 [1] (最后一个增量必须为1)
希尔排序(尽可能的在增量为1的排序之前用少量代价让数组接近完全排序)
增量为:4,2,1案例
(一)增量为4,外层循环(4次),中层循环(1次),内层循环操作0次
初始:[ 5, 8, 3, 6, 4, 2, 1, 7]
[ 4, 8, 3, 6, 5, 2, 1, 7] 1
[ 4, 2, 3, 6, 5, 8, 1, 7] 1
[ 4, 2, 1, 6, 5, 8, 3, 7] 1
[ 4, 2, 1, 6, 5, 8, 3, 7] 0
(二)增量为2,外层循环(2次),中层循环(3次),内层循环操作0次
初始:[ 4, 2, 1, 6, 5, 8, 3, 7]
[ 1, 2, 4, 6, 5, 8, 3, 7] 0
[ 1, 2, 4, 6, 5, 8, 3, 7] 0
[ 1, 2, 3, 6, 4, 8, 5, 7] 2
[ 1, 2, 3, 6, 4, 8, 5, 7] 0
[ 1, 2, 3, 6, 4, 8, 5, 7] 0
[ 1, 2, 3, 6, 4, 7, 5, 8]1
(三)增量为1,外层循环(1次),中层循环(7次),内层循环操作0次
初始:[ 1, 2, 3, 6, 4, 7, 5, 8]
[ 1, 2, 3, 6, 4, 7, 5, 8] 0
[ 1, 2, 3, 6, 4, 7, 5, 8] 0
[ 1, 2, 3, 6, 4, 7, 5, 8] 0
[ 1, 2, 3, 4, 6, 7, 5, 8] 1
[ 1, 2, 3, 4, 6, 7, 5, 8] 0
[ 1, 2, 3, 4, 5, 6, 7, 8] 2
[ 1, 2, 3, 4, 5, 6, 7, 8]0
最好时间复杂度为O(N),最坏时间复杂度为O(N^2),但是相对于插入排序快一些
|
public static void main(String[] args) { |
第三节、高级排序算法
1.归并排序
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
1)普通版本归并排序
|
/** |
2)改进版本归并排序-----两点改进
l 改进一,当数组数量小于16时,改成插入排序
l 改进二,当接近有序的排序的时候,需要修改部分操作
|
private static void mergeSort(int[] a, int l, int r) { |
|
private static void mergeSort(int[] a, int l, int r) { |
3)自底向上的归并排序
初始:[ 5, 8, 3, 6, 4, 2, 1, 7] 操作次数
2.快速排序
快速排序(Quicksort)是对冒泡排序的一种改进。
快速排序由C. A. R. Hoare在1962年提出。它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
1)普通版本
2)接近有序的序列,改进版(一)
3)重复值多的序列,改进版本(一)
4)重复值多的序列,改进版本(二),三路快速排序
初始:[ 5, 8, 3, 6, 4, 2, 1, 7] 操作次数
思考题
1)思考题逆序数------归并排序O(NlogN)
2)寻找数组中第N大的值------快速排序O(N)
第四节、堆和堆排序
二叉堆分为最小堆和最大堆两种,通过数组实现数据结构,数组从1开始。
堆更多场景用在动态维护上面
1.最大堆
最大堆是堆的两种形式之一。
根结点(亦称为堆顶)的关键字是堆里所有结点关键字中最大者,称为大根堆,又称最大堆(大顶堆)。
大根堆要求根节点的关键字既大于或等于左子树的关键字值,又大于或等于右子树的关键字值。
1)最大堆添加元素
对最后一个元素,下标为count元素进行上升操作(Shift Up)
2)最大堆堆中取出元素
堆中取出元素,然后将最后一个元素放到位置1,进行下降操作(Shift Down)操作
小优化,将交换位置改为赋值
3)最大堆堆排序
① 先将数组元素一个个存入堆中,再取出来放入数组中(NlogN)
② 数组转换为堆优化,先将数组复制为1为起始下标的数组,然后在非叶子节点的元素上下标为(count/2)进行下降(shift down)操作,这个名称为:heapify,在取出来放入堆中;heapify的时间复杂度为O(N)
4)原地堆排序
l 优化一(数组->最大堆):不再创建数组,从原本0开始的数组进行heapify
l 优化二(最大堆->排序好的数组):数组排序时,将最后一个元素和第一个元素交换位置,对第一个元素进行shift Down操作
5)最大索引堆
一个堆,堆放索引,寻找堆中索引所对应的优先级与其他堆中索引对应的优先级进行比较,然后再进行shift up或者shift down操作
一个数组,数组中放优先级,自始不会变化
1)入堆操作,出堆操作
2)改变堆的优先级操作,优先级是O(N)级别操作,如果对N个元素进行优先级改变就是O(N^2)操作,不理想
3)改变堆优先级操作(优化)

l 反向堆索引的数组
创建一个索引数组rev,rev的索引是index堆中的元素,rev的元素是index堆中的索引,通过找rev中的索引,直接找到对应的元素修改他的优先级,然后再回归到index堆中进行shift up或者shift down操作
可能存在的问题:堆中没有rev所对应的元素,即出堆之后将rev指向0
2.最小堆
自己实现吧!
排序算法总结
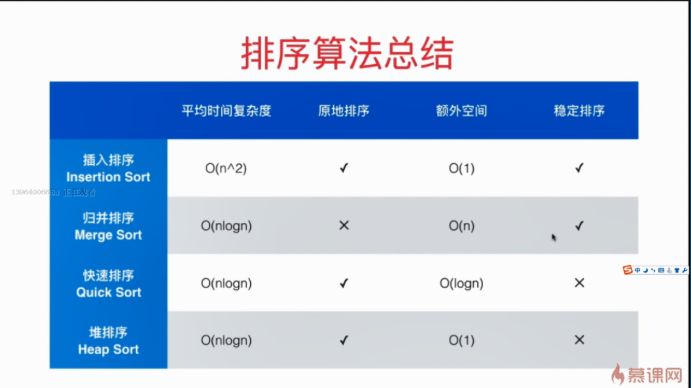
稳定性:举个例子:对于学生已经按照姓名排序之后,再按照成绩排序,成绩排序之后,相同成绩的学生还是按照姓名排好顺序,这就是稳定性
思考题
1.堆实现优先队列
2.堆实现人工智能自动攻击对象
3.100万元素中选出前100名
一个100的最小堆,最小的元素如果比要存的元素小,即当前要存的元素比较大,就吧当前元素存进去,再shift down操作,即N*logM时间复杂度
4.堆实现多路归并
5.d叉堆,本节实现的是二叉堆
6.统一以0为开始索引,1开始的索引是经典实现,但是不符合现实逻辑
7.一个最大堆,一个最小堆,同时处理一个数组中的元素
8.二项堆
9.斐波那契堆
第五节、二分搜索树
1.二分查找法(Binary Search)
二分查找也称折半查找(Binary Search),它是一种效率较高的查找方法。但是,折半查找要求线性表必须采用顺序存储结构,而且表中元素按关键字有序排列。 [1]
n 查找必须为顺序表,查找效率O(logN)
l 小bug:mid = (l+r)/2 l+r可能超过int的最大值
l 修改:mid = l + (r-l)/2
2.二叉搜索树
二叉查找树(Binary Search Tree),(又:二叉搜索树,二叉排序树)它或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。
n 查找表的实现 - 字典数据结构。
n 字典的key:value,key值不为整数时,增,删,改时间复杂度都是O(logN)。
n 二分搜索树:每个节点的键值大于左孩子,每个几点的兼职小于右孩子,以左右孩子为根的字数仍为二分搜索树。
n 二分查找树不一定为完全二叉树。
1)二分搜索树插入元素
n 一个个比较,如果比当前节点大,就查找右节点,比当前节点小,就查找左节点,如果不存在节点,就可以保存当前元素
n 如果存在重复值,即key值一样,即覆盖原来的value
2)二分搜索树查找元素
n 查找最小值:一直找二分搜索树的左节点
n 查找最大值:一直找二分搜索树的右节点
n 查找任意值:
3)二分搜索树的遍历
n 前序遍历
n 中序遍历
n 后序遍历
n 层序遍历:使用队列进行遍历
4)二分搜索树删除节点
n 删除最大值:
n 删除最小值:
n 删除任意一个节点:Hubbard Deletion,删除节点的右子树的最小值放到该位置;同理左子树的最大值




