图的最小生成树（java实现）

1.图的最小生成树（贪心算法）

我两个算法的输出都是数组表示的，当前的索引值和当前索引对应的数据就是通路，比如parent[2] = 5;即2和5之间有一个通路，第二个可能比较好理解，第一个有点混乱

是什么？

将一个有权图中的 所有顶点 都连接起来，并保证连接的边的 总权重最小，即最小生成树，最小生成树不唯一

为什么？

传入邻接矩阵，返回可以生成最小生成树的数据

我们有两种方式生成图的最小生成树1.普里姆（Prim）算法2.克鲁斯卡尔（Kruskal）算法

怎样做？

图片参考博客：https://blog.csdn.net/afei__/article/details/83316587

下面是普里姆算法的最小生成树

 

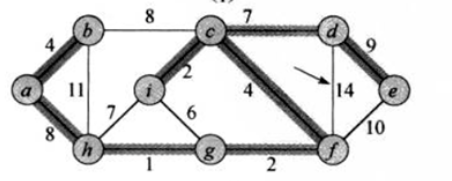
下面是克鲁斯卡尔算法的最小生成树：

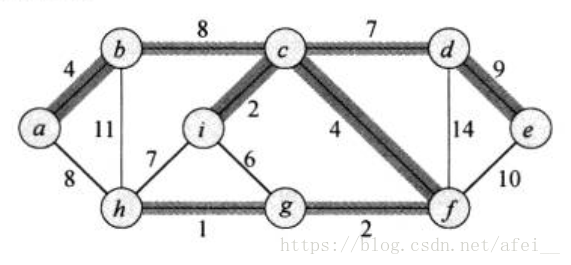
图的邻接矩阵表示法（无向图，上三角矩阵）

int[][] arr = new int[][]{
        {-1, 4, 0, 0, 0, 0, 0, 8, 0},
        {0, -1, 8, 0, 0, 0, 0, 11, 0},
        {0, 0, -1, 7, 0, 4, 0, 0, 2},
        {0, 0, 0, -1, 9, 14, 0, 0, 0},
        {0, 0, 0, 0, -1, 10, 0, 0, 0},
        {0, 0, 0, 0, 0, -1, 2, 0, 0},
        {0, 0, 0, 0, 0, 0, -1, 1, 6},
        {0, 0, 0, 0, 0, 0, 0, -1, 7},
        {0, 0, 0, 0, 0, 0, 0, 0, -1}
};

1.普里姆算法（加点法）

需求：求出最小生成树的权值

输入参数：二维数组arr（邻接矩阵），列表list（存放已经被加入的点），整型sum（存放权值）

输出参数：整型数组parent

1）先找一个起点，这个起点为任意一点，放入list中

2）如果list中不包含全部节点，进入循环

　　1>遍历list中节点，查找不存在list中的邻接节点的最小值，记录下begin和end

　　2>将begin和end放入数组中，较小值节点赋值给较大值所在数组位置

3）返回parent

 

 实现：

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

/**
 * 普里姆（Prim）算法
 *
 * @author Xiong YuSong
 * 2019/3/22 16:02
 */
public class Prim {

    public static void main(String[] args) {
        int[][] arr = new int[][]{
                {-1, 4, 0, 0, 0, 0, 0, 8, 0},
                {0, -1, 8, 0, 0, 0, 0, 11, 0},
                {0, 0, -1, 7, 0, 4, 0, 0, 2},
                {0, 0, 0, -1, 9, 14, 0, 0, 0},
                {0, 0, 0, 0, -1, 10, 0, 0, 0},
                {0, 0, 0, 0, 0, -1, 2, 0, 0},
                {0, 0, 0, 0, 0, 0, -1, 1, 6},
                {0, 0, 0, 0, 0, 0, 0, -1, 7},
                {0, 0, 0, 0, 0, 0, 0, 0, -1}
        };
        List<Integer> list = new ArrayList<>();
        //先将0放置在list中
        list.add(0);
        int begin = 0, end = 0, weight;
        int[] parent = new int[arr.length];
        for (int i = 0; i < arr.length; i++) {
            parent[i] = -1;
        }
        while (list.size() < arr.length) {
            weight = Integer.MAX_VALUE;
            for (Integer row : list) {
                for (int i = 0; i < arr.length; i++) {
                    if (!list.contains(i)) {
                        if (i >= row + 1) {
                            if (arr[row][i] > 0 && arr[row][i] < weight) {
                                begin = row;
                                end = i;
                                weight = arr[row][i];
                            }
                        } else if (i <= row - 1) {
                            //我这里只用了上三角矩阵，所以这里需要画蛇添足写这一部分
                            if (arr[i][row] > 0 && arr[i][row] < weight) {
                                begin = row;
                                end = i;
                                weight = arr[i][row];
                            }
                        }
                    }
                }
            }
            list.add(end);
            parent[end] = begin;
        }
        System.out.println(Arrays.toString(parent));
    }
}

 

2.克鲁斯卡尔算法（加边法）

需求：求出最小生成树的权值

构建类：Edge<begin,end,weight>三元组，根据weight（权值）排序

输入参数：存放有Edge的列表list，并查集parent

输出参数：并查集parent（最小生成树的数组表现形式）

原理：贪心算法的实现，程序中使用了并查集（判断两个集合中是否存在相同的数据）这种特殊的数据结构，使用数组实现

1）创建一个三元组<起始点，终止点，权值>，将邻接矩阵中数据放入三元组中，再放入list中，根据权值进行排序

2）创建变量count=0，整型数组parent

3）如果list中还存在值，则进行循环

　　1>判断begin和end是否存在于不同的集合中（判断是否在同一棵树中，即判断当前节点在并查集parent中的根节点是否为同一个）

　　2>如果存在不同的集合中，则将较小值节点赋值给较大值所在数组位置，较小值节点为较大值节点的父节点

4）返回parent

实现：

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.List;

/**
 * @author Xiong YuSong
 * 2019/3/22 17:04
 */
class Edge implements Comparable<Edge> {
    //起始点
    private int begin;
    //终止点
    private int end;
    //权值
    private int weight;

    public Edge(int begin, int end, int weight) {
        this.begin = begin;
        this.end = end;
        this.weight = weight;
    }

    public int getBegin() {
        return begin;
    }

    public void setBegin(int begin) {
        this.begin = begin;
    }

    public int getEnd() {
        return end;
    }

    public void setEnd(int end) {
        this.end = end;
    }

    public int getWeight() {
        return weight;
    }

    public void setWeight(int weight) {
        this.weight = weight;
    }

    @Override
    public int compareTo(Edge o) {
        if (o.weight > this.weight) {
            return -1;
        } else {
            return 1;
        }
    }
}

public class Kruskal {

    public static void main(String[] args) {
        //默认以a为根节点的最小生成树
        List<Edge> list = new ArrayList<>();
        int[][] arr = new int[][]{
                {-1, 4, 0, 0, 0, 0, 0, 8, 0},
                {0, -1, 8, 0, 0, 0, 0, 11, 0},
                {0, 0, -1, 7, 0, 4, 0, 0, 2},
                {0, 0, 0, -1, 9, 14, 0, 0, 0},
                {0, 0, 0, 0, -1, 10, 0, 0, 0},
                {0, 0, 0, 0, 0, -1, 2, 0, 0},
                {0, 0, 0, 0, 0, 0, -1, 1, 6},
                {0, 0, 0, 0, 0, 0, 0, -1, 7},
                {0, 0, 0, 0, 0, 0, 0, 0, -1}
        };
        for (int i = 0; i < arr.length; i++) {
            for (int j = i + 1; j < arr.length; j++) {
                if (arr[i][j] > 0) {
                    list.add(new Edge(i, j, arr[i][j]));
                }
            }
        }
        Collections.sort(list);
        //数组中每一个节点都只知道他的父节点是什么，-1表示不存在父节点，0位置是根节点
        int[] parent = new int[arr.length];
        for (int i = 1; i < arr.length; i++) {
            parent[i] = -1;
        }
        int m = 0, n = 0;
        for (Edge edge : list) {
            //寻找这两个点有没有相同的父节点
            m = find(parent, edge.getBegin());
            n = find(parent, edge.getEnd());
            if (m != n && parent[edge.getEnd()]>0) {
                parent[edge.getEnd()] = edge.getBegin();
            }
        }
        System.out.println(Arrays.toString(parent));
    }

    private static int find(int[] parent, int ch) {
        while (parent[ch] > 0) {
            ch = parent[ch];
        }
        return ch;
    }
}