机器学习(回归预测数值型数据)
之前介绍的分类的目标变量都是标称型数据,接下来我们将介绍连续型的数据并且作出预测,本篇介绍的是线性回归,接下来引入局部平滑技术,能够更好地拟合数据
本篇我们主要讨论欠拟合情况下的缩减的技术,探讨偏差和方差的概念。
优点:结构易于理解,计算上不复杂
缺点:对非线性的数据拟合不好
适合数值型和标称型数据
有回归方程,求回归方程的回归系数的过程就是回归,一旦有了回归系数,再给定了输入,做预测就非常容易。具体做法就是回归系数乘以输入数据,再将结果全部加到一起,就得到预测值
机器学习算法的基本任务就是预测,预测目标按照数据类型可以分为两类:一种是标称型数据(通常表现为类标签),另一种是连续型数据(例如房价或者销售量等等)。针对标称型数据的预测就是我们常说的分类,针对数值型数据的预测就是回归了。这里有一个特殊的算法需要注意,逻辑回归(logistic regression)是一种用来分类的算法,那为什么又叫“回归”呢?这是因为逻辑回归是通过拟合曲线来进行分类的。也就是说,逻辑回归只不过在拟合曲线的过程中采用了回归的思想,其本质上仍然是分类算法
这个简单的式子就叫回归方程,其中0.7和0.19称为回归系数,面积和房子的朝向称为特征。有了这些概念,我们就可以说,回归实际上就是求回归系数的过程。在这里我们看到,房价和面积以及房子的朝向这两个特征呈线性关系,这种情况我们称之为线性回归。当然还存在非线性回归,在这种情况下会考虑特征之间出现非线性操作的可能性(比如相乘或者相除),由于情况有点复杂,不在这篇文章的讨论范围之内。
简便起见,我们规定代表输入数据的矩阵为XX (维度为m*n,m为样本数,n为特征维度),回归系数向量为 θθ(维度为n*1)。对于给定的数据矩阵XX ,其预测结果由:Y=XθY=Xθ 这个式子给出。我们手里有一些现成的x和y作为训练集,那么如何根据训练集找到合适的回归系数向量θθ是我们要考虑的首要问题,一旦找到θθ,预测问题就迎刃而解了。在实际应用中,我们通常认为能带来最小平方误差的θθ就是我们所要寻找的回归系数向量。平方误差指的是预测值与真实值的差的平方。采用平方这种形式的目的在于规避正负误差的互相抵消。所以,我们的目标函数如下所示:
这里的m代表训练样本的总数。对这个函数的求解有很多方法,由于网络上对于详细解法的相关资料太少,下面展示一种利用正规方程组的解法: 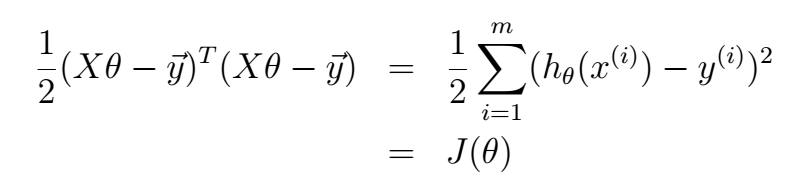
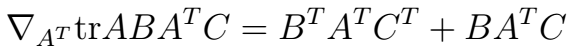
针对上式不太清楚的朋友可以看我之前写的这篇博文:http://blog.csdn.net/qrlhl/article/details/47758509。根据以上式子,解法如下:
令其等于0,即可得:θ=(XTX)−1XTyθ=(XTX)−1XTy 。有一些需要说明的地方:第三步是根据实数的迹和等于本身这一事实推导出的(括号中的每一项都为实数),第四步是根据式(2)推导出来的。第五步是根据式(1)推导出来的,其中的C为单位矩阵II。这样,我们就得到了根据训练集求得回归系数矩阵θθ的方程。这种方法的特点是简明易懂,不过缺点也很明显,就是XTXXTX 这一项不一定可以顺利的求逆。由于只有满秩才可以求逆,这对数据矩阵XX提出了一定的要求。有人也许会问XTXXTX不是满秩的情况下怎么办?这个时候就要用到岭回归(ridge regression)了,这一部分留到下次再讲。
贴上代码
from numpy import * def loadDataSet(fileName): #general function to parse tab -delimited floats numFeat = len(open(fileName).readline().split('\t')) - 1 #get number of fields dataMat = []; labelMat = [] fr = open(fileName) for line in fr.readlines(): lineArr =[] curLine = line.strip().split('\t') for i in range(numFeat): lineArr.append(float(curLine[i])) dataMat.append(lineArr) labelMat.append(float(curLine[-1])) return dataMat,labelMat def standRegres(xArr,yArr): xMat = mat(xArr); yMat = mat(yArr).T xTx = xMat.T*xMat if linalg.det(xTx) == 0.0: print "This matrix is singular, cannot do inverse" return ws = xTx.I * (xMat.T*yMat) return ws def lwlr(testPoint,xArr,yArr,k=1.0): xMat = mat(xArr); yMat = mat(yArr).T m = shape(xMat)[0] weights = mat(eye((m))) for j in range(m): #next 2 lines create weights matrix diffMat = testPoint - xMat[j,:] # weights[j,j] = exp(diffMat*diffMat.T/(-2.0*k**2)) xTx = xMat.T * (weights * xMat) if linalg.det(xTx) == 0.0: print "This matrix is singular, cannot do inverse" return ws = xTx.I * (xMat.T * (weights * yMat)) return testPoint * ws def lwlrTest(testArr,xArr,yArr,k=1.0): #loops over all the data points and applies lwlr to each one m = shape(testArr)[0] yHat = zeros(m) for i in range(m): yHat[i] = lwlr(testArr[i],xArr,yArr,k) return yHat def lwlrTestPlot(xArr,yArr,k=1.0): #same thing as lwlrTest except it sorts X first yHat = zeros(shape(yArr)) #easier for plotting xCopy = mat(xArr) xCopy.sort(0) for i in range(shape(xArr)[0]): yHat[i] = lwlr(xCopy[i],xArr,yArr,k) return yHat,xCopy def rssError(yArr,yHatArr): #yArr and yHatArr both need to be arrays return ((yArr-yHatArr)**2).sum() def ridgeRegres(xMat,yMat,lam=0.2): xTx = xMat.T*xMat denom = xTx + eye(shape(xMat)[1])*lam if linalg.det(denom) == 0.0: print "This matrix is singular, cannot do inverse" return ws = denom.I * (xMat.T*yMat) return ws def ridgeTest(xArr,yArr): xMat = mat(xArr); yMat=mat(yArr).T yMean = mean(yMat,0) yMat = yMat - yMean #to eliminate X0 take mean off of Y #regularize X's xMeans = mean(xMat,0) #calc mean then subtract it off xVar = var(xMat,0) #calc variance of Xi then divide by it xMat = (xMat - xMeans)/xVar numTestPts = 30 wMat = zeros((numTestPts,shape(xMat)[1])) for i in range(numTestPts): ws = ridgeRegres(xMat,yMat,exp(i-10)) wMat[i,:]=ws.T return wMat def regularize(xMat):#regularize by columns inMat = xMat.copy() inMeans = mean(inMat,0) #calc mean then subtract it off inVar = var(inMat,0) #calc variance of Xi then divide by it inMat = (inMat - inMeans)/inVar return inMat def stageWise(xArr,yArr,eps=0.01,numIt=100): xMat = mat(xArr); yMat=mat(yArr).T yMean = mean(yMat,0) yMat = yMat - yMean #can also regularize ys but will get smaller coef xMat = regularize(xMat) m,n=shape(xMat) #returnMat = zeros((numIt,n)) #testing code remove ws = zeros((n,1)); wsTest = ws.copy(); wsMax = ws.copy() for i in range(numIt): print ws.T lowestError = inf; for j in range(n): for sign in [-1,1]: wsTest = ws.copy() wsTest[j] += eps*sign yTest = xMat*wsTest rssE = rssError(yMat.A,yTest.A) if rssE < lowestError: lowestError = rssE wsMax = wsTest ws = wsMax.copy() #returnMat[i,:]=ws.T #return returnMat #def scrapePage(inFile,outFile,yr,numPce,origPrc): # from BeautifulSoup import BeautifulSoup # fr = open(inFile); fw=open(outFile,'a') #a is append mode writing # soup = BeautifulSoup(fr.read()) # i=1 # currentRow = soup.findAll('table', r="%d" % i) # while(len(currentRow)!=0): # title = currentRow[0].findAll('a')[1].text # lwrTitle = title.lower() # if (lwrTitle.find('new') > -1) or (lwrTitle.find('nisb') > -1): # newFlag = 1.0 # else: # newFlag = 0.0 # soldUnicde = currentRow[0].findAll('td')[3].findAll('span') # if len(soldUnicde)==0: # print "item #%d did not sell" % i # else: # soldPrice = currentRow[0].findAll('td')[4] # priceStr = soldPrice.text # priceStr = priceStr.replace('$','') #strips out $ # priceStr = priceStr.replace(',','') #strips out , # if len(soldPrice)>1: # priceStr = priceStr.replace('Free shipping', '') #strips out Free Shipping # print "%s\t%d\t%s" % (priceStr,newFlag,title) # fw.write("%d\t%d\t%d\t%f\t%s\n" % (yr,numPce,newFlag,origPrc,priceStr)) # i += 1 # currentRow = soup.findAll('table', r="%d" % i) # fw.close() from time import sleep import json import urllib2 def searchForSet(retX, retY, setNum, yr, numPce, origPrc): sleep(10) myAPIstr = 'AIzaSyD2cR2KFyx12hXu6PFU-wrWot3NXvko8vY' searchURL = 'https://www.googleapis.com/shopping/search/v1/public/products?key=%s&country=US&q=lego+%d&alt=json' % (myAPIstr, setNum) pg = urllib2.urlopen(searchURL) retDict = json.loads(pg.read()) for i in range(len(retDict['items'])): try: currItem = retDict['items'][i] if currItem['product']['condition'] == 'new': newFlag = 1 else: newFlag = 0 listOfInv = currItem['product']['inventories'] for item in listOfInv: sellingPrice = item['price'] if sellingPrice > origPrc * 0.5: print "%d\t%d\t%d\t%f\t%f" % (yr,numPce,newFlag,origPrc, sellingPrice) retX.append([yr, numPce, newFlag, origPrc]) retY.append(sellingPrice) except: print 'problem with item %d' % i def setDataCollect(retX, retY): searchForSet(retX, retY, 8288, 2006, 800, 49.99) searchForSet(retX, retY, 10030, 2002, 3096, 269.99) searchForSet(retX, retY, 10179, 2007, 5195, 499.99) searchForSet(retX, retY, 10181, 2007, 3428, 199.99) searchForSet(retX, retY, 10189, 2008, 5922, 299.99) searchForSet(retX, retY, 10196, 2009, 3263, 249.99) def crossValidation(xArr,yArr,numVal=10): m = len(yArr) indexList = range(m) errorMat = zeros((numVal,30))#create error mat 30columns numVal rows for i in range(numVal): trainX=[]; trainY=[] testX = []; testY = [] random.shuffle(indexList) for j in range(m):#create training set based on first 90% of values in indexList if j < m*0.9: trainX.append(xArr[indexList[j]]) trainY.append(yArr[indexList[j]]) else: testX.append(xArr[indexList[j]]) testY.append(yArr[indexList[j]]) wMat = ridgeTest(trainX,trainY) #get 30 weight vectors from ridge for k in range(30):#loop over all of the ridge estimates matTestX = mat(testX); matTrainX=mat(trainX) meanTrain = mean(matTrainX,0) varTrain = var(matTrainX,0) matTestX = (matTestX-meanTrain)/varTrain #regularize test with training params yEst = matTestX * mat(wMat[k,:]).T + mean(trainY)#test ridge results and store errorMat[i,k]=rssError(yEst.T.A,array(testY)) #print errorMat[i,k] meanErrors = mean(errorMat,0)#calc avg performance of the different ridge weight vectors minMean = float(min(meanErrors)) bestWeights = wMat[nonzero(meanErrors==minMean)] #can unregularize to get model #when we regularized we wrote Xreg = (x-meanX)/var(x) #we can now write in terms of x not Xreg: x*w/var(x) - meanX/var(x) +meanY xMat = mat(xArr); yMat=mat(yArr).T meanX = mean(xMat,0); varX = var(xMat,0) unReg = bestWeights/varX print "the best model from Ridge Regression is:\n",unReg print "with constant term: ",-1*sum(multiply(meanX,unReg)) + mean(yMat)