数据结构与算法->树->2-3-4树的查找,添加,删除(Java)
代码: 兵马未动,粮草先行
作者: 传说中的汽水枪
如有错误,请留言指正,欢迎一起探讨.
转载请注明出处.
目录
一. 2-3-4树的定义
二. 2-3-4树数据结构定义
三. 2-3-4树的可以得到几个推论
四. 2-3-4树节点keys/subNodes相关方法定义与解释
五. 2-3-4树节点性质属性相关方法定义
六. 2-3-4树查找逻辑解释和代码实现
七. 2-3-4树插入逻辑解释和代码实现
八. 2-3-4树删除逻辑解释和代码实现
摘要
网上有一大堆介绍了2-3-4树这种数据结构,但是没有给出代码实现,本系列文章是实现2-3-4树的查找/插入/删除操作!
一. 2-3-4树的定义
2-3-4树是一种阶为4的B树。它是一种自平衡的数据结构,可以保证在O(lgn)的时间内完成查找、插入和删除操作。它主要满足以下性质:
(1)每个节点每个节点有1、2或3个key,分别称为2(孩子)节点,3(孩子)节点,4(孩子)节点。
(2)所有叶子节点到根节点的长度一致(也就是说叶子节点都在同一层)。
(3)每个节点的key从左到右保持了从小到大的顺序,两个key之间的子树中所有的key一定大于它的父节点的左key,小于父节点的右key。
(摘自:http://blog.csdn.net/xiaokang123456kao/article/details/54379868)
此系列文章,不考虑key相同的情况.
二. 2-3-4树数据结构定义
定义了3个类, 分别是: TwoThreeFourTree, Node, DataItem
Node和DataItem是TwoThreeFourTree的类中类
图一: 3个分别指的相关数据

Java代码一
/** * * @Description : 2-3-4树 * @author : Rush.D.Xzj * @CreateDate : 2017-07-25 18:06:09 * */ public class TwoThreeFourTree { /**根节点*/ private Node root; /**TwoThreeFourTree.LOG*/ private static final Log LOG = LogFactory.getLog(TwoThreeFourTree.class); /** * * @Description : 2-3-4树的节点 * @author : Rush.D.Xzj * @CreateDate : 2017-07-05 18:08:30 * */ public class Node { public static final int MAX_CHILD_COUNT = 4; /**最大的字节点个数*/ private int maxChildCount; /**父节点*/ private Node parent; /**count = 0, 2, 3, 4*/ private List<Node> subNodes; /**count = 1, 2, 3, 此数据的数目不可能为空!*/ /**在非叶子节点的情况下, keys.size() + 1 = subNodes.size()*/ private List<DataItem> keys; public Node(DataItem dataItem) { this.subNodes = new ArrayList<Node>(); this.keys = new ArrayList<DataItem>(); this.parent = null; this.keys.add(dataItem); this.maxChildCount = MAX_CHILD_COUNT; } public Node(int key) { this.subNodes = new ArrayList<Node>(); this.keys = new ArrayList<DataItem>(); this.parent = null; this.keys.add(new DataItem(key)); this.maxChildCount = MAX_CHILD_COUNT; } } /** * * @Description : 数据项封装 * @author : Rush.D.Xzj * @CreateDate : 2017-07-05 18:25:11 * */ public class DataItem { public int key; public DataItem(int key) { this.key = key; } } }
三. 2-3-4树的可以得到几个推论
根据代码一的相关注释我们可以得出以下的推论
推论1: keys.size() >= 1
推论2: 在非叶子节点的情况下, keys.size() + 1 == subNodes.size()
推论3: 因为是搜索树,所以某个key(keyA)下面的左边所有树的节点中的所有key都小于keyA,同理:keyA下面的右边所有树的节点中的所有key都大于keyA
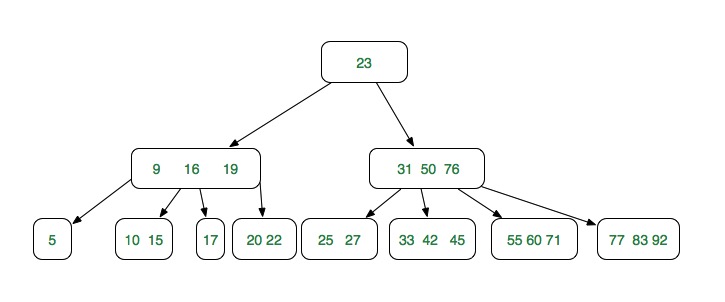
图二: 示例树

以图二来中的树来举例推论3
(55,60,71)节点不可能是(49,60,71)
因为49小于(23,50)节点中的50了.
四. 2-3-4树节点keys/subNodes相关方法定义与解释
在Node类中定义如下的方法:
public Node getSubNode(int index) { return this.subNodes.get(index); } public int subNodeSize() { return this.subNodes.size(); } public void addSubNode(int index, Node node) { if (node != null) { this.subNodes.add(index, node); node.parent = this; } } public void removeSubNode(int index) { this.subNodes.remove(index); } public void removeSubNode(Node node) { this.subNodes.remove(node); } public int indexOfNode(Node node) { return this.subNodes.indexOf(node); } public void clearSubNodes() { this.subNodes.clear(); } public Node getFirstSubNode() { if (this.subNodes.size() == 0) { return null; } return this.subNodes.get(0); } public Node getLastSubNode() { if (this.subNodes.size() == 0) { return null; } return this.subNodes.get(this.subNodes.size() - 1); } public void removeFirstSubNode() { if (this.subNodes.size() != 0) { this.subNodes.remove(0); } } public void removeLastSubNode() { if (this.subNodes.size() != 0) { this.subNodes.remove(this.subNodes.size() - 1); } } public void addToFirstSubNode(Node subNode) { if (subNode != null) { this.subNodes.add(0, subNode); subNode.parent = this; } } public void addToLastSubNode(Node subNode) { if (subNode != null) { this.subNodes.add(subNode); subNode.parent = this; } } public DataItem getKey(int index) { return this.keys.get(index); } public int keySize() { return this.keys.size(); } public void addKey(int index, DataItem dataItem) { if (dataItem != null) { this.keys.add(index, dataItem); } } public void removeKey(int index) { this.keys.remove(index); } public void removeKey(DataItem dataItem) { DataItem removeItem = null; for (int i = 0; i < this.keySize(); i++) { DataItem tmp = this.keys.get(i); if (tmp.key == dataItem.key) { removeItem = tmp; break; } } this.keys.remove(removeItem); } public int indexOfKey(DataItem dataItem) { return this.keys.indexOf(dataItem); } public void clearKeys() { this.keys.clear(); } public DataItem getFirstKey() { if (this.keys.size() == 0) { return null; } return this.keys.get(0); } public DataItem getLastKey() { if (this.keys.size() == 0) { return null; } return this.keys.get(this.keys.size() - 1); } public void removeFirstKey() { if (this.keys.size() != 0) { this.keys.remove(0); } } public void removeLastKey() { if (this.keys.size() != 0) { this.keys.remove(this.keys.size() - 1); } } public void addToFirstKey(DataItem dataItem) { if (dataItem != null) { this.keys.add(0, dataItem); } } public void addToLastKey(DataItem dataItem) { if (dataItem != null) { this.keys.add(dataItem); } }
认真看完代码发现上述N个方法就是简单的对Java List(keys, subNodes)的相关函数二次包装(public void removeKey(DatItem dataItem) 这个函数除外).
有的读者可能会有疑惑为什么要定义这样的函数?
此问题可以留在最后再给出答案.
五. 2-3-4树节点性质属性相关方法定义
Node类中的相关方法
/** * * @Description : 是否是满节点,keys数目必须是this.maxChildCount-1才是满节点 * @return : boolean * */ public boolean isFull() { return this.keySize() == this.maxChildCount - 1; } /** * * @Description : 是否是叶子节点,子节点数目必须是0 * @return : boolean * */ public boolean isLeaf() { return this.subNodeSize() == 0; } /** * * @Description : 2节点(包含子节点或不包含) * @return : boolean * */ public boolean isTwoKey() { return this.keySize() == 1; } /** * * @Description : 3节点(包含子节点或不包含) * @return : boolean * */ public boolean isThreeKey() { return this.keySize() == 2; } /** * * @Description : 4节点(包含子节点或不包含) * @return : boolean * */ public boolean isFourKey() { return this.keySize() == 3; } /** * * @Description : 2节点 * @return : boolean * */ public boolean isTwoNode() { return this.subNodeSize() == 2; } /** * * @Description : 3节点 * @return : boolean * */ public boolean isThreeNode() { return this.subNodeSize() == 3; } /** * * @Description : 4节点 * @return : boolean * */ public boolean isFourNode() { return this.subNodeSize() == 4; }
因为推论2,实际上上面的相关方法实际上还有另外一种判断,例如:
public boolean isFourNode() { return this.keySize() == 3; }
六. 2-3-4树查找逻辑解释和代码实现
查找逻辑算法:
1. 从根节点设置为当前节点
2. 如果当前节点找到了,就返回
3. 如果当前没有找到, 获取离的最近的一个
4. 重复步骤2,3
以图二的树来说明步骤3
假设找17:
1.先在节点(23,50)找
2.没有找到, 得到一个最近的一个index为0(因为17<23) ,这时候直接跳转到节点(9,16,19)
3.在节点(9,16,19)找,没有找到,得到一个最近的一个index为2(因为17<19),这个时候直接跳转到节点(17)
4.在节点(17)找到17 查找结束
再来一次假设:
假设找76:
1.先在节点(23,50)找
2.没有找到, 得到一个最近的一个index为2(因为76>50, 所以是该节点最后一个子节点找) ,这时候直接跳转到节点(76)
3.在节点(76)找到76 查找结束
上述举的2个例子有一个关键是找到那个index,直接上代码
在Node类中添加如下代码:
/**是否找到*/ public static final String VALUE_FIND = "VALUE_FIND"; /**相关的keyIndex*/ public static final String VALUE_INDEX = "VALUE_INDEX"; /** * * @Description : 查找位置和相关的index * @param dataItem : 需要查找的数据 * @return : java.util.Map * */ public Map keyIndex(DataItem dataItem) { Map result = new HashMap(); // 默认的设置未找到 result.put(VALUE_FIND, false); int index = 0; for (; index < this.keySize(); index ++) { DataItem tmpItem = this.getKey(index); if (dataItem.key == tmpItem.key) { // 如果等于就跳出循环,并且设置为true result.put(VALUE_FIND, true); break; } else if (dataItem.key < tmpItem.key) { // 如果小于了就直接跳出循环 break; } } // 也有可能需要查找的数据比此节点所有的数据都大 // 因此循环结束后都没有执行break // 此时的index就是keySize() result.put(VALUE_INDEX, index); return result; }
注意注释中这样的一段话:
此时的index就是keySize()
真好可以对应:假设找70的例子,是印证了推论2.
在TwoThreeFourTree中添加查找函数:
public DataItem find(int key) { if (this.root == null) { return null; } else { DataItem dataItem = new DataItem(key); DataItem findItem = this.find(this.root, dataItem); return findItem; } } private DataItem find(Node node, DataItem dataItem) { if (node == null) { return null; } // 请注意这个函数的注释 Map keyMap = node.keyIndex(dataItem); boolean find = (Boolean)(keyMap.get(Node.VALUE_FIND)); int keyIndex = (Integer)(keyMap.get(Node.VALUE_INDEX)); if (find) { return node.getKey(keyIndex); } // 如果上述没有找到,那么如果代码运行到这里, // keyIndex = keySize // 那么subNodes.get(keyIndex), // 就是subNodes的最后一个元素(因为2-3-4树,subNodes的数目不是0就是keySize + 1) // 如果keyIndex // 如果没有字节点,就表示没有找到 if (node.subNodeSize() == 0) { return null; } Node subNode = node.getSubNode(keyIndex); // 重复上述这个过程 return this.find(subNode, dataItem); }
七. 2-3-4树插入逻辑解释和代码实现
本博文用的插入算法是: 带有预分裂的插入算法.
算法的基本思路是:
1. 如果找到已经存在此值,那么就直接退出
2. 如果没有找到,从根节点开始遍历
3.如果是满节点,那么先分裂此节点(7.1)
4.如果是叶子节点,那么就在合适的位置插入(7.4)
5.否则,继续寻找合适的位置(7.3)
7.1 满节点的分裂
分裂示意图:
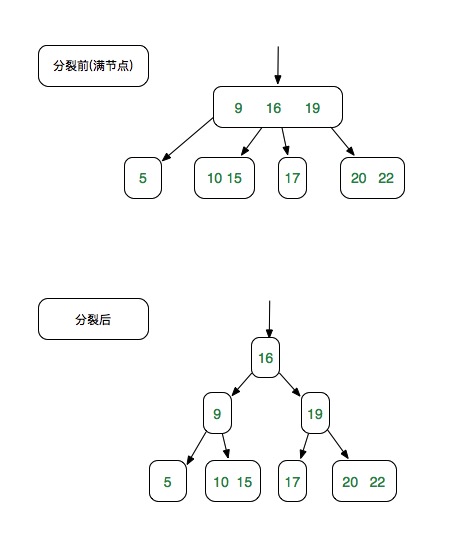
具体代码实现如下(Node类中):
public void connectNode(Node childNode) { if (childNode != null) { this.addToLastSubNode(childNode); } } public void connectNodes(List<Node> nodes) { for (Node node : nodes) { this.connectNode(node); } } /** * * @Description : 必须是满节点才能分裂 * 节点分裂的时候,会分裂成3个新的节点,此节点相当于没有用了 * @return : com.rush.structure.TwoThreeFourTree.Node * */ public Node split() { DataItem leftItem = this.getKey(0); DataItem midItem = this.getKey(1); DataItem rightItem = this.getKey(2); Node resultNode = new Node(midItem); Node resultFirstChildNode = new Node(leftItem); Node resultSecondChildNode = new Node(rightItem); // 原来的subNode,一人一半 for (int i = 0; i < this.subNodeSize(); i++) { Node subNode = this.getSubNode(i); if (i < 2) { resultFirstChildNode.connectNode(subNode); } else { resultSecondChildNode.connectNode(subNode); } } resultNode.connectNode(resultFirstChildNode); resultNode.connectNode(resultSecondChildNode); return resultNode; }
7.2 分裂后的节点处理
当约到7.1的情况后,分裂实际上是多了一层.所以要处理这个多了这一层分两种情况.
根据2-3-4树的相关性质和预分裂的处理,可以得到:
节点A: 分裂的节点的父节点, 为空或者一定不是满节点
节点B: 分裂的节点(示例图中的:9,16,19节点),一定是满节点
节点C: 节点B分裂后得到的节点(示例图中的16节点),一定是2节点,且此节点的2个子节点也一定是2节点
如果节点B是根节点那么就不处理,表示此2-3-4树经过插入操作后,增加了一层,此时的根节点就是节点C.
如果节点B不是根节点,那么节点A需要吸收节点C,使新添加的层消失掉,这样才满足2-3-4树性质.
以下代码就是节点吸收函数(Node类中).
public void absorbNode(Node oldNode, Node newNode) { int index = this.indexOfNode(oldNode); this.removeSubNode(oldNode); int keyIndex = index; int subNodeStartIndex = index; this.addKey(keyIndex, newNode.getFirstKey()); for (int i = 0; i < newNode.subNodeSize() ; i++) { Node tmpNode = newNode.getSubNode(i); // 把newNode下的节点添加到this的节点下 this.addSubNode(i + subNodeStartIndex, tmpNode); // 更新父节点 tmpNode.parent = this; } }
7.3 继续寻找合适的位置
代码如下(Node类中):
public Node getSuitableNode(DataItem dataItem) { int index = 0; for (; index < this.keySize(); index ++) { DataItem tmpDataItem = this.getKey(index); if (dataItem.key < tmpDataItem.key) { break; } } return this.getSubNode(index); }

例如
如果dataItem是3, 那么就返回子节点1
如果dataItem是11, 那么就返回子节点2
如果dataItem是17, 那么就返回子节点3
如果dataItem是20, 那么就返回子节点4
7.4 是叶子节点,那么就在合适的位置插入(Node类中)
public void insert(DataItem dataItem) { int index = 0; for (; index < this.keySize(); index++) { DataItem tmpItem = this.getKey(index); if (tmpItem.key > dataItem.key) { break; } } // 此处逻辑跟find类似 // list.add(list.size(), key) 等价于 list.add(key) this.addKey(index, dataItem); }
最后是2-3-4的插入实现(TwoThreeFourTree类中):
public boolean insert(int key) { if (this.find(key) != null) { return false; } this.root = this.insert(this.root, key); return true; } private Node insert(Node node, int key) { DataItem dataItem = new DataItem(key); if (node == null) { Node newNode = new Node(dataItem); return newNode; } Node resultNode = node; Node curNode = node; while (true) { if (curNode.isFull()) { Node curNodeParent = curNode.parent; Node splitNode = curNode.split(); // 当前节点是根节点 if (curNodeParent == null) { resultNode = splitNode; } else { curNodeParent.absorbNode(curNode, splitNode); } curNode = splitNode; } else if (curNode.isLeaf()) { // 跳出循环 break; } else { curNode = curNode.getSuitableNode(dataItem); } } curNode.insert(dataItem); return resultNode; }
八. 2-3-4树删除逻辑解释和代码实现
最简单的删除元素是直接删除非2节点的叶子节点上的元素,所以在删除元素的时候,我们需要把待删除的元素给想办法替换到叶子节点上.
称之为预合并的删除方法.
为了实现删除功能,我们需要定义实现如下的功能
8.1 树的高度
跟其他的树的高度概念一样
直接给出实现(TwoThreeFourTree)
public int height() { return this.height(this.root); } private int height(Node node) { if (node == null) { return 0; } if (node.subNodeSize() == 0) { return 1; } return 1 + this.height(node.getFirstSubNode()); }
8.2 某个元素在2-3-4树中的路径
我定义了一个路径的概念,先给出结果(基于示例图二),然后再解释一下这个路径
2017-09-18 13:32:07 INFO testPath(TwoThreeFourTreeTest.java:95) - key:20,path:[0, 0, 3] 2017-09-18 13:32:07 INFO testPath(TwoThreeFourTreeTest.java:99) - key:42,path:[0, 1, 1] 2017-09-18 13:32:07 INFO testPath(TwoThreeFourTreeTest.java:105) - key:45,path:[0, 1, 1] 2017-09-18 13:32:07 INFO testPath(TwoThreeFourTreeTest.java:111) - key:23,path:[0, 0, 0] 2017-09-18 13:32:07 INFO testPath(TwoThreeFourTreeTest.java:117) - key:50,path:[0, 1, 1] 2017-09-18 13:32:07 INFO testPath(TwoThreeFourTreeTest.java:123) - key:16,path:[0, 0, 1] 2017-09-18 13:32:07 INFO testPath(TwoThreeFourTreeTest.java:128) - key:19,path:[0, 0, 2] 2017-09-18 13:32:07 INFO testPath(TwoThreeFourTreeTest.java:133) - key:31,path:[0, 1, 0]
8.2.1 路径的长度等于高度
8.2.2 路径第一个元素都是0
8.2.3 路径下标为i(i > 0)的值表示i - 1的那个节点的第i个元素.(下标值是从0开始的!!!!!)
举例来说, 对于42 这个key值的路径是 [0,1,1]
路径数组下标为0,值为0表示是根节点(23,50)
路径数组下标为1,值为1表示是(31)节点, 也就是(23,50)节点的下标值为1的子节点
路径数组下标为2,值为1表示是(33,42,45)节点,也就是(31)节点的下标值为1的子节点
上面的这个逻辑好绕,慢慢的看
8.2.4 如果key值不在叶子节点中,那么后面的都是0
举例来说, 对于42 这个key值的路径是 [0,1,0]
路径数组下标为0,值为0表示是根节点(23,50)
路径数组下标为1,值为1表示是(31)节点, 也就是(23,50)节点的下标值为1的子节点
路径数组下标为2,值为0表示是(25,27)节点,也就是(31)节点的下标值为1的子节点
以下是路径函数(TwoThreeFourTree):
public List<Integer> path(int key) { DataItem dataItem = new DataItem(key); List<Integer> keyIndexes = new ArrayList<Integer>(); int height = this.height(); int nodeIndex = 0; Node curNode = this.root; // 第一层 肯定是根节点并且是第0个元素 keyIndexes.add(nodeIndex); boolean find = false; // 当找到的时候,它的子节点对应的keyIndex int findNextIndex = 0; // 可以把结束条件变成 i < height + 1 // 但是为了输出在最后叶子节点找到的信息,所以变成了 i < height for (int i = 0; i < height; i++) { // 已经提前找到就是默认此key值的左边的那个子元素 // 不是最后一层 if (find && (i != height - 1)) { keyIndexes.add(findNextIndex); // 这个时候就需要置为0 findNextIndex = 0; continue; } int keyIndex = 0; // 遍历当前节点的所有key for (; keyIndex < curNode.keySize(); keyIndex++) { DataItem tmpItem = curNode.getKey(keyIndex); if (dataItem.key < tmpItem.key) { break; } else if (dataItem.key == tmpItem.key) { find = true; findNextIndex = keyIndex; break; } else { } } // 不是最后一层 if (i != height - 1) { keyIndexes.add(keyIndex); // 获取下一个字节点 curNode = curNode.getSubNode(keyIndex); } } return keyIndexes; }
所以说预合并的删除就是需要把路径中的2节点全部转换成3,4节点.
8.3 节点的转换
如何把路径中的2节点全部转换成3,4节点?
转换的方式主要有两种,
8.3.1 从节点的兄弟节点(此兄弟节点是2节点)给合并成4节点(还有一个是从父节点偷的),
8.3.2 从兄弟节点(此兄弟节点是3节点或者4节点)偷节点变成3节点.这一块还要涉及到跟父节点的变化,具体可看效果图
8.3.1 的效果图(对(31)节点的转换,合并(76)节点)
8.3.2 的效果图1(对(5)节点的转换,从右边偷,偷(10,15)节点)

8.3.2 的效果图2(对(17)节点的转换,从左边边偷,偷(10,15)节点)

转换函数(Node):
public void transfer() { if (this.parent == null || !this.isTwoKey()) { return; } int parentSubNodeSize = this.parent.subNodeSize(); int subNodeIndex = this.parent.indexOfNode(this); Node leftNode = null; Node rightNode = null; // 转换方式 // 1. 此节点和另一个兄弟节点都是2节点,把右边的节点给合并过来 // 2. 此节点和另一个兄弟节点都是2节点,把左边的节点给合并过来 // 3. 从右边兄弟节点偷一个值 // 4. 从左边兄弟节点偷一个值 int transferType = 1; int parentKeyIndex = 0; // 表示此节点在父节点的最左边 if (subNodeIndex == 0) { parentKeyIndex = 0; leftNode = this; rightNode = this.parent.getSubNode(1); if (rightNode.isTwoKey()) { transferType = 1; } else { transferType = 3; } } else if (subNodeIndex == parentSubNodeSize - 1) { parentKeyIndex = this.parent.keySize() - 1; leftNode = this.parent.getSubNode(subNodeIndex - 1); rightNode = this; if (leftNode.isTwoKey()) { transferType = 2; } else { transferType = 4; } } else { // 肯定有左右2个兄弟节点 Node thisLeftBrotherNode = this.parent.getSubNode(subNodeIndex - 1); Node thisRightBrotherNode = this.parent.getSubNode(subNodeIndex + 1); // 优先找兄弟节点合并,如果都不满足从左兄弟节点偷 if (thisLeftBrotherNode.isTwoKey()) { leftNode = thisLeftBrotherNode; rightNode = this; transferType = 1; parentKeyIndex = subNodeIndex - 1; } else if (thisRightBrotherNode.isTwoKey()) { leftNode = this; rightNode = thisRightBrotherNode; transferType = 2; parentKeyIndex = subNodeIndex; } else { leftNode = thisLeftBrotherNode; rightNode = this; transferType = 4; parentKeyIndex = subNodeIndex - 1; } } if (transferType == 1 || transferType == 2) { // 父节点是2节点, 降层, 这种情况下只会出现在: 根节点是2节点的时候 if (this.parent.isTwoKey()) { LOG.info("transfer :" + transferType + ", parent is two node"); this.parent.addToFirstKey(leftNode.getFirstKey()); this.parent.addToLastKey(rightNode.getFirstKey()); this.parent.clearSubNodes(); // 如果此节点有子节点,那么他的兄弟节点肯定有子节点,2-3-4的性质决定的 if (leftNode.subNodeSize() > 0) { this.parent.connectNodes(leftNode.subNodes); this.parent.connectNodes(rightNode.subNodes); } } else { LOG.info("transfer :" + transferType + ", parent is not two node"); // 不降层, 把父节点的一个key给拉下来,例如把父节点从4节点变3节点或者父节点从3节点变2节点 // 把此节点变成一个4节点(自己,兄弟,父亲的一个key),所以是4节点 // 1. 获取父节点需要被拉下来的那个key DataItem parentDataItem = this.parent.getKey(parentKeyIndex); // 删除这个父节点的key this.parent.removeKey(parentKeyIndex); // 2. 删除父节点被拉下来的key对应的subNodes, 需要删除2次, // 也就是leftNode, rightNode // 这里需要连续调用2次,list的一个属性 this.parent.removeSubNode(parentKeyIndex); this.parent.removeSubNode(parentKeyIndex); // 或者用如下的这段代码去删除这2个subNode // this.parent.removeSubNode(leftNode); // this.parent.removeSubNode(rightNode); // 3. 产生一个新的节点 Node newNode = new Node(parentDataItem); // newNode key 左边插入一个 newNode.addToFirstKey(leftNode.getLastKey()); // newNode key 右边插入一个 newNode.addToLastKey(rightNode.getFirstKey()); // 把原来的左右节点的 subNodes 给添加到新节点上去 newNode.connectNodes(leftNode.subNodes); newNode.connectNodes(rightNode.subNodes); // 4. 把新产生的节点跟父节点关联起来 this.parent.addSubNode(parentKeyIndex, newNode); } } else if (transferType == 3) { LOG.info("transfer 3"); // 从右边兄弟节点偷一个值, 从右边的兄弟节点偷 // 1. 先把右节点需要被偷的元素给取出来, 并删除 DataItem rightDataItem = rightNode.getFirstKey(); rightNode.removeFirstKey(); // 2. 取parent的key值,并删除 DataItem parentDataItem = this.parent.getKey(parentKeyIndex); this.parent.removeKey(parentKeyIndex); // 3. parent的key重新赋值 this.parent.addKey(parentKeyIndex, rightDataItem); // 4. 左边的那个2节点变成3节点 leftNode.addToLastKey(parentDataItem); // 如果右边节点有字节点(左边必有子节点),把第一个子节点给删除掉,并添加到左节点的最后一个子节点 if (rightNode.subNodeSize() > 0) { Node rightSubNode = rightNode.getFirstSubNode(); rightNode.removeFirstSubNode(); leftNode.addToLastSubNode(rightSubNode); } } else { LOG.info("transfer 4"); // 从左边兄弟节点偷一个值, 从左边的兄弟节点偷 // 1. 先把右节点需要被偷的元素给取出来, 并删除 DataItem leftDataItem = leftNode.getLastKey(); leftNode.removeLastKey(); // 2. 取parent的key值,并删除 DataItem parentDataItem = this.parent.getKey(parentKeyIndex); this.parent.removeKey(parentKeyIndex); // 3. parent的key重新赋值 this.parent.addKey(parentKeyIndex, leftDataItem); // 4. 右边的那个2节点变成3节点 rightNode.addToFirstKey(parentDataItem); // 如果左边节点有子节点,把最后一个子节点给删除掉,并添加到左节点的第一个子节点 if (leftNode.subNodeSize() > 0) { Node leftSubNode = leftNode.getLastSubNode(); leftNode.removeLastSubNode(); rightNode.addToFirstSubNode(leftSubNode); } } }
转换函数(TwoThreeFourTree):
public void transfer(int key) { List<Integer> path = this.path(key); Node curNode = this.root; for (int i = 0; i < path.size(); i++) { boolean haveSub = (i != (path.size() - 1)); Node nextCurNode = null; if (haveSub) { int nextCodeIndex = path.get(i + 1); nextCurNode = curNode.getSubNode(nextCodeIndex); } if (curNode.parent != null) { curNode.transfer(); } if (haveSub) { curNode = nextCurNode; } } }
最后删除函数如下(TwoThreeFourTree):
public boolean delete(int key) { if (this.find(key) == null) { return false; } int originHeight = this.height(); // 唯一的一个 if (originHeight == 1) { if (this.root.keySize() == 1) { this.root = null; } else { this.root.removeKey(new DataItem(key)); } return true; } List<Integer> path = this.path(key); this.transfer(key); int newHeight = this.height(); // 是否因为转换而导致降层了 boolean haveReduceHeight = originHeight > newHeight; int pathStartIndex = haveReduceHeight ? 1 : 0; Node curNode = this.root; for (int i = pathStartIndex; i < path.size(); i++) { boolean haveSub = (i != (path.size() - 1)); // haveSub = !curNode.isLeaf(); Node nextCurNode = null; int nextCodeIndex = 0; if (haveSub) { nextCodeIndex = path.get(i + 1); nextCurNode = curNode.getSubNode(nextCodeIndex); } for (int j = 0; j < curNode.keySize(); j++) { DataItem keyItem = curNode.getKey(j); if (keyItem.key == key) { if (curNode.isLeaf()) { curNode.removeKey(j); return true; } else { // 替换到下一个 DataItem subDataItem = nextCurNode.getLastKey(); // 此节点和子节点调换 curNode.removeKey(j); curNode.addKey(j, subDataItem); nextCurNode.removeLastKey(); nextCurNode.addKey(nextCodeIndex, keyItem); // 跳出j的循环,继续i的循环 break; } } } if (haveSub) { curNode = nextCurNode; } } return true; }



