博客作业03--栈和队列
1.学习总结
1.1知识总结
逻辑结构包括:集合,线性结构,树形结构,图形结构
线性结构包括:线性表,链表,栈,队列,串
树形结构包括:二叉树等
栈是一种后进先出表,有顺序存储结构和链式存储结构,基本操作包括:初始化、销毁、进栈、出栈、判断栈空、去栈顶。主要应用有:前缀表达式转后缀表达式以及后缀表达式的计算、迷宫问题
队列是一种先进先出表,有循序存储结构、循环结构、链式结构,基本操作有:初始化、销毁、进队、出队、判断队空。循环结构中判断元素个数为 (rear-front+max)%max,出队时rear=(rear+1)%max,进队时front=(front+1)%max,队满(rear+1)%max=front;链式存储结构中,有两种节点:链队节点、数据节点
1.2思维导图

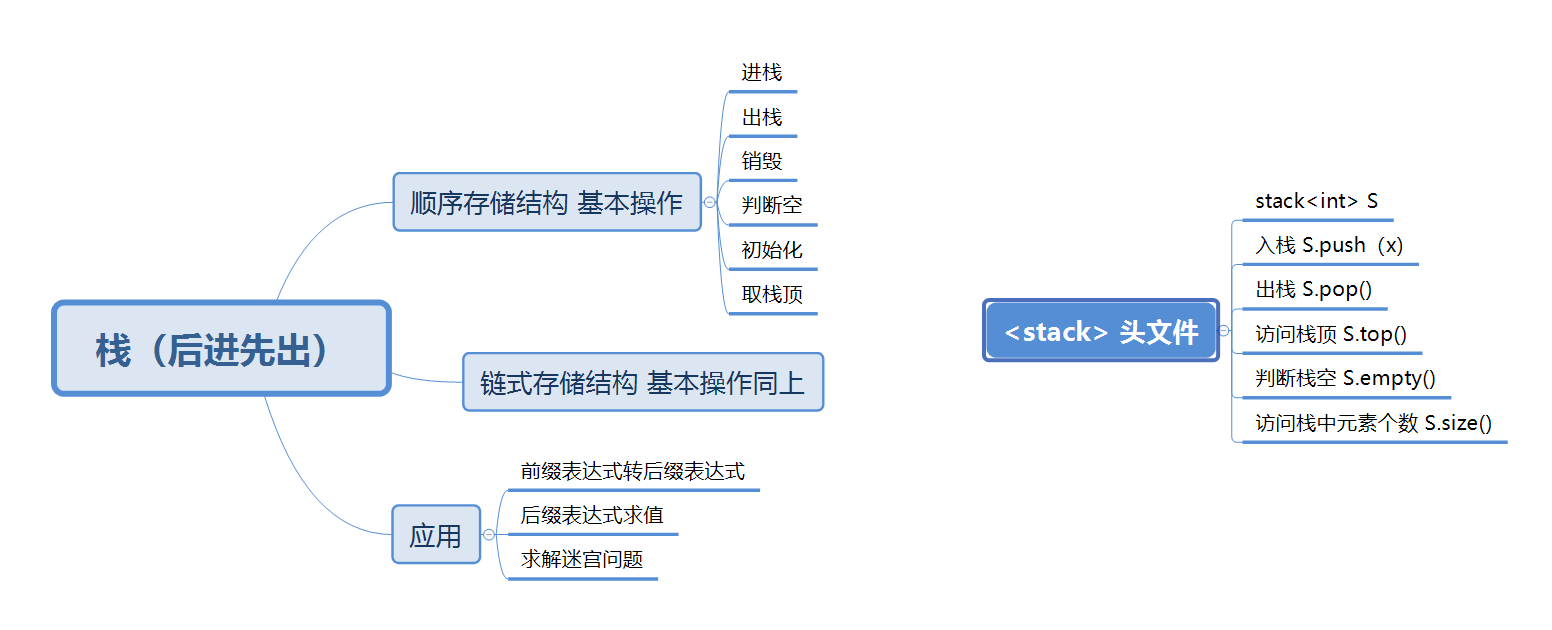
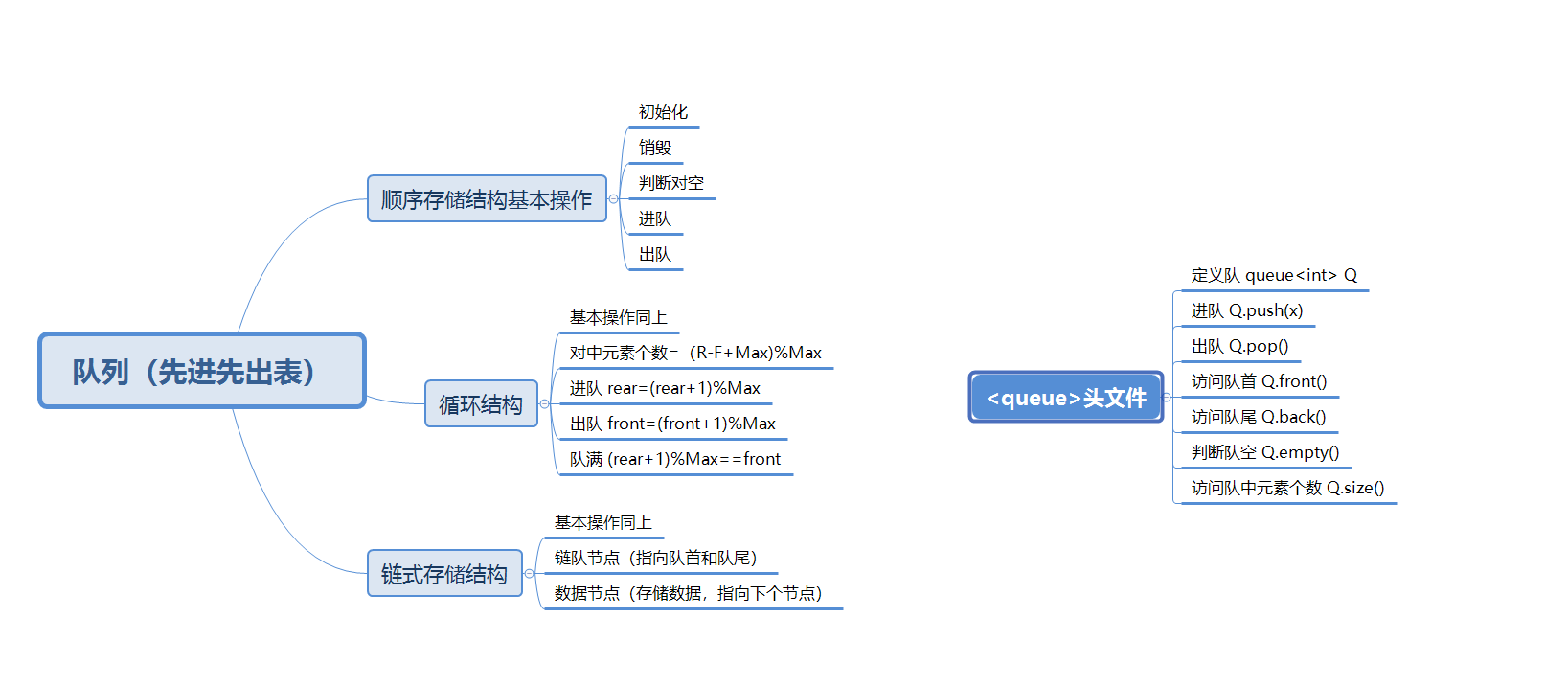

2.PTA实验作业
题目1:字符串是否对称
设计思路
输入一串字符串;
将每个字符入栈;
再全部出栈,存在字符数组中;
对比连个字符数组是否相同 ;
代码截图
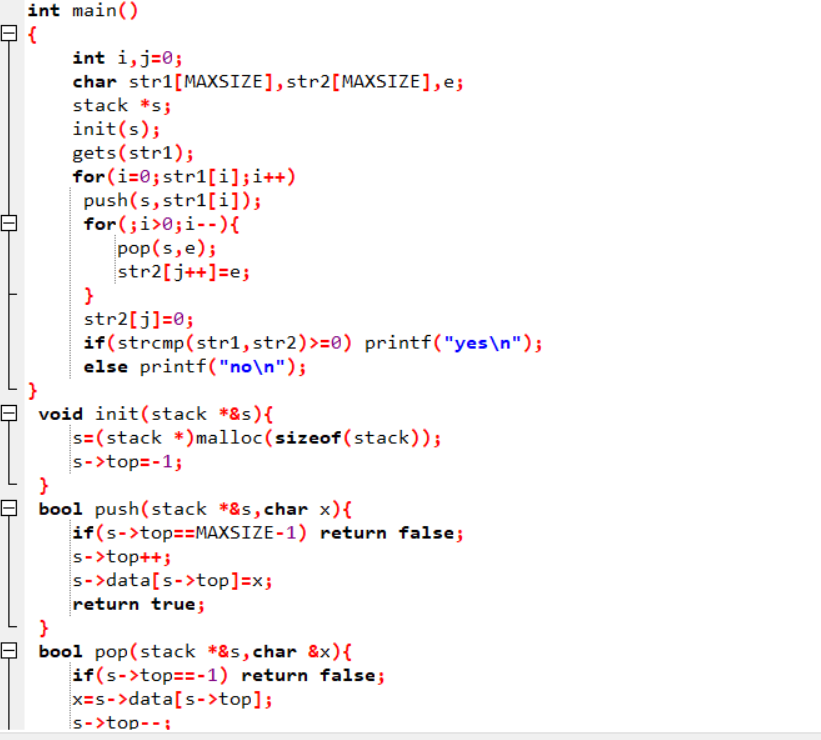
PTA提交列表说明

错误说明:

出栈的字符串数组最后没有加结束符,导致对称时答案错误
题目2:报数游戏
设计思路
定义队列Q,让1到n的数进队
i=0
while(i<n){
j=0;
while(j<m&&队不为空){
前m个数从队首出队,并进队到队尾
}
第m个元素为报数的元素,直接出队,并输出
}
代码截图
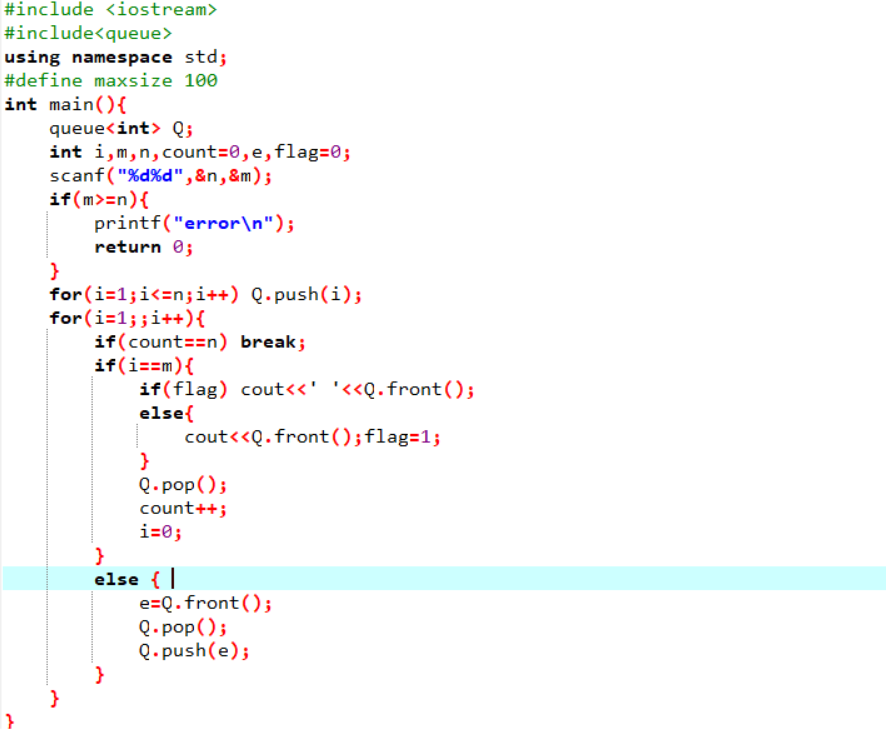
PTA提交列表说明
本题最开始不是用

题目3:银行排队问题之单队列多窗口服务
设计思路
typedef struct{
float T,P;
}person; //存放顾客信息
typedef struct{
person data[maxsize];
int front,rear;
}Queue; //顾客队列
typedef struct{
int state; //窗口状态,是否空闲
float overtime; //结束时间
int Ptime; //窗口处理次数
float waittime; //顾客在本窗口的等候花时间
}window; //窗口信息
输入每个顾客的信息,若有顾客处理时间超过60分钟,则修改为60
每个顾客的数据入队
while(队不为空){
出队
for i=0 to k{
判断窗口是否空闲{
若有,则进行处理,并记下该窗口结束的时间,同时处理次数加1
若没有,记下在该窗口的等待时间
若等待时间<=0,则在该窗口处理,改变窗口结束时间以及处理次数
}
若窗口全部有人{
从窗口中找出最小等待时间的窗口,并改变该窗口的结束时间以及处理次数;
将等待时间加入总等待时间
从每次的最小等到时间中找出最长的等待时间
}
}
所有顾客都判断结束,计算平均等待时间,在窗口中找出最后完成的时间
代码截图
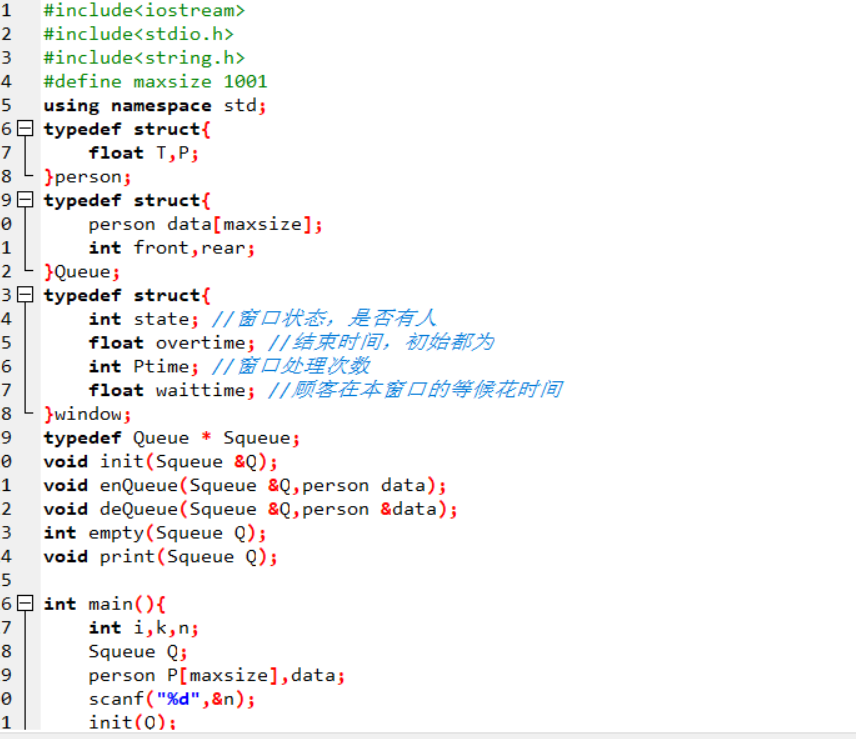
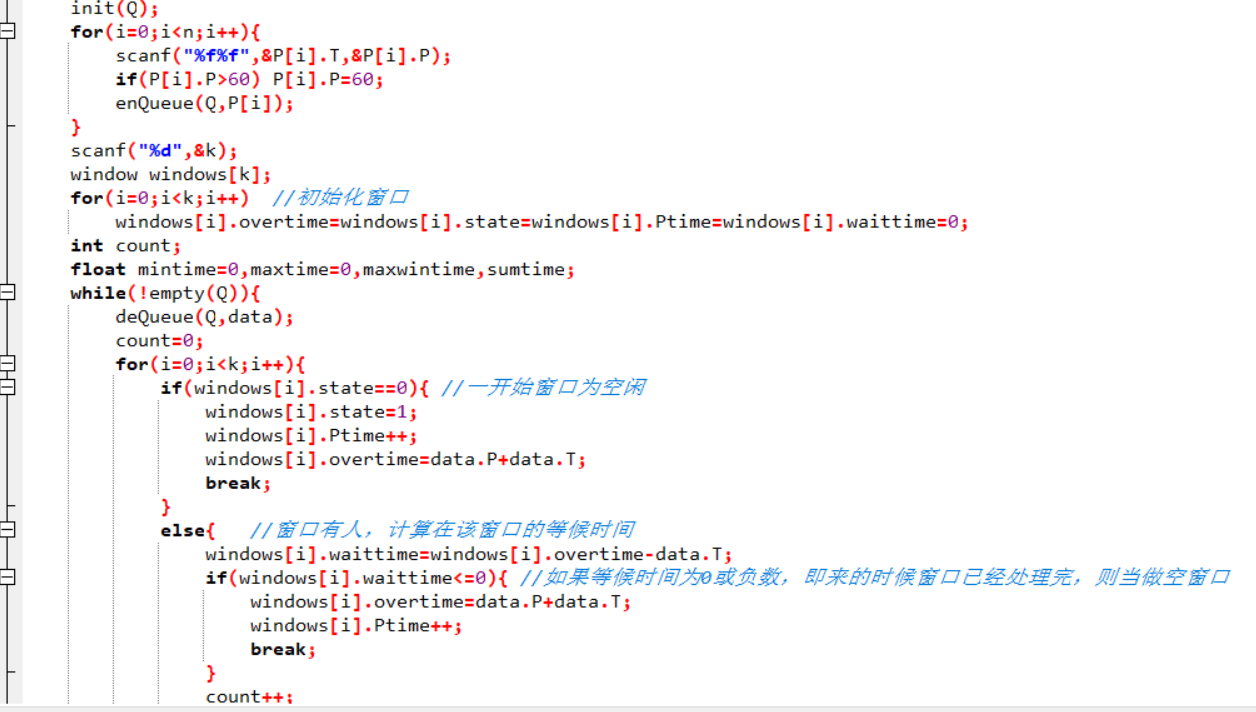

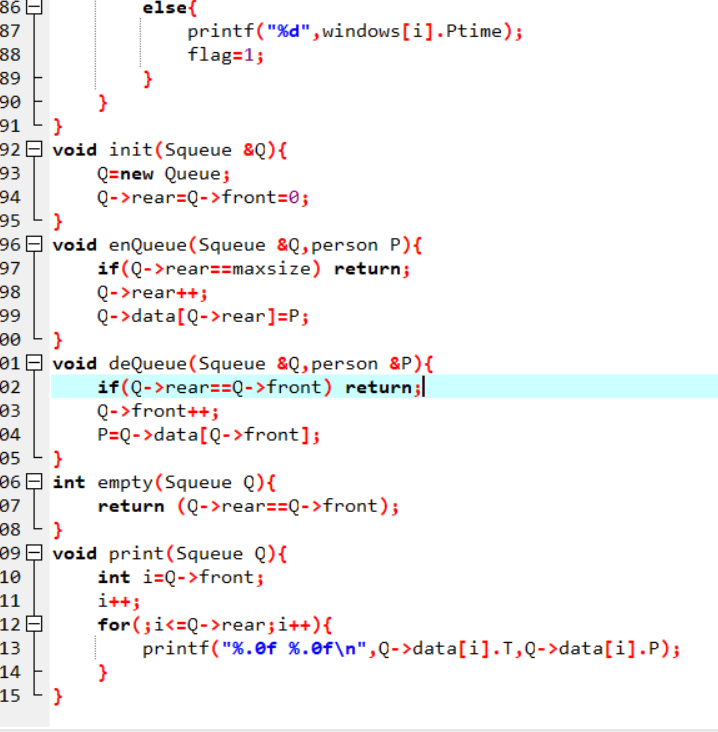
PTA提交列表说明

本题的主要问题是时间的数据类型要为浮点型,一开始定义为整数型,导致一直有的点过不了
3.截图本周题目集的PTA最后排名
栈PTA排名
队列PTA排名

我的总分
总分:227
4. 阅读代码
铁轨问题:
某城市有一个火车站,铁轨铺设如图所示。有n节车厢从A方向驶入车站,按进站顺序编号为1~n。你的任务是让它们按照某种特定的顺序进入B方向的铁轨并驶出车站。为了重组车厢,你可以借助中转站C。这是一个可以停放任意多节车厢的车站,但由于末端封顶,驶入C的车厢必须按照相反的顺序驶出C。
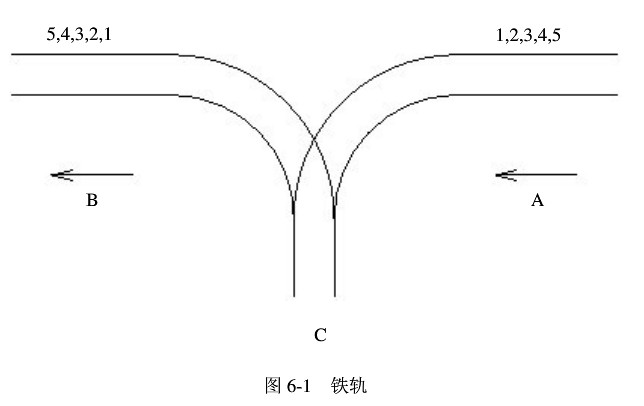
代码:
#include<cstdio>
#include<stack>
#include<iostream>
using namespace std;
const int MAXN =1000+10;
int n,target[MAXN];
int main()
{
while(scanf("%d",&n)==1){
stack<int> s;
int A=1,B=1;
for(int i=1;i<=n;i++)
scanf("%d",&target[i]);
int ok=1;
while(B<=n){
if(A==target[B]) {A++;B++;}
else if(!s.empty()&&s.top()==target[B]) {s.pop() ;B++;}
else if(A<n) {s.push(target[B];A++;}
else {ok=0;break;}
}
printf("%s\n",ok?"Yes":"No");
}
return 0;
}
本题中对于每个车厢,一旦从A移入C,就不能再回到A了;一旦从C移入B,就不能回到C了。换句话说,在任意时刻,只有两种选择:A–>C和C–>B。
5. 代码Git提交记录截图