3、深度学习入门之数值微分P94、P95、P96、P97、P98

$f'(x) = \lim_{{\Delta x \to 0}} \frac{f(x0+\Delta x) - f(x0)}{\Delta x}$

$f(x0+\Delta x) - f(x0) = \Delta y$

$f'(x) = \lim_{{\Delta x \to 0}} \frac{\Delta y}{\Delta x}$

$f'(x)$就是导数

导数粗糙的理解为就是在某点的切线斜率

可导意味着在某点处它的导数存在

 

微分：

$y=f(x) = 3x,             x0->(x0+\Deltax)$

$\Delta y = f(x0+ \Delta x) - f(x0) = 3(x0 + \Delta x) -3x0 = 3\Delta x$

 

 

 

$y = f(x) = x^2 $

$\Delta y = (x0+\Delta x)^2 - (x0)^2 = 2(x0)^2\Delta x + (\Delta x)^2$

如果满足$\Delta x -> 0, \Delay y = A \Delta x + o(\Deltax)$，此时称这个函数在这一点可微。 

 

$f(x0+\Delta x) - f(x0) = A\Delta x + o(\Delta x)$

$(f(x0+\Delta x) - f(x0)) / \Delta x = A + o(\Delta x) / \Delta x $

 

 

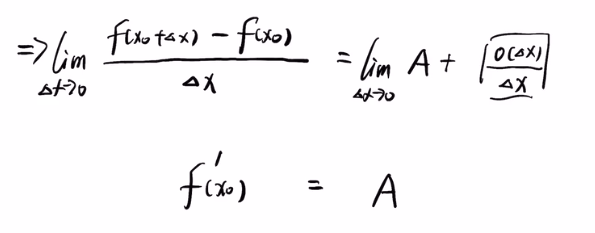
https://www.bilibili.com/video/BV1bW4y1j77v/

 

 

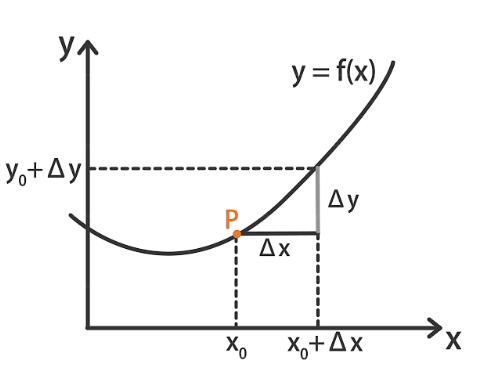
$y = f(x)$，　　

$\Delta y = f(x_0 + \Delta x) - f(x_0)$

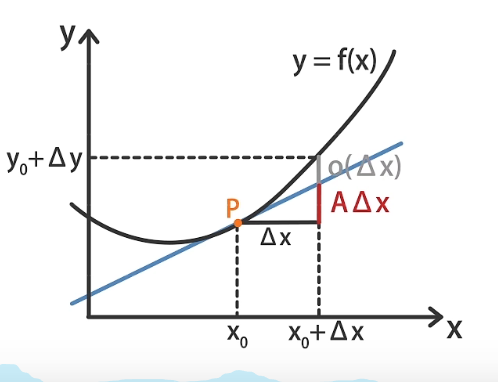
 设红色为$A\Delta x$,灰色为$o \Delta x$,那么下面会得到：$\Delta y =A\Delta x + o \Delta x$

将$\Delta x$称为自变量的微分，记作$dx$

$dx = \Delta x$

将$A\Delta x$称为函数 $x0$相对于自变量增量$\Delta x$的微分，也就是函数值的微分，记作$dy$

$dy = A\Delta x$

$dy + o \Delta x = \Delta y$

$dy = A(dx)$ 

A就是导数了，也就是函数在某点的变化率

$f'(x)$是导数

$dy = f'(x) dx$

$f'(x)=\frac{dy}{dx}$

 

 

https://www.bilibili.com/video/BV1PL411W7Mu/

 https://www.bilibili.com/video/BV1Ja411x7fB/

https://www.bilibili.com/video/BV1sp4y1Y7uz/