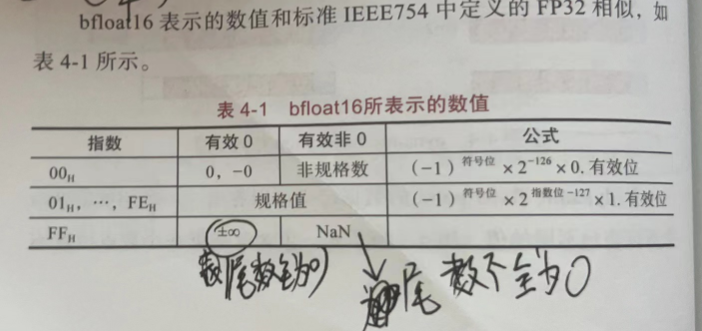
3、运算精度的选择(P106、P107、P108、P109、P110、P111)

1、fp16和fp32有什么区别？

FP32（单精度浮点数）和FP16（半精度浮点数）是两种不同的浮点数表示方式，它们在精度和存储空间上有显著的区别。下面是它们的主要区别以及一个示例来说明这些区别：

1. 精度：

   • FP32：单精度浮点数使用32位来表示一个数，其中包括1位符号位、8位指数位和23位尾数位。它具有较高的精度，通常用于大多数科学计算和图形渲染任务。
   • FP16：半精度浮点数使用16位来表示一个数，其中包括1位符号位、5位指数位和10位尾数位。它具有较低的精度，通常用于需要较小存储空间和更快计算速度的应用，如深度学习模型训练。

2. 存储空间：

   • FP32：由于其较长的位数，FP32需要更多的存储空间来表示相同范围的数字。每个单精度浮点数占用4字节（32位）的存储空间。
   • FP16：半精度浮点数使用较少的位数，因此它们需要更少的存储空间。每个半精度浮点数占用2字节（16位）的存储空间。

示例：

假设我们有一个表示圆的半径的浮点数。如果我们想要使用FP32表示，可以使用以下形式：

• 半径为1.5的圆的FP32表示为：1.5

如果我们要使用FP16表示，同样的圆的表示形式将会是：

• 半径为1.5的圆的FP16表示：1.5

虽然这两个表示都可以表示1.5这个数，但它们在存储空间上有所不同。FP32版本需要4个字节，而FP16版本只需要2个字节。这对于需要大量存储和传输浮点数的应用来说可能是重要的考虑因素。

然而，需要注意的是，FP16的精度相对较低，因此在某些情况下，它可能会导致数值不稳定或精度损失。在深度学习中，使用FP16可以加速训练过程，但需要谨慎处理数值稳定性的问题。在科学计算等需要高精度的领域，通常会使用FP32或更高精度的浮点数表示。

2、32位浮点基准：

我理解的是在测试中，32位浮点数执行某个特定任务或计算时，成功率为99.1%。

3、浮点数和整型数所能表示的精度相差很大。怎么理解？

浮点数和整数数值在表示精度上的差异主要体现在它们处理小数部分的能力上。浮点数可以表示小数部分，而整数只能表示整数部分。这意味着浮点数可以表示范围更广、精度更高的数值，但在某些情况下可能会引入舍入误差。

下面通过一个例子来更好地理解这个概念：

考虑计算圆的面积，其中半径为3.5。首先，我们来看整数表示：

整数表示：

• 半径：3（整数部分）
• 面积计算：面积 = π × 半径 × 半径 = π × 3 × 3 = 28.27（近似值）

在整数表示中，我们只能表示半径的整数部分，所以半径被截断为3，这导致了面积的近似计算。

现在，我们来看浮点数表示：

浮点数表示：

• 半径：3.5（包括小数部分）
• 面积计算：面积 = π × 半径 × 半径 = π × 3.5 × 3.5 = 38.48（近似值）

在浮点数表示中，我们可以保留半径的小数部分，因此计算得到的面积更接近精确值。

这个例子说明了浮点数的主要优势：它们能够表示小数部分，因此在某些情况下具有更高的精度。但需要注意的是，浮点数的精度仍然有限，可能会引入舍入误差。因此，在某些高精度计算或需要精确性的应用中，可能需要谨慎处理浮点数的精度问题，或者考虑使用高精度的数值表示方式。整数则更适合表示不需要小数部分的数值，如计数、索引等。

4、怎么理解指数位和尾数位？

指数位和尾数位可以用二进制来表示浮点数的大小和精度。例如，13.25可以用科学计数法写成1.325×10¹，那么指数位就是1，尾数位就是1.325。在计算机中，指数位和尾数位都用二进制来存储，例如float类型有8位指数位和23位尾数位，那么13.25可以用下面的二进制来表示：

符号位	指数位	尾数位
0	10000010	10101000000000000000000

13.25的二进制表示是：1101.01

接下来，规范化这个二进制数，将小数点移到最左边，然后用科学计数法表示：

1101.01 => 1.10101 * 2³

现在，我们可以将这个数表示为IEEE 754单精度浮点数的格式：

• 符号位：0（因为13.25是正数）
• 指数位：指数位是3，但要加上偏移值127（IEEE 754单精度的偏移值），所以指数位为130的二进制表示为10000010。
• 尾数位：尾数部分是1.10101000000000000000000(取小数点后面的数)，需要舍入到23位。所以尾数位为10101000000000000000000。

将这些部分组合在一起，得到13.25的IEEE 754单精度浮点数表示：

01000001010101000000000000000000

5、什么是乘法阵列？

6、乘法阵列中的乘法器是什么？

7、怎么根据fp32的二进制转成十进制

根据fp32的二进制转成十进制，需要先了解fp32的格式和规则。fp32是单精度浮点数，占用32位，其中1位是符号位，8位是指数位，23位是尾数位。符号位表示正负，指数位表示2的幂次，尾数位表示有效数字。具体的转换步骤如下：

1. 根据符号位确定正负，0为正，1为负。
2. 根据指数位计算2的幂次，指数位的值减去127得到实际的幂次。
3. 根据尾数位计算有效数字，尾数位的值加上一个隐含的1，然后乘以2的幂次得到有效数字。
4. 将符号、有效数字和小数点组合起来得到十进制数。

例如，将01000000100100000000000000000000转成十进制：

1. 符号位为0，表示正数。
2. 指数位为10000001，表示129，减去127得到2，表示2的2次方。
3. 尾数位为00100000000000000000000，表示0.125(0*2^-1+0*2^-2+1*2^-3+0)，加上隐含的1得到1.125，乘以2的2次方得到4.5。
4. 组合起来得到正4.5。

8、bfloat16怎么根据二进制转成十进制？