9、5.3非确定有限自动机
- 定义：一个非确定有限自动机(Nondeterministic Finite Automata，NFA)M是一个五元式M=(S, Σ, f, S0, F)，其中：
-
- 1. S: 有穷状态集
-
- 2. Σ ：输入字母表(有穷)
-
- 3. f: 状态转换函数，为S×Σ* → 2 S的部分映射
-
- 4. S 0 ⊆S是非空的初态集
-
- 5. F ⊆S ：终态集(可空)
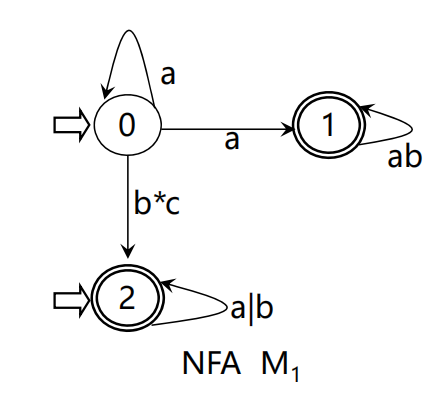
- 从状态图看NFA 和DFA的区别
-
- NFA可以有多个初态
- 弧上的标记可以是Σ*中的一个字(甚至可以是一个正规式)，而不一定是单个字符
- （正规式可以理解为：识别正规式所对应的正规集中间的一个字）
- 同一个字可能出现在同状态射出的多条弧上（表示0-1可以为a,0-0也可以是a）
-
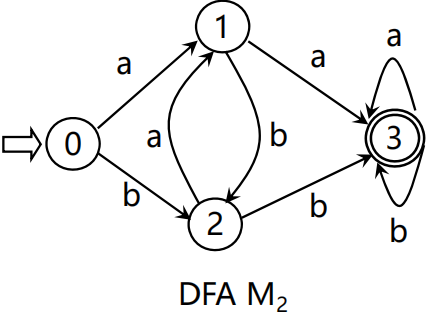
DFA是NFA的特例
- 对于Σ*中的任何字α，若存在一条从初态到某一终态的道路，且这条路上所有弧上的标记字连接成的字等于α (忽略那些标记为ε的弧)，则称α为NFA M所识别(接收)
- NFA M所识别的字的全体记为L(M)
-
定义：对于任何两个有限自动机M 和M’，如果L(M)=L(M’)，则称M 与M’等价
-
自动机理论中一个重要的结论：判定两个自动机等价性的算法是存在的
- DFA与NFA识别能力相同!
-
对于每个NFA M存在一个DFA M’，使得L(M)=L(M’)
-
