3、3.3语法树与二义性

1、推导和语法树

最左推导和最右推导

• 从一个句型到另一个句型的推导往往不唯一

　　　　E+E⇒i+E⇒i+i

　　　　E+E⇒E+i⇒i+i

• 最左推导：任何一步α⇒β都是对α中的最左非终结符进行替换
• 最右推导：任何一步α⇒β都是对α中的最右非终结符进行替换

语法树

• 用一张图表示一个句型的推导，称为语法树
• 一颗语法树是不同推导过程的共性抽象

　　　G(E): E→i | E+E | E*E | (E)

　　　(i*i +i）

 

 

 

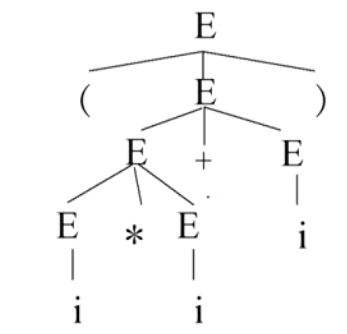
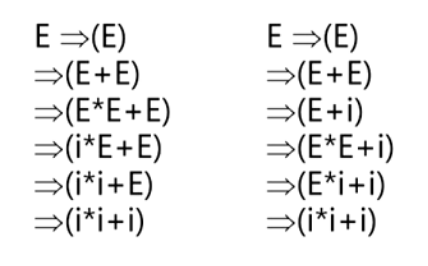
 (两种不同的推导过程，等到同一棵语法树)(可以理解为两种不同的最左推导)（这种形式也可以证明是二义的）

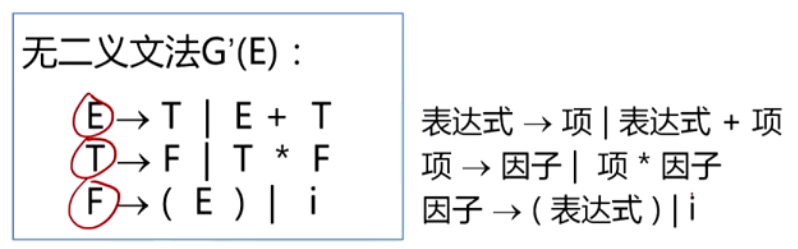
 2、语法树与二义性

一个句子是否只对应唯一一颗语法树？

(i*i+i)对于这个文法会产生下面两种语法树

 

 

 

 

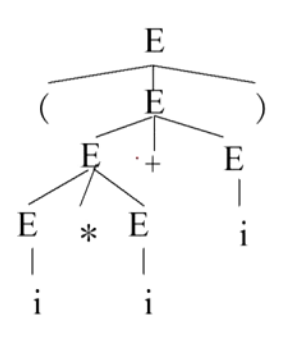
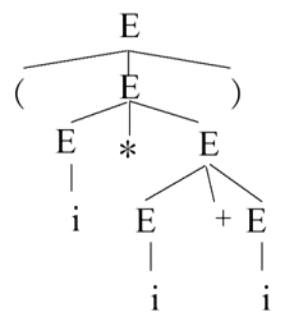
•  对每一个句型，该句型一定有一个推导过程（可能不唯一），推导过程一定对应一颗语法树（推导过程可能不唯一，当然语法树也可能不唯一。
• 文法的二义性，如果一个文法存在某个句子或句型对应两颗不同的语法树，则说这个文法是二义的。

　　　　G(E)：E→i|E+E|E*E|(E)是二义文法

• 语言的二义性：一个语言是二义的，如果对它不存在无二义的文法

　　　对于语言L，可能存在G和G‘，使得L（G）=L（G’）=L，有可能其中一个文法为二义的，另一个为无二义的。

 语言的二义性

 

 

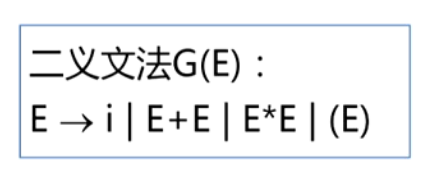
• 考虑句子(i*i+i)

 

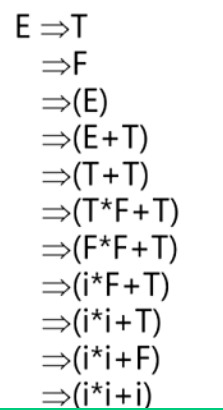
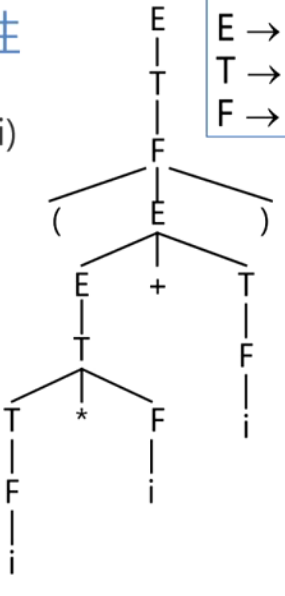
• 二义性问题是不可判定问题，即不存在一个算法，它能在有限的步骤内，确切的判定一个文法是否是二义的。

•  可以找到一组无二义文法的充分条件(也就是说可以列出一组条件，如果一个文法满足这些条件的话，我们就能断定它是无二义的。但是不满足的话，可能是二义的也不能是无二义的)