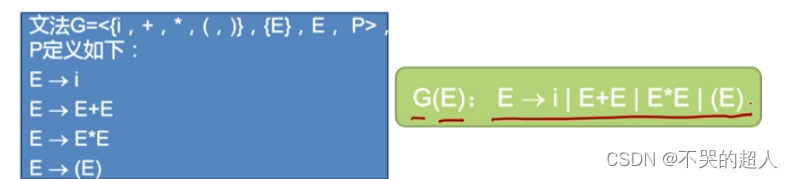
1、3.1上下文无关文法
1、文法
2、语言描述的几个基本概念
基本概念1
字母表:一个有穷字符集,记为∑
字母表中的每个元素称为字符
∑上的字(也叫字符串)是指由∑中的字符所构成的一个有穷序列
不包含任何字符的序列称为空字,记为ε
用∑* 表示∑上所有字的全体,包含空字ε
例如:设∑={a, b}, 则
∑*={ε, a, b, aa, ab, ba, bb,…}
基本概念2
- ∑*的子集U和V的连接(积)定义为
- UV = {α,β | α∈U&β∈V}(U和V的前后顺序影响结果)
示例:设
U={a, aa}
V={b, bb}
UV={ab,abb,aab,aabb}
- V自身的n次积记为
Vn = VVVVV…(n个)
- V0 = {ε}
- V*是V的闭包:V* = V0∪V1∪V2∪V3∪V4∪…
- V+是V的正规闭包:V+ = VV*
- 思考一下V*和V+的区别?
有时是相等,有时不相等。
如果V中原来没有空字,闭包会有空字,正规闭包不会有空字。
- 设U={a, aa}
U* = {ε,a, aa, aaa, aaaa, aaaaa,…}
U+ ={a, aa, aaa, aaaa,…}
3、上下文无关文法
https://blog.csdn.net/panjunbiao/article/details/9268891
https://blog.csdn.net/chenxu6/article/details/46490689
文法描述形式
上下文无关文法G是一个四元组G=(VT, VN, S, P),其中:
- VT:终结符(Terminal)集合(非空)(不可以分解)
- VN: 非终结符集合(非空),且VT∩VN=Ø(可以分解)
- S:文法的开始符号,S∈VN
- P:产生式集合(有限),每个产生式形式为
P→α,P∈VN,α∈(VT∪VN)*(→理解为代替为)
- 开始符S至少必须在某个产生式的左部出现一次,否则就没有意义
巴科斯范式(BNF)
- “→"用”::="表示
- 约定
P→α1
P→α2
…
P→αn
可以缩写为
P→α1|α2|…|αn
其中,"|“读成"或”,称αi为P的一个候选式
表示一个文法时,通常只给出开始符号和产生式,就可以了。
非终结符用大写字母表示,终结符用小写字母表示