EM算法

概率模型有时含有观测变量，又含有隐变量或潜在变量。如果概率模型的变量都是观测变量，那么给定数据，可以直接用极大似然估计法，或贝叶斯估计法估计模型参数。但是，当模型含有隐变量时，就不能简单地使用这些简单方法，EM算法就是含有隐变量的概率模型参数的极大似然估计法，极大后验概率估计法。

EM算法首先选取参数的初值，记作 \(\theta^(0) = (\pi^{(0)}, p^{(0)}, q^{(0)})\), 然后通过下面的步骤迭代计算参数的估计值， 直至收敛为止。第\(i\)次迭代参数的估计值为\(\theta^(i) = (\pi^{(0)}, p^{(0)}, q^{(0)})\)
E步： 计算在模型参数\(\pi^{(i)}, p^{(i)}, q^{(i)}\)下观测数据\(y_j\)来自掷硬币B的概率

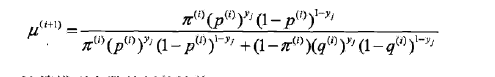
M步： 计算模型参数的新估计值

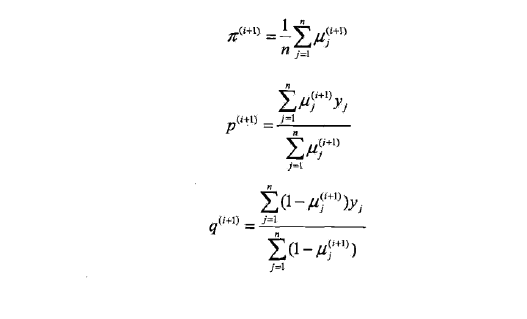
关于步骤（1）参数的初值可以任意选择，但需注意EM算法对初值是敏感的
关于步骤（2）E步求Q，Q函数中的Z是为未观测数据，Y是观测数据。注意\(Q(\theta, \theta^{(i)})\)中的第一个变量时要极大化的参数，第二个变量表示参数的当前估计值，每次迭代实际在求Q函数及其极大。
步骤（4）给出停止迭代的条件，一般是对较小的正数\(\varepsilon_1, \varepsilon_2\), 若满足

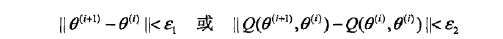
则停止迭代。