文本主题模型--LDA

隐含狄利克雷分布（Latent Dirichlet Allocation ,简称LDA)

• 贝叶斯模型
  贝叶斯模型主要涉及“先验分布”， “数据（似然）”和“后验分布”三块，在贝叶斯学派中：
                     先验分布 + 数据（似然）= 后验分布
  可以理解为通过在现先验分布的基础上更新后验分布
• 二项分布与Beta分布
  二项分布是n重伯努利试验成功次数的离散概率分布。如果试验E是一个n重伯努利试验，每次伯努利试验的成功概率为p, x代表成功的概率分布是二项分布，记为X~B(n, p)
                      $B(k |n, p) = {n \choose k}p^k(1-p)^{n-k}$
  其中p为成功的概率，k为成功的次数， n为试验的总次数。
  共轭分布(conjugate distribution)：如果由先验分布和似然分布所确定的后验分布与该先验分布属于同一种类型的分布，则该先验分布为似然分布的共轭分布，也称为共轭先验
  Beta分布：可以看作一个概率的概率分布，当不知道一个东西的具体概率是多少时，它可以给出所有概率出现的可能性大小。Beta分布是一个连续分布，由于它描述概率p的分布，因此其取值范围为0~1
                         $Beta(p|\alpha, \beta) = \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)}p^{\alpha-1}(1-p)^{{\beta-1}}$
                      其$\Gamma$函数，满足$\Gamma(x)=(x-1)!$
• 多项式分布与DirichLet分布
  多项式分布和Dirichlet分布分别为高维的多项式分布和Beta分布
  多项式分布：
           $multi(m_1,m_2,m_3|n,p_1,p_2,p_3) = \frac{n!}{m_1! m_2!m_3!}p_1^{m_1}p_2^{m_2}p_3^{m_3}$
  Dirichlet分布：
            $Dirichlet(p_1,p_2,p_3|\alpha_1,\alpha_2, \alpha_3) = \frac{\Gamma(\alpha_1+ \alpha_2 + \alpha_3)}{\Gamma(\alpha_1)\Gamma(\alpha_2)\Gamma(\alpha_3)}p_1^{\alpha_1-1}(p_2)^{\alpha_2-1}(p_3)^{\alpha_3-1}$
• LDA主题模型
  假设我们有M篇文档，对应第d个文档有$N_d$个词，即输入为如下图：
                       
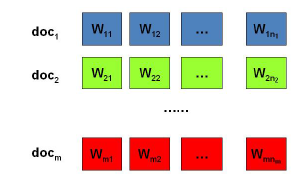
  目标为找出每一篇文档的主题分布和每一个主题中词的分布
  LDA假设文档主题的先验分布是Dirichlet分布，即对于任一文档d, 其主题分布$\theta_d$
                                     $\theta_d = Dirichlet(\vec \alpha)$
  其中，$\alpha$为分布的超参数，是一个K维向量
  LDA假设主题中词的先验分布是Dirichlet分布，即对于任一主题k,其词分布$\Beta_k$为：
                                     $\Beta_k = Dirichlet(\vec \eta$
  其中， $\eta$为分布的超参数，是V维向量。V代表词汇表 里所有词的个数
                 
  
  
  
  
  参考：
  https://www.cnblogs.com/pinard/p/6831308.html