算法笔记(6)数列分块
原发表于我的博客
前言
分块不能说是一种数据结构,它是一种思想,无论是数列分块,块状链表,还是数论分块,莫队算法,都应用了分块的思想。
本文主要介绍狭义上的分块,即数列分块。
数列分块的引入
数列分块可以说是暴力,一种优美的暴力,它的基本思路是,把数列分成若干块(一般取\(\sqrt n\)),分块预处理。
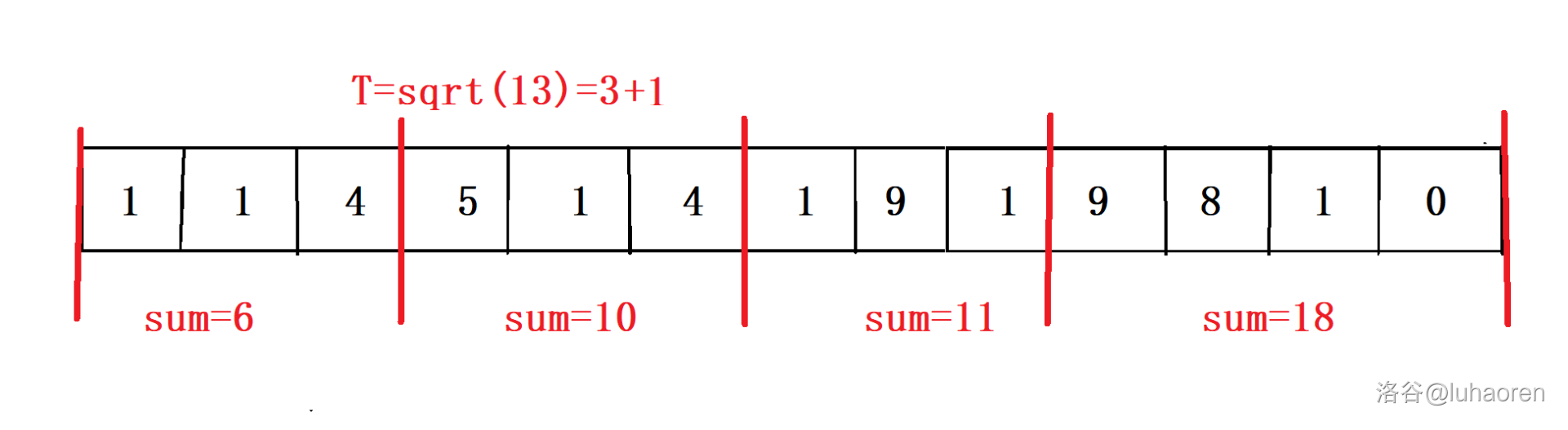
在修改时,块内直接修改标记(别告诉我你不会线段树),块外暴力修改(同时更新数据)
同理,查询时块内直接看预处理的数据和标记,块外(边角料)暴力。
数列分块的复杂度是\(O(n\sqrt n)\),肯定比线段树或树状数组的\(O(n\log n)\)要慢,但是它容易写,而且直观,可以解决一些线段树无法维护的问题,在复杂度允许的情况下可以使用。
数列分块复杂度证明(可跳过)
设对数列分成\(T\)块。
最坏情况下需要修改\(S_1< T\)块。
块外最坏情况下需要修改\(S_2<\frac{2n}{T}\)个元素。
整体操作\(\le S_1+S_2\)次。
由均值不等式,
即
故数列分块单次操作最坏情况下小于
忽略常数,则数列分块总体复杂度为
若\(q\),\(n\)同阶,则时间复杂度为
注:刚学均值不等式没几天,证明的可能不对,如果有错误请评论或私信我指出。
代码详解
以loj. 数列分块入门1为例。
预处理
在预处理中,会处理以下几个变量。
R,L代表每一个块的左右边界(其实可以不处理这个,但是写起来比较麻烦)
pos保存着每一个数所在的块。
int t=sqrt(n);//分t个块
for(int i=1;i<=t;i++) L[i]=(i-1)*t+1,R[i]=i*t;//处理出每个块的左右边界
if(R[t]<n) t++,L[t]=R[t-1]+1,R[t]=n;//分块后最后一部分很可能不在块内,所以要增加一个块
for(int i=1;i<=t;i++)
for(int j=L[i];j<=R[i];j++) pos[j]=i;//处理出每个数所在块的编号
注意,分块后最后一部分很可能不在块内,所以要增加一个块。
这个预处理的时间复杂度为\(O(n)\)。
修改
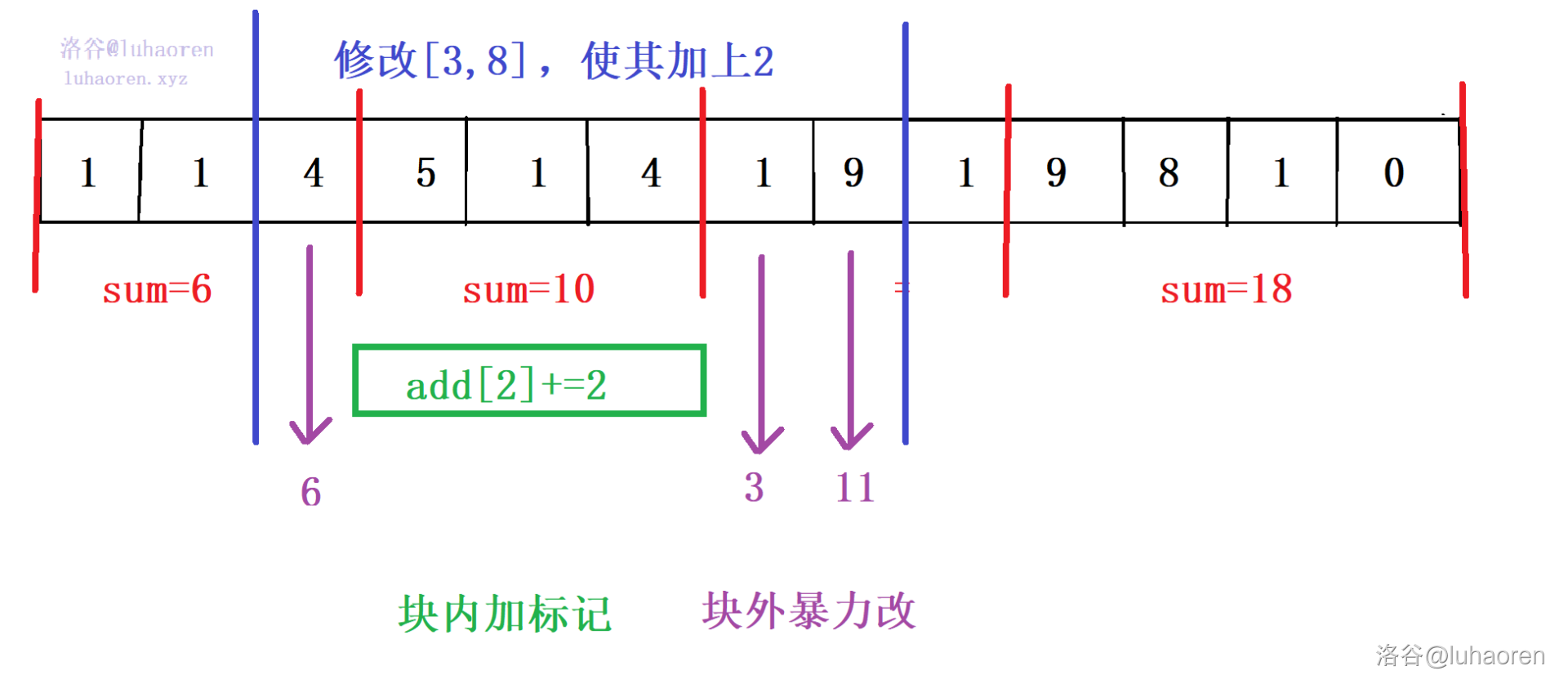
修改操作采用的是”块内修改标记,块外暴力修改“的策略。
void change(int l,int r,int k){
int p=pos[l],q=pos[r];//找到左右边界所在的块
if(p==q){
//如果这个区间在一个块内,就直接暴力修改
for(int i=l;i<=r;i++) a[i]+=k;
}
else{
for(int i=l;i<=R[p];i++) a[i]+=k;//整块左边的”边角料“,暴力修改
for(int i=p+1;i<=q-1;i++) add[i]+=k;//对于整块,直接修改标记
for(int i=L[q];i<=r;i++) a[i]+=k;//整块右边的”边角料“
}
}
这就是分块的基本操作,接下来看几道例题。
例题
数列分块入门 2
最开始看到这题,我以为是树套树,后来老师讲解才发现,分块真™暴力。
题意:区间加法,询问区间内小于某个值\(x\)的元素个数。
分析:这题看起来很难,实际上直接查询操作直接暴力枚举即可。
AC代码
#include<bits/stdc++.h>
using namespace std;
const int N=5e4+10;
int a[N],L[N],R[N],add[N],pos[N];
int n;
void change(int l,int r,int k){
int p=pos[l],q=pos[r];
if(p==q){
for(int i=l;i<=r;i++) a[i]+=k;
}
else{
for(int i=l;i<=R[p];i++) a[i]+=k;
for(int i=p+1;i<=q-1;i++) add[i]+=k;
for(int i=L[q];i<=r;i++) a[i]+=k;
}
}
int query(int l,int r,int k){
int cnt=0;
for(int i=l;i<=r;i++){
if(a[i]+add[pos[i]]<k*k) cnt++;
}
return cnt;
}
int main(){
cin>>n;
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
int t=sqrt(n);
for(int i=1;i<=t;i++) L[i]=(i-1)*t+1,R[i]=i*t;
if(R[t]<n) t++,L[t]=R[t-1]+1,R[t]=n;
for(int i=1;i<=t;i++)
for(int j=L[i];j<=R[i];j++) pos[j]=i;
for(int i=1;i<=n;i++){
int opt,l,r,k;
scanf("%d%d%d%d",&opt,&l,&r,&k);
if(opt) printf("%d\n",query(l,r,k));
else change(l,r,k);
}
}
数列分块入门 3
题意:区间加法,询问区间内小于某个值\(x\)的前驱(比其小的最大元素)。
分析:
考虑每个块建一个vector,块内排序,每次散块修改就重构,复杂度大概是预处理\(O(n\log n)\),散块重构:散块不超过\(2 \sqrt n\),共\(O(n\sqrt n\log n)\),访问前驱:散块直接暴力,整块每块内用lower_bound函数找,共\(O(n\sqrt n\log n)\),总复杂度\(O(n\sqrt n\log n)\)。
另一种做法是用set维护,预处理插入进set复杂度是\(O(n\log n)\),散块直接删除再插入,复杂度也是\(O(n\sqrt n\log n)\),访问前驱也是散块暴力,整块lower_bound,总复杂度两种方法相同,都是\(O(n\sqrt n\log n)\)。
我的代码使用了set,毕竟自动排序常数可能小点?(雾)
AC代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10,inf=0x3f3f3f3f;
int a[N],L[N],R[N],add[N],pos[N];
set<int>s[N];
int n;
void change(int l,int r,int k){
int p=pos[l],q=pos[r];
if(p==q){
for(int i=l;i<=r;i++){
s[pos[i]].erase(a[i]);
a[i]+=k;
s[pos[i]].insert(a[i]);
}
}
else{
for(int i=l;i<=R[p];i++){
s[pos[i]].erase(a[i]);
a[i]+=k;
s[pos[i]].insert(a[i]);
}
for(int i=p+1;i<=q-1;i++) add[i]+=k;
for(int i=L[q];i<=r;i++){
s[pos[i]].erase(a[i]);
a[i]+=k;
s[pos[i]].insert(a[i]);
}
}
}
int query(int l,int r,int k){
int p=pos[l],q=pos[r],ans=-1;
if(p==q){
for(int i=l;i<=r;i++){
if(a[i]+add[pos[i]]<k) ans=max(ans,a[i]+add[pos[i]]);
}
}
else{
for(int i=l;i<=R[p];i++){
if(a[i]+add[pos[i]]<k) ans=max(ans,a[i]+add[pos[i]]);
}
for(int i=p+1;i<=q-1;i++){
int d=k-add[i];
auto it=s[i].lower_bound(d);
if(it==s[i].begin()) continue;
it--;
ans=max(ans,*it+add[i]);
}
for(int i=L[q];i<=r;i++){
if(a[i]+add[pos[i]]<k) ans=max(ans,a[i]+add[pos[i]]);
}
}
return ans;
}
int main(){
cin>>n;
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
int t=sqrt(n);
for(int i=1;i<=t;i++) L[i]=(i-1)*t+1,R[i]=i*t;
if(R[t]<n) t++,L[t]=R[t-1]+1,R[t]=n;
for(int i=1;i<=t;i++){
s[i].insert(-1);
for(int j=L[i];j<=R[i];j++) pos[j]=i,s[i].insert(a[j]);
}
for(int i=1;i<=n;i++){
int opt,l,r,k;
scanf("%d%d%d%d",&opt,&l,&r,&k);
if(opt) printf("%d\n",query(l,r,k));
else change(l,r,k);
}
}
数列分块入门 4
题意:区间加法,区间求和。
分析:多维护一个数组sum,表示这个块的和,修改时散块也更新sum,整块也更新sum。
AC代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e4+10;
int a[N],L[N],R[N],add[N],pos[N],sum[N];
int n;
void change(int l,int r,int k){
int p=pos[l],q=pos[r];
if(p==q){
for(int i=l;i<=r;i++) a[i]+=k,sum[pos[i]]+=k;
}
else{
for(int i=l;i<=R[p];i++) a[i]+=k,sum[pos[i]]+=k;
for(int i=p+1;i<=q-1;i++) add[i]+=k,sum[i]+=(R[i]-L[i]+1)*k;
for(int i=L[q];i<=r;i++) a[i]+=k,sum[pos[i]]+=k;
}
}
int query(int l,int r){
int p=pos[l],q=pos[r],ans=0;
if(p==q){
for(int i=l;i<=r;i++) ans+=a[i]+add[pos[i]];
}
else{
for(int i=l;i<=R[p];i++) ans+=a[i]+add[pos[i]];
for(int i=p+1;i<=q-1;i++) ans+=sum[i];
for(int i=L[q];i<=r;i++) ans+=a[i]+add[pos[i]];
}
return ans;
}
signed main(){
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
int t=sqrt(n);
for(int i=1;i<=t;i++) L[i]=(i-1)*t+1,R[i]=i*t;
if(R[t]<n) t++,L[t]=R[t-1]+1,R[t]=n;
for(int i=1;i<=t;i++){
sum[i]=add[i]=0;
for(int j=L[i];j<=R[i];j++) pos[j]=i,sum[i]+=a[j];
}
for(int i=1;i<=n;i++){
int opt,l,r,k;
cin>>opt>>l>>r>>k;
if(opt) cout<<query(l,r)%(k+1)<<endl;
else change(l,r,k);
}
}


