算法笔记(1)线段树
原发表于个人博客。
前言
线段树,是数据结构皇冠上的明珠(我编的)。
它用途广泛,被一代代的oier应用,改进,优化。
本文介绍了线段树的基础知识和各种拓展(包括权值线段树,可持久化线段树),各种优化方式(包括zkw线段树,动态开点,离散化),希望能帮到更多的oier。
在学习线段树前,默认你应该学会一下内容:
- 树和二叉树的基本知识(这你总得会吧)
- 二叉堆(主要是堆式储存)
- 离散化(其实并不需要)
- 会写代码
如果你不会,左转oiwiki,如果你会,那么继续读吧!
线段树的引入
举个例子,我们现在有一个序列,想维护一段子区间的和,该怎么办呢?
你或许会说,可以暴力!把这个区间的数加起来就行了。
那么如果这个子区间里有1e5个数呢?
前缀和?
如果强制在线呢?
如果在维护区间和的同时维护最大值、并且支持区间修改呢?
我们有很多种办法维护区间问题,比如树状数组,线段树,分块。其中,线段树是较通用且直观的一种数据结构。
基础线段树
线段树入门
首先,我们有一个序列。
我们利用二分的思想,用每一个节点表示一个区间,两个子节点表示左右两个子区间。
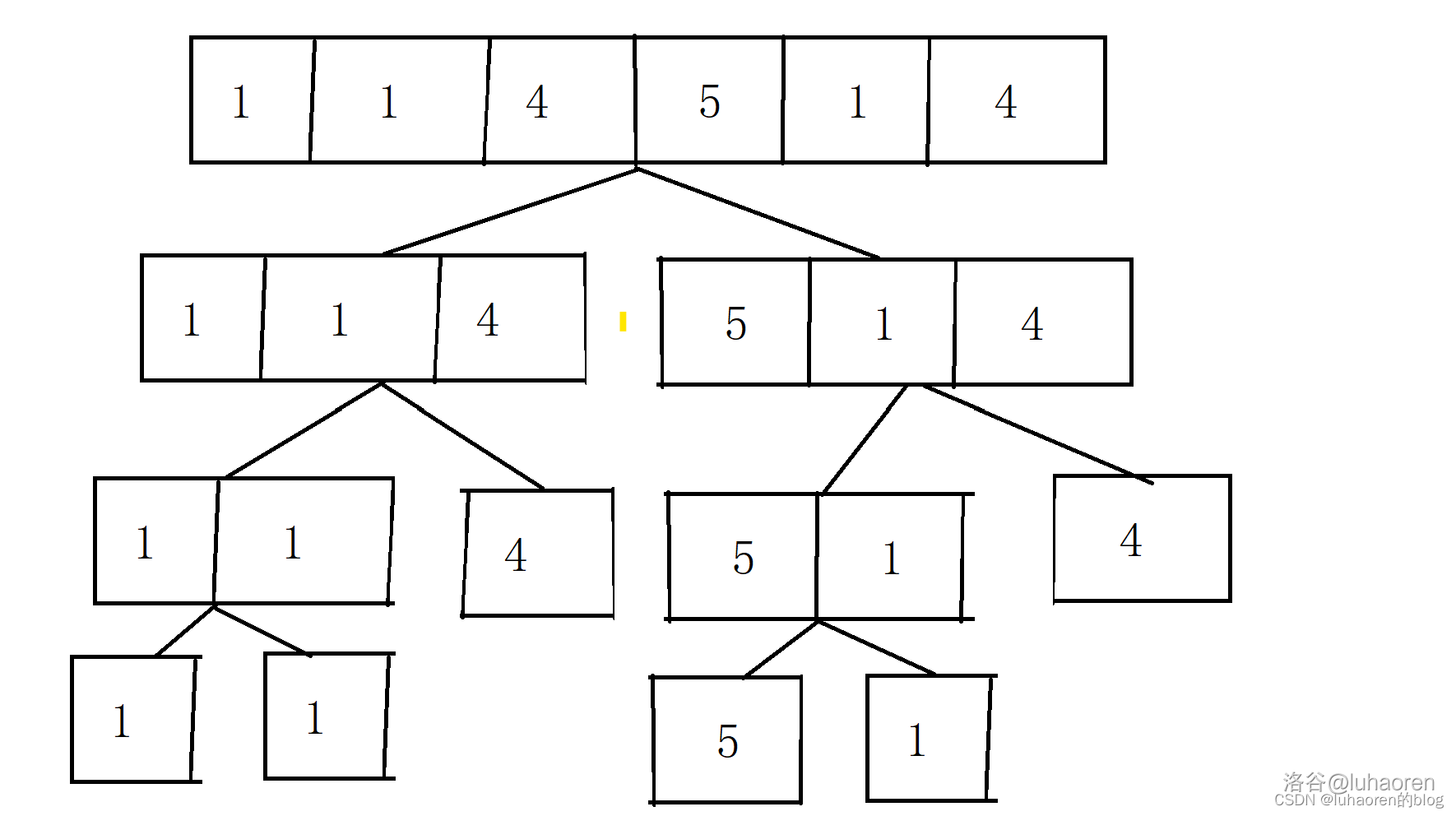
然后我们就可以在每个节点处维护一些信息。
注意:实际上,只有最下面一层的叶子节点才保存了实际的数字,其它的每个节点只保存着这个区间的信息(如区间和,区间最值等)
那么如何把子节点的信息传到父节点上呢?
我们要了解一个叫做\(pushup\)的操作。
void pushup(int x){
tr[x].sum=tr[x*2].sum+tr[x*2+1].sum;
}
这个操作的意思就是:节点表示的区间和等于两个子节点所表示的区间之和。即下图:

有了这个操作,我们就可以递归的求出每一个节点所表示的信息。
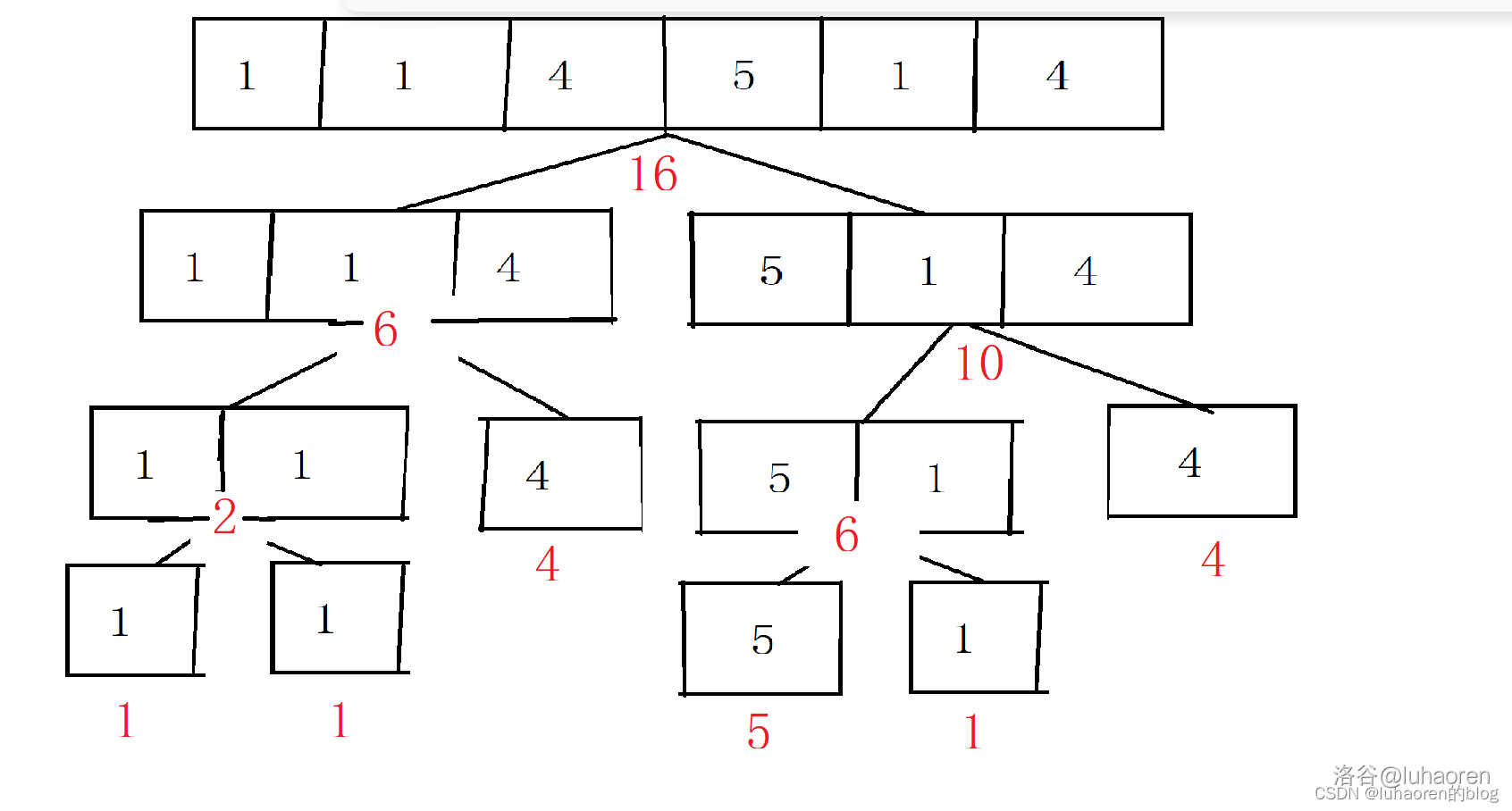
这个建立线段树的过程可以看作是预处理信息,把数组的信息转移到线段树的叶子节点上,时间复杂度大概是\(O(n)\)
事实上,还有另一种写法的线段树,不需要建树,但是需要\(O( n\log n)\)的时间复杂度插入数据,我们会在权值线段树部分介绍这种写法。
建树代码
void build(int x,int l,int r){
tr[x].l=l,tr[x].r=r;//节点表示区间的左右界
if(l==r){
//若l=r,说明这个节点是叶子节点,直接赋值
tr[x].sum=a[l];//a是原数列
return;
}
int mid=(l+r)/2;//mid表示左右子区间的间隔
build(x*2,l,mid),build(x*2+1,mid+1,r);//递归建树
//线段树是完全二叉树,左右子节点可以用x*2,x*2+1表示
tr[x].sum=tr[x*2].sum+tr[x*2+1].sum;//pushup操作
}
区间查询
线段树可以在\(O(\log n)\)的时间复杂度下完成区间查询操作。
以刚刚的数列\(\left \{ 1,1,4,5,1,4 \right \}\)为例。
此时如果询问\([3,5]\)之间的区间和,我们该怎么办呢?

首先,如果直接查询\([4,6]\)的区间和,我们肯定是会的,直接输出10就行。
查询\([4,5]\)怎么办呢?
可以把\([4,6]\)拆成\([4,5]\)和\([6,6]\),然后输出\([4,5]\)的和。
那么\([3,5]\)就可以表示为\([3,3]\)和\([4,5]\)。
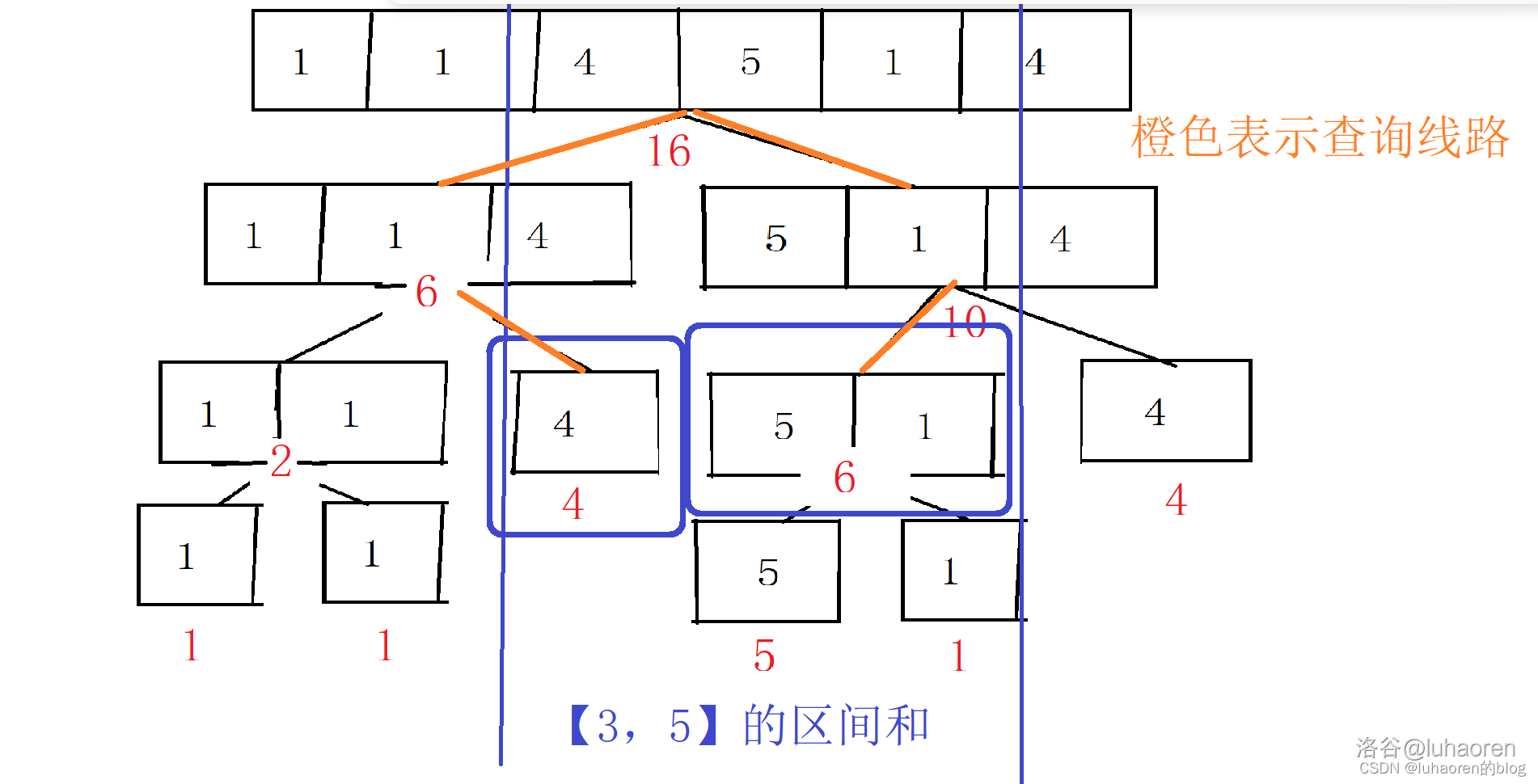
所以无论我们查询多大的区间,都可以拆成一些(不超过\(\log n\))预处理过的子区间,把这些子区间的区间和加起来,就是答案。
区间查询代码
int query(int x,int l,int r){
//区间查询
if(tr[x].l>=l&&tr[x].r<=r) return tr[x].sum;//如果该节点的区间被要查找的区间包括了,那么就不用继续找了,直接返回改节点的值就行了
int mid=(tr[x].l+tr[x].r)/2;
int sum=0;
if(l<=mid) sum+=query(x*2,l,r);//如果当前节点在要查找区间左边界的右面,那么递归查找左子树
if(r>mid) sum+=query(x*2+1,l,r);//如果当前节点在要查找区间右边界的左面,那么递归查找右子树
return sum;//由此得出了该区间的值,返回即可
}
单点修改
单点修改比较简单,不断递归,定位到要找的节点,修改即可。

单点修改代码
void change(int now,int x,int k){
//单点修改
if(tr[now].l==tr[now].r){
tr[now].sum=k;//如果找到了该节点,那么修改它
return;
}
int mid=(tr[now].l+tr[now].r)/2;
if(x<=mid) change(now*2,x,k);//如果要寻找的节点在当前节点的左侧,就递归左子树
else change(now*2+1,x,k);//否则递归右子树
tr[now].sum=tr[now*2].sum+tr[now*2+1].sum;//pushup操作,维护每个节点的sum值
}
线段树的存储
观察线段树,我们发现它是一个完全二叉树,可以用堆式储存法。
即把每个节点都存在一个数组里,因为是完全二叉树,所以两个子节点可以用\(2p\),\(2p+1\)表示。
因为线段树大部分节点都不是用来存数字的,所以线段树所用的空间要比原数列的空间多很多,如图,只有红色的节点才是真正存数字的。

线段树大概要开四倍的空间,具体可以看OIwiki上的分析。
例题1:单点修改,区间查询
已知一个数列,进行下面两种操作:
- 将某一个数加上\(x\)
- 求出某区间每一个数的和
题目分析
相当于模板题,可以尝试着敲一遍,这里提供代码。
AC代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+10;
struct node{
int sum,l,r;//线段树节点的结构体
}tr[N*4];//线段树需要开四倍空间
int a[N];
inline void pushup(int x){
tr[x].sum=tr[x*2].sum+tr[x*2+1].sum;
}
void build(int x,int l,int r){
tr[x].l=l,tr[x].r=r;//节点表示区间的左右界
if(l==r){
//若l=r,说明这个节点是叶子节点,直接赋值
tr[x].sum=a[l];//a是原数列
return;
}
int mid=(l+r)/2;//mid表示左右子区间的间隔
build(x*2,l,mid),build(x*2+1,mid+1,r);//递归建树
//线段树是完全二叉树,左右子节点可以用x*2,x*2+1表示
pushup(x);//pushup操作
}
int query(int x,int l,int r){
//区间查询
if(tr[x].l>=l&&tr[x].r<=r) return tr[x].sum;//如果该节点的区间被要查找的区间包括了,那么就不用继续找了,直接返回改节点的值就行了
int mid=(tr[x].l+tr[x].r)/2;
int sum=0;
if(l<=mid) sum+=query(x*2,l,r);//如果当前节点在要查找区间左边界的右面,那么递归查找左子树
if(r>mid) sum+=query(x*2+1,l,r);//如果当前节点在要查找区间右边界的左面,那么递归查找右子树
return sum;//由此得出了该区间的值,返回即可
}
void change(int now,int x,int k){
//单点修改
if(tr[now].l==tr[now].r){
tr[now].sum+=k;//如果找到了该节点,那么修改它
return;
}
int mid=(tr[now].l+tr[now].r)/2;
if(x<=mid) change(now*2,x,k);//如果要寻找的节点在当前节点的左侧,就递归左子树
else change(now*2+1,x,k);//否则递归右子树
pushup(now);//pushup操作,维护每个节点的sum值
}
int n,q;
int main(){
cin>>n>>q;
for(int i=1;i<=n;i++) cin>>a[i];
build(1,1,n);//建树
while(q--){
int t,b,c;
cin>>t>>b>>c;
if(t==1) change(1,b,c);
else cout<<query(1,b,c)<<endl;
}
}
习题
学会了线段树最基础的部分,就可以做一些习题了,将在博客的最后提供题解和代码。
- JSOI2008 最大数
线段树维护最大值的模板 - loj10123. Balanced Lineup
RMQ问题,可以试试用线段树做
懒标记
下面请思考,怎么才能做到线段树的区间修改呢?
如果直接把区间遍历一遍,依次修改,复杂度会达到无法接受的\(O(n\log n)\)。
那么怎么能让区间修改的复杂度变小呢?
我们需要引入一个叫做“懒标记”的东西。
懒标记也叫延迟标记,顾名思义,我们再修改这个区间的时候给这个区间打上一个标记,这样就可以做到区间修改的\(O(\log n)\)的时间复杂度。
如图,如果要给\([4,6]\)每个数都加上\(2\),那么直接再代表着\([4,6]\)区间的结点打上\(+2\)的标记就行了。

pushdown操作
再想一个问题,在给\([4,6]\)区间打上懒标记后,我们如何查询\([4,5]\)的值?
如果我们直接查询到\([4,5]\)区间上,会发现根本就没有被加上过2。
为什么呢?
因为现在懒标记打在了\([4,6]\)区间上。而他的子节点压根没被修改过!
所以我们需要把懒标记向下传递。
这就有了一个操作,叫做pushdown,它可以把懒标记下传。
设想一下,如果我们要把懒标记下传,应该注意什么呢?
首先,要给子节点打上懒标记。
然后,我们要修改子节点上的值。
最后,不要忘记把这个节点的懒标记清空。
pushdown代码
inline void pushudown(int x){
if(tr[x].add){
//如果这个节点上有懒标记
tr[2*x].add+=tr[x].add,tr[2*x+1].add+=tr[x].add;
//把这个节点的懒标记给他的两个子节点
tr[2*x].sum+=tr[x].add*(tr[2*x].r-tr[2*x].l+1);
tr[2*x+1].sum+=tr[x].add*(tr[2*x+1].r-tr[2*x+1].l+1);
//分别给它的两个子节点修改
tr[x].add=0;
//别忘了清空这个节点的懒标记
}
}
区间修改
学会了懒标记,应该可以很轻松地写出区间修改的代码了。
区间修改的操作很像区间查询,也是查找能够覆盖住的子区间,然后给它打上懒标记。
区间查询代码
void update(int now,int l,int r,int k){
if(l<=tr[now].l&&r>=tr[now].r){
//如果查到子区间了
tr[now].sum+=k*(tr[now].r-tr[now].l+1);//先修改这个区间
tr[now].add+=k;//然后给它打上懒标记
//注:这里一定要分清顺序,先修改,再标记!
}
else{
//如果需要继续向下查询
pushudown(now);//一定要先把懒标记向下传
int mid=(tr[now].l+tr[now].r)/2;
//这里很像区间查询
if(l<=mid) update(now*2,l,r,k);
if(r>mid) update(now*2+1,l,r,k);
//最后别忘了pushup一下
pushup(now);
}
}
例题2:区间修改,区间查询
已知一个数列,你需要进行下面两种操作:
- 将某区间每一个数加上\(k\)。
- 求出某区间每一个数的和。
题目分析
应用到区间修改,需要注意的一点是,在区间查询时,也需要下传懒标记,这样才能查询到真实的值。
AC代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
struct node{
int sum;
int l,r;
int add;//懒标记
}tr[N*4];//线段树要开四倍空间哦
int a[N];//原数列
inline void pushup(int x){
tr[x].sum=tr[2*x].sum+tr[2*x+1].sum;//pushup操作
}
inline void pushudown(int x){
if(tr[x].add){
//如果这个节点上有懒标记
tr[2*x].add+=tr[x].add,tr[2*x+1].add+=tr[x].add;
//把这个节点的懒标记给他的两个子节点
tr[2*x].sum+=tr[x].add*(tr[2*x].r-tr[2*x].l+1);
tr[2*x+1].sum+=tr[x].add*(tr[2*x+1].r-tr[2*x+1].l+1);
//分别给它的两个子节点修改
tr[x].add=0;
//别忘了清空这个节点的懒标记
}
}
void build(int x,int l,int r){
//建树操作
tr[x].l=l,tr[x].r=r,tr[x].add=0;
if(l==r){
tr[x].sum=a[l];
return;
}
int mid=(l+r)/2;
build(2*x,l,mid),build(2*x+1,mid+1,r);
pushup(x);
}
int query(int x,int l,int r){
if(l<=tr[x].l&&r>=tr[x].r) return tr[x].sum;
pushudown(x);//注意,区间查询时也要下懒传标记
int mid=(tr[x].l+tr[x].r)/2,sum=0;
if(l<=mid) sum+=query(x*2,l,r);
if(r>mid) sum+=query(x*2+1,l,r);
return sum;
}
void update(int now,int l,int r,int k){
if(l<=tr[now].l&&r>=tr[now].r){
//如果查到子区间了
tr[now].sum+=k*(tr[now].r-tr[now].l+1);//先修改这个区间
tr[now].add+=k;//然后给它打上懒标记
//注:这里一定要分清顺序,先修改,再标记!
}
else{
//如果需要继续向下查询
pushudown(now);//先把懒标记向下传
int mid=(tr[now].l+tr[now].r)/2;
//这里很像区间查询
if(l<=mid) update(now*2,l,r,k);
if(r>mid) update(now*2+1,l,r,k);
pushup(now);//最后别忘了pushup一下
}
}
int n,q;
int main(){
cin>>n>>q;
for(int i=1;i<=n;i++) cin>>a[i];
build(1,1,n);
while(q--){
int l,r,k,c;
cin>>c>>l>>r;
if(c==1){
cin>>k;
update(1,l,r,k);
}
else cout<<query(1,l,r)<<endl;
}
return 0;
}
//别忘了开long long哦
例题3:较复杂的区间操作
已知一个数列,你需要进行下面三种操作:
-
将某区间每一个数乘上\(x\)。
-
将某区间每一个数加上\(x\)。
-
求出某区间每一个数的和。
题目分析
有些题要维护多个区间操作,这在pushdown操作上就比较麻烦,比如这道题,要求维护区间加法和区间乘法,所以我们得维护两个懒标记。
那么我们该怎样安排懒标记的pushdown顺序呢?
我们考虑先乘后加的维护顺序,假设两个懒标记分别是\(mul\)和\(add\),那么这个数值就应该是\(mul \times sum+add\)。
此时如果加上一个\(add\),就会变成 \(mul \times sum+add+add\)
如果乘上一个\(mul\)那就是\(mul \times sum \times mul+add \times mul\)
这种方式便于计算,如果使用先加后乘的方式,就会比较麻烦甚至会出错。
AC代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
struct node{
int l,r;
int sum,add,mul;
}tr[N*4];//线段树开四倍空间
int a[N];
int n,p,m;
inline void pushup(int x){
tr[x].sum=(tr[2*x].sum+tr[2*x+1].sum)%p;
}
inline void eval(int x,int add,int mul){
//我们把计算懒标记单独放在这个函数里,否则好多东西挤一块很难看
tr[x].sum=(tr[x].sum*mul+add*(tr[x].r-tr[x].l+1))%p;
tr[x].mul=(mul*tr[x].mul)%p; //先计算乘法懒标记
tr[x].add=(tr[x].add*mul+add)%p;//再算加法懒标记
}
inline void pushdown(int x){
//依次计算两个子节点的值和懒标记
eval(x*2,tr[x].add,tr[x].mul);
eval(x*2+1,tr[x].add,tr[x].mul);
tr[x].add=0,tr[x].mul=1;
//清空懒标记,注意:乘法懒标记要初始化成1
}
void build(int x,int l,int r){
tr[x].l=l,tr[x].r=r;
tr[x].add=0,tr[x].mul=1;//乘法懒标记要初始化成1
if(l==r){
tr[x].sum=a[l];
return;
}
int mid=(l+r)/2;
build(x*2,l,mid),build(x*2+1,mid+1,r);//递归建树
pushup(x);
}
void change(int x,int l,int r,int add,int mul){
if(l<=tr[x].l&&r>=tr[x].r) eval(x,add,mul);//计算
else{
pushdown(x);
int mid=(tr[x].l+tr[x].r)/2;
if(l<=mid) change(x*2,l,r,add,mul);
if(r>mid) change(x*2+1,l,r,add,mul);
pushup(x);
}
}
int query(int x,int l,int r){
if(l<=tr[x].l&&r>=tr[x].r) return tr[x].sum;
int sum=0;
pushdown(x); //区间查询时也要pushdown
int mid=(tr[x].l+tr[x].r)/2;
if(l<=mid) sum+=query(x*2,l,r)%p;
if(r>mid) sum+=query(x*2+1,l,r)%p;
return sum;
}
int main(){
int t,g,c,ch;
cin>>n>>m>>p;
for(int i=1;i<=n;i++) cin>>a[i];
build(1,1,n);
while(m--){
cin>>ch>>t>>g;
if(ch==1){
cin>>c;
change(1,t,g,0,c);
}
else if(ch==2){
cin>>c;
change(1,t,g,c,1);
}
else cout<<query(1,t,g)%p<<endl;
}
return 0;
}
//记得开longlong
标记永久化
其实,维护区间修改的方式有两种,一种是懒标记和标记下传,另一种叫做”标记永久化“。
标记永久化,就是不下传标记,在每次查询时把经过的标记累加起来,查询时加起来。

如图,打上标记的节点用绿色表示,查询路线(橙色)经过的就累加。
标记永久化代码
const int N=1e4+10;
struct node{
int sum,add;
int l,r;
}tr[N*4];
int a[N];
void build(int x,int l,int r){
tr[x].l=l,tr[x].r=r;
if(l==r){
tr[x].sum=a[l],tr[x].add=0;
return;
}
int mid=(l+r)/2;
build(x*2,l,mid),build(x*2+1,mid+1,r);
tr[x].sum=tr[x*2].sum+tr[x*2+1].sum;//标记永久化中只有建树时需要用到pushup操作
}
void update(int x,int l,int r,int k){
tr[x].sum+=(min(tr[x].r,r)-max(tr[x].l,l)+1)*k;//要取一个交集来加
if(tr[x].l>=l&&tr[x].r<=r){
tr[x].add+=k;//给节点打上标记后不用下传。
return;
}
int mid=(tr[x].l+tr[x].r)/2;
if(l<=mid) update(x*2,l,r,k);
if(r>mid) update(x*2+1,l,r,k);
}
int query(int x,int l,int r,int add){
if(tr[x].l>=l&&tr[x].r<=r){
int s=(tr[x].r-tr[x].l+1)*add;//查询到节点后给这个区间乘上add
return tr[x].sum+s;
}
add+=tr[x].add;//add代表查询经过的懒标记之和
int mid=(tr[x].l+tr[x].r)/2,sum=0;
if(l<=mid) sum+=query(x*2,l,r,add);
if(r>mid) sum+=query(x*2+1,l,r,add);
return sum;
}
标记永久化应用很多,比如可持久化线段树中的区间修改,树套树中第二维的修改。(后面都将讲到)
习题
这里给出一些习题,按照难度排序。
- AHOI2009 维护序列
与例题3差不多 - 洛谷P1253 扶苏的问题
稍微复杂的懒标记维护 - 洛谷P5142 区间方差
需要一定的数学推导能力 - P4145 花神游历各国
想一想如何优化? - P1471 方差
3题的加强版,较难 - P6327 区间加区间sin和
需要一些高中的数学知识
权值线段树
权值线段树是线段树的一种衍生算法,其基本存储结构和线段树基本相同。
权值线段树与线段树的不同点在于,线段树维护区间信息,权值线段树维护值域信息。
如图,权值线段树就长这个样子。
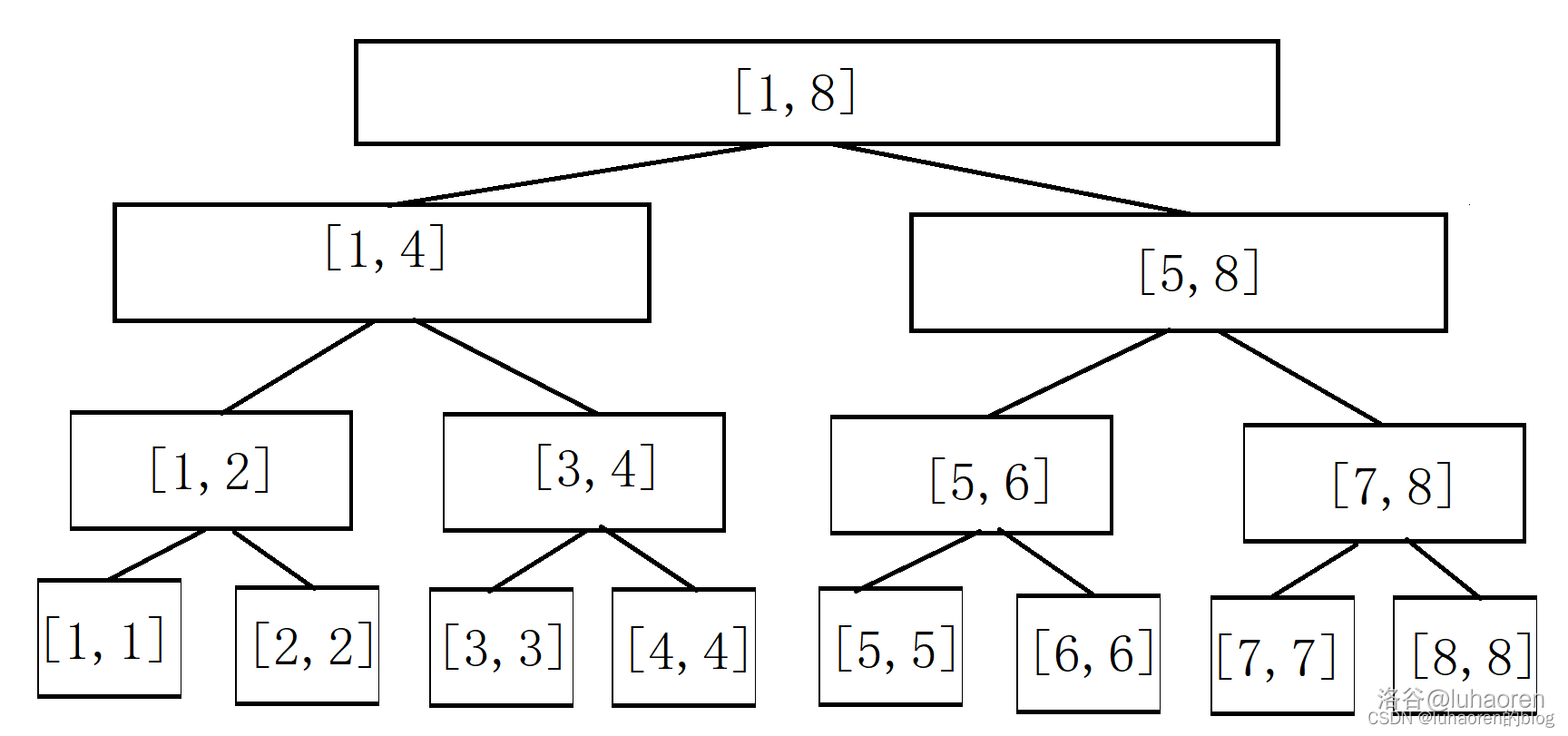
看起来和线段树没什么区别吧,现在我们插入一个数\(4\)。
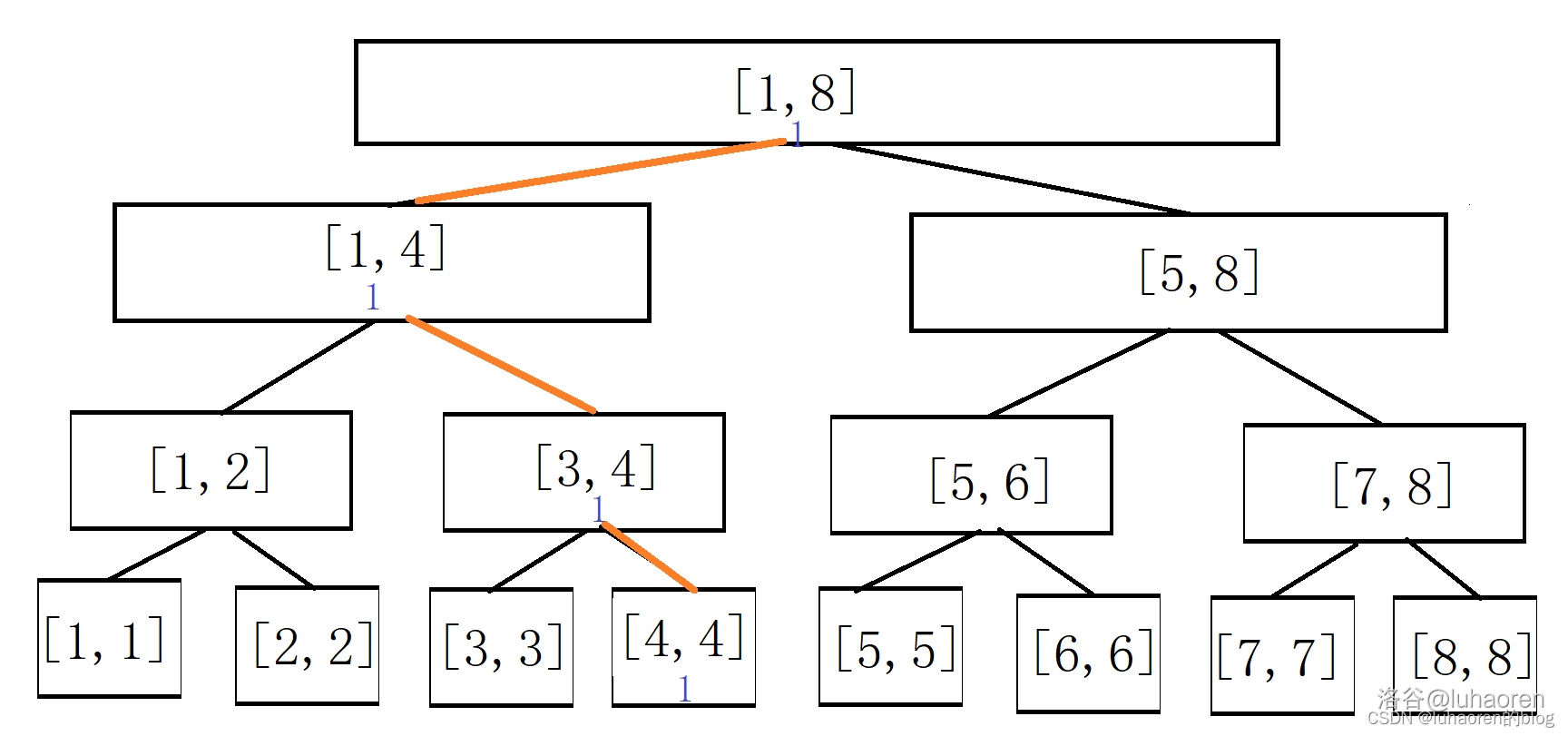
每一个包含\(4\)的区间都被加上了1。
那么每个区间维护的到底是什么呢?
是这个区间内的数的数量。
当我们依次插入\(\{4,1,7,2,8 \}\)后,这个权值线段树就变成了这样。
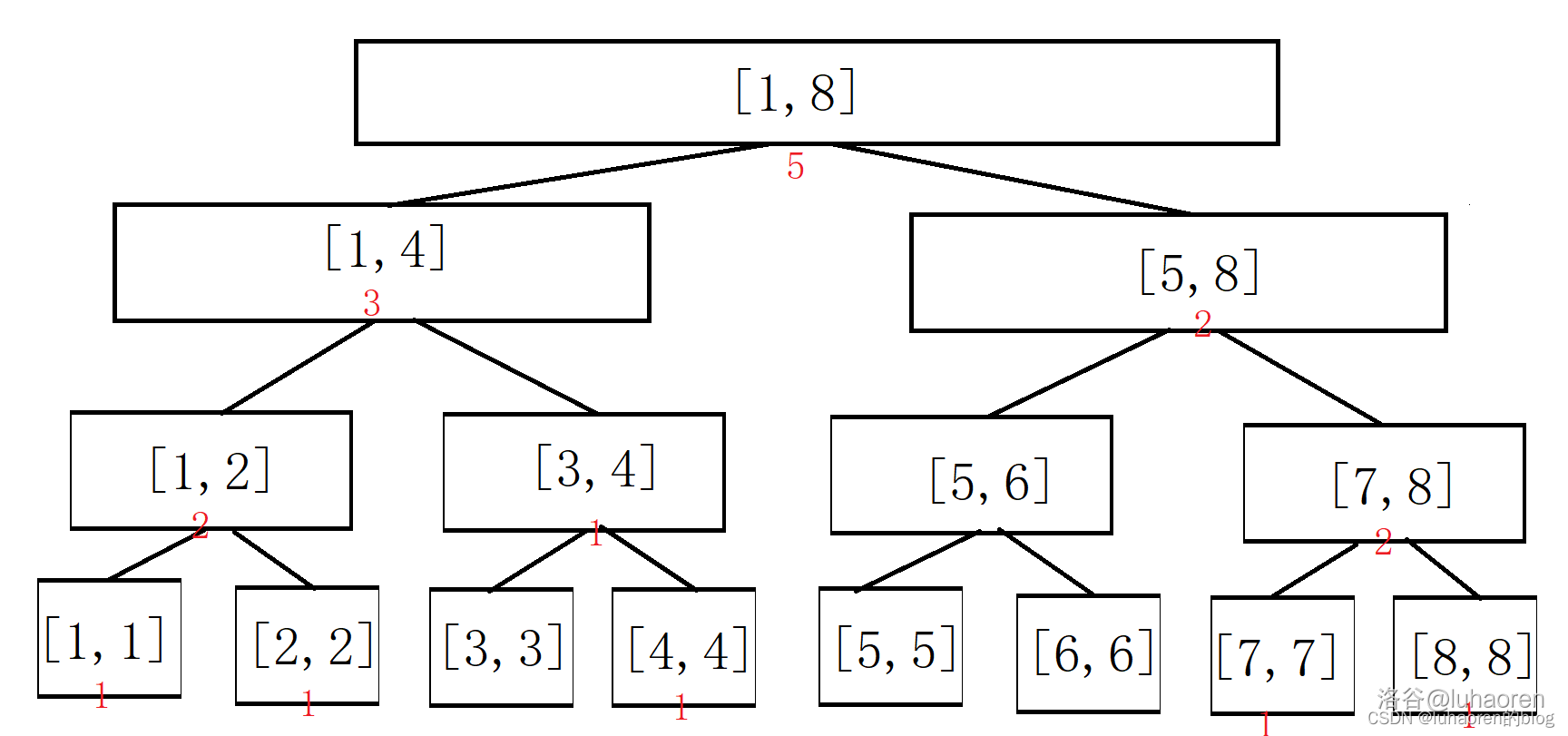
这就是权值线段树的原理。
权值线段树可以干很多事情,比如查询第\(k\)小,查找前驱后继等。
插入与删除
想一想,我们该如何实现插入一个数的操作呢?
把从这个数的节点到根节点的路径上每一个节点都加上1即可。
删除呢?
减去1就行了。
代码模板
int tr[N*4];
//这就是上文提到过的线段树的另一种写法,因为权值线段树不需要维护区间信息,所以不需要建树的预处理,这种写法就变得很方便。
inline void pushup(int x){
tr[x]=tr[x*2]+tr[x*2+1];
}
void insert(int x,int l,int r,int k){
//插入一个数k
if(l==r){
tr[x]++;
return;
}
int mid=(l+r)/2;
if(k<=mid) insert(x*2,l,mid,k);
else insert(x*2+1,mid+1,r,k);
pushup(x);
}
void del(int x,int l,int r,int k){
//删除一个数k
if(l==r){
tr[x]--;
return;
}
int mid=(l+r)/2;
if(k<=mid) del(x*2,l,mid,k);
else del(x*2+1,mid+1,r,k);
pushup(x);
}
int query(int x,int l,int r,int ql,int qr){
//查询ql,qr之间一共有多少个数
if(l>=ql&&r<=qr) return tr[x];
int mid=(l+r)/2,sum=0;
if(ql<=mid) sum=query(x*2,l,mid,ql,qr);
if(qr>mid) sum+=query(x*2+1,mid+1,r,ql,qr);
return sum;
}
例题4:权值线段树
NK 中学组织同学们去五云山寨参加社会实践活动,按惯例要乘坐火车去。由于 NK 中学的学生很多,在火车开之前必须清点好人数。
初始时,火车上没有学生。当同学们开始上火车时,年级主任从第一节车厢出发走到最后一节车厢,每节车厢随时都有可能有同学上下。年级主任走到第\(m\)节车厢时,他想知道前\(m\)节车厢上一共有多少学生。每次提问,m 总会比前一次大。
题目分析
很明显可以用权值线段树做,维护每个区间的数的数量,具体见代码。
AC代码
#include <bits/stdc++.h>
using namespace std;
const int N=5e5+10;
int tr[N*4];//权值线段树维护的是值域,所以要开n的范围的四倍
inline void pushup(int x){
tr[x]=tr[x*2]+tr[x*2+1];
}
void insert(int x,int l,int r,int k,int p){
if(l==r){
tr[x]+=p;
return;
}
int mid=(l+r)/2;
if(k<=mid) insert(x*2,l,mid,k,p);
else insert(x*2+1,mid+1,r,k,p);
pushup(x);
}
int query(int x,int l,int r,int ql,int qr){
if(l>=ql&&r<=qr) return tr[x];
int mid=(l+r)/2,sum=0;
if(ql<=mid) sum=query(x*2,l,mid,ql,qr);
if(qr>mid) sum+=query(x*2+1,mid+1,r,ql,qr);
return sum;
}
int n,k;
int main(){
cin>>n>>k;
while(k--){
char opt;
int m,p;
cin>>opt;
if(opt=='A'){
cin>>m;
cout<<query(1,1,n,1,m)<<endl;
}
else if(opt=='B'){
//上车
cin>>m>>p;
insert(1,1,n,m,p);
}
else{
//下车
cin>>m>>p;
insert(1,1,n,m,-p);
}
}
}
查询第k大数
请注意,这个查询第k大是针对整个权值线段树的,要查区间第k大请去学主席树或树套树。
权值线段树是维护值域的,一个节点的左右端点都应该是一个具体的数字,而且值域肯定是递增的,所以我们可以二分。
如果 \(k\)小于区间中点,那么也就说明结果为左区间第\(k\)大数。否则,也就说明结果为右区间第\(k−l_{size}\)大数。
代码
int kth(int x,int l,int r,int k){
if(l==r) return l;//查到了,返回即可
int mid=(l+r)/2;
if(k<=tr[x*2]) return kth(x*2,l,mid,k);
return kth(x*2+1,mid+1,r,k-tr[x*2]);
}
查询一个数的排名
和查询第k大差不多。
每次把\(x\)与当前区间中点\(mid\)比较,如果小于等于\(mid\),说明在左区间,向左儿子寻找。
如果大于\(mid\),说明在右区间,这时,它的排名要加上左子树的大小(它比整个左子树的数都大)
如果找到叶子节点了,那么返回\(1\)(在\([l,r]\)的区间只有自己,排名第一)
代码
int rnk(int x,int l,int r,int k){
if(l==r) return 1;
int mid=(l+r)/2;
if(k<=mid) return rnk(x*2,l,mid,k);
return rnk(x*2+1,mid+1,r,k)+tr[x*2];
}
例题5:用权值线段树实现平衡树
实现一个数据结构,来维护一些数,其中需要提供以下操作:
- 插入\(x\)数
- 删除\(x\)数(若有多个相同的数,应只删除一个)
- 查询\(x\)数的排名(排名定义为比当前数小的数的个数\(+1\))
- 查询排名为\(x\)的数
- 求\(x\)的前驱(前驱定义为小于\(x\),且最大的数)
- 求\(x\)的后继(后继定义为大于\(x\),且最小的数)
题目分析
正宗解法自然是平衡树,但是仔细观察这些操作,似乎都可以用权值线段树解决?
前四个操作我们已经讲解过了,只剩下最后两个:求前驱和后继。
前驱实际上就是比\(x\)的排名小一位的数,也就是kth(rnk(x)-1)。
后继就是\(x+1\)的排名位置的数,也就是kth(rnk(x+1))。
那么我们就可以写出代码了?
没AC代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e7+10;
int tr[8*N];//因为要维护正负区间,所以开二倍,再加线段树的四倍空间,就是八倍
inline void pushup(int x){
tr[x]=tr[x*2]+tr[x*2+1];
}
void insert(int x,int l,int r,int k,int p){
//若p为1则插入,若p为-1则删除
if(l==r){
tr[x]+=p;
return;
}
int mid=(l+r)/2;
if(k<=mid) insert(x*2,l,mid,k,p);
else insert(x*2+1,mid+1,r,k,p);
pushup(x);
}
int kth(int x,int l,int r,int k){
//查询排名为k的数
if(l==r) return l;
int mid=(l+r)/2;
if(k<=tr[x*2]) return kth(x*2,l,mid,k);
return kth(x*2+1,mid+1,r,k-tr[x*2]);
}
int rnk(int x,int l,int r,int k){
//查找数k的排名
if(l==r) return 1;
int mid=(l+r)/2;
if(k<=mid) return rnk(x*2,l,mid,k);
return rnk(x*2+1,mid+1,r,k)+tr[x*2];
}
int n;
int main(){
cin>>n;
while(n--){
int opt,x;
cin>>opt>>x;
switch(opt){
case 1:
insert(1,-N,N,x,1);//插入
break;
case 2:
insert(1,-N,N,x,-1);//删除
break;
case 3:
cout<<rnk(1,-N,N,x)<<endl;
break;
case 4:
cout<<kth(1,-N,N,x)<<endl;
break;
case 5:
cout<<kth(1,-N,N,rnk(1,0,N,x)-1)<<endl;
break;
case 6:
cout<<kth(1,-N,N,rnk(1,0,N,x)+1)<<endl;
break;
}
}
}
细心的你会发现,这个线段树怎么开了\(8\times10^7\)呢?肯定会爆空间啊。
但是题目要求的\(|x|\le10^7\)却令我们不得不开这么大。
怎么办呢?
一般来说,优化线段树空间的有两种方法。
一种是离散化后再进行操作(离线),一种是动态开点。
(这两种方法都会在下一节介绍到)
在这道题中,我们可以使用动态开点的方式,优化空间。
‘动态开点代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e7+10,M=4e5+10;
int tr[M];
int ls[M],rs[M],tot=0;
inline void pushup(int x){
tr[x]=tr[ls[x]]+tr[rs[x]];//动态开点后,就不能用x*2的方式存了,得开lsrs两个数组(或结构体)
}
void insert(int &x,int l,int r,int k,int p){//x是引用形式,方便传值
if(!x) x=++tot;//动态开点
//若p为1则插入,若p为-1则删除
if(l==r){
tr[x]+=p;
return;
}
int mid=(l+r)/2;
if(k<=mid) insert(ls[x],l,mid,k,p);
else insert(rs[x],mid+1,r,k,p);
pushup(x);
}
int kth(int x,int l,int r,int k){
if(l==r) return l;//查到了,返回即可
int mid=(l+r)/2;
if(k<=tr[ls[x]]) return kth(ls[x],l,mid,k);
return kth(rs[x],mid+1,r,k-tr[ls[x]]);
}
int rnk(int x,int l,int r,int k){
if(l==r) return 1;
int mid=(l+r)/2;
if(k<=mid) return rnk(ls[x],l,mid,k);
return rnk(rs[x],mid+1,r,k)+tr[ls[x]];
}
int n,root;
int main(){
cin>>n;
while(n--){
int opt,x;
cin>>opt>>x;
switch(opt){
case 1:
insert(root,-N,N,x,1);//因为动态开点的插入写成引用形式,所以需要带进去一个变量
break;
case 2:
insert(root,-N,N,x,-1);//删除
break;
case 3:
cout<<rnk(root,-N,N,x)<<endl;
break;
case 4:
cout<<kth(root,-N,N,x)<<endl;
break;
case 5:
cout<<kth(root,-N,N,rnk(root,-N,N,x)-1)<<endl;
break;
case 6:
cout<<kth(root,-N,N,rnk(root,-N,N,x+1))<<endl;
break;
}
}
}
如果想学习离散化的解法,可以看这位%%%的博客。
空间优化技巧
这里介绍两种优化方式:离散化和动态开点。
两种方法其实各有优劣,如果只是为了缩小值域,离散化似乎更好写一点,但是动态开点还可以被应用到可持久化、线段树合并和分裂上,所以都学一学吧。
离散化
数据范围太大了,需要缩小数据范围,这句话让你想到了什么?
当然是离散化了!
所以我们可以把所有操作都存起来,排序然后离散化,离线进行操作。
如果你不会离散化,请看这篇博客。
动态开点
动态开点,顾名思义,就是使用的时候再开点。
如果数据范围是\([-10^7,10^7]\),在权值线段树的使用过程中,很大一部分的节点会使用不到,这会造成一种浪费。
动态开点的意思就是:不一上来就把所有的节点全部建立起来,只在需要用到一个节点的时候再建立一个节点。
注意:使用动态开点线段树的话,节点的下标将是无序的,因此必须建立结构体或用两个数组来分别保存一个节点的左右子节点。
代码模板
int tr[M];
int ls[M],rs[M],tot=0;
inline void pushup(int x){
tr[x]=tr[ls[x]]+tr[rs[x]];//动态开点后,就不能用x*2的方式存了,得开lsrs两个数组(或结构体)
}
void insert(int &x,int l,int r,int k){//x是引用形式,方便传值
if(!x) x=++tot;//动态开点
if(l==r){
tr[x]++;
return;
}
int mid=(l+r)/2;
if(k<=mid) insert(ls[x],l,mid,k);
else insert(rs[x],mid+1,r,k);
pushup(x);
}
习题
提供几道权值线段树的习题。
- loj10114.数星星 Stars
权值线段树,需要用动态开点或离散化的优化 - P1168 中位数
离散化,然后开权值线段树维护 - P2073 送花
可以用权值线段树做 - SDOI2014 旅行
树链剖分(如果你会的话),用动态开点维护
zkw线段树
zkw线段树是一种用循环实现的线段树,比正常的递归式线段树快很多,而且好写。
zkw线段树的引入
我们观察一个线段树的结构,按照堆式储存,叶子节点的序号是连续的。
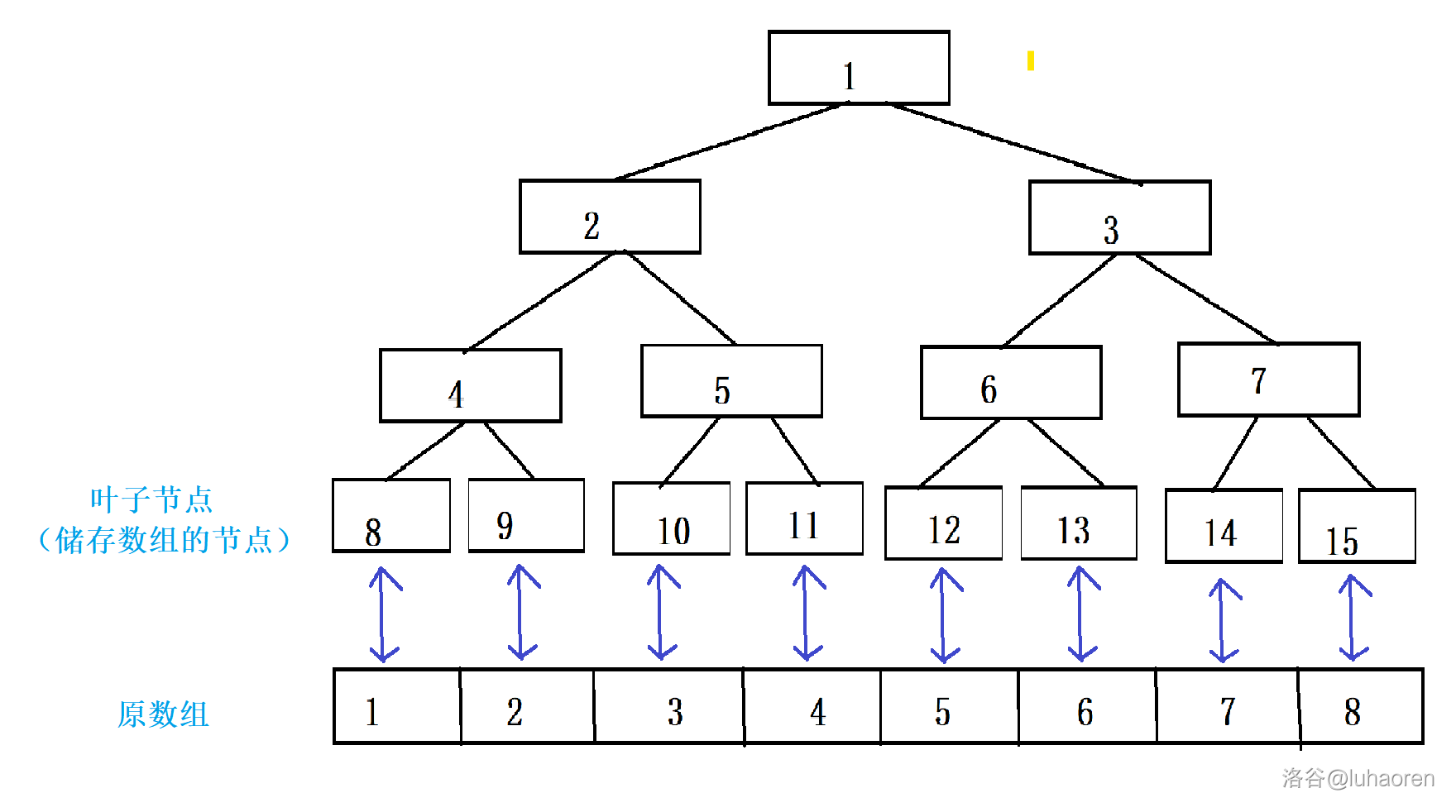
而原数组中的数字编号也恰恰是连续的,所以二者之间有一个对应关系。
仔细观察,发现两者序号之差竟然是一个定值。
所以,我们就可以快速地找到数字在线段树中的位置,即x+N(N为差值)。
而这个\(N\)就应该是线段树中抛去叶子节点之外的节点的数量。
为了方便,我们约定,无论树有没有那么大,我们都把\(N\)看作\(n\),无数据的叶节点空置即可。
这样我们就可以通过循环的方式,完成线段树的初始化。
建树代码
int tr[N*4];//zkw线段树不用维护子区间,直接开数组就行
int n,m;
void build(){
cin>>n>>m;
for(int i=n+1;i<=2*n;i++) cin>>tr[i];//直接读入到叶子节点里
for(int i=n-1;i>=1;i--) tr[i]=tr[i*2]+tr[i*2+1];//自底向上更新
}
建树才三行代码,还包括了读入,zkw线段树是不是很神奇?
单点修改&区间查询
单点修改
找到了数字在线段树中的位置,怎么更新它的父节点呢?
按照堆式储存的特点,节点的父节点就应该是\(x/2\)(x是这个节点)
那么从叶子节点开始,一步步地向上爬,更新,就完成了一次单点修改。
这也是zkw线段树的一个特色——自底向上。

单点修改代码
inline void change(int x,int k){//给x加上k
for(int i=x+=n;i;i/=2) tr[i]+=k;//自底向上更新
}
看完单点修改,相信大家已经会了单点查询,那就是:
单点查询代码
inline int query_one(int x){//查询x值
return tr[x+n];
}
区间查询
接下来思考,如何做到区间查询呢?
如图,以查询\([3,6]\)区间之和为例,我们先设两个指针\(p,q\),让\(p=l-1,q=r+1\)。

然后让\(p\)和\(q\)一直往上跳,直到两个指针的父节点相同。
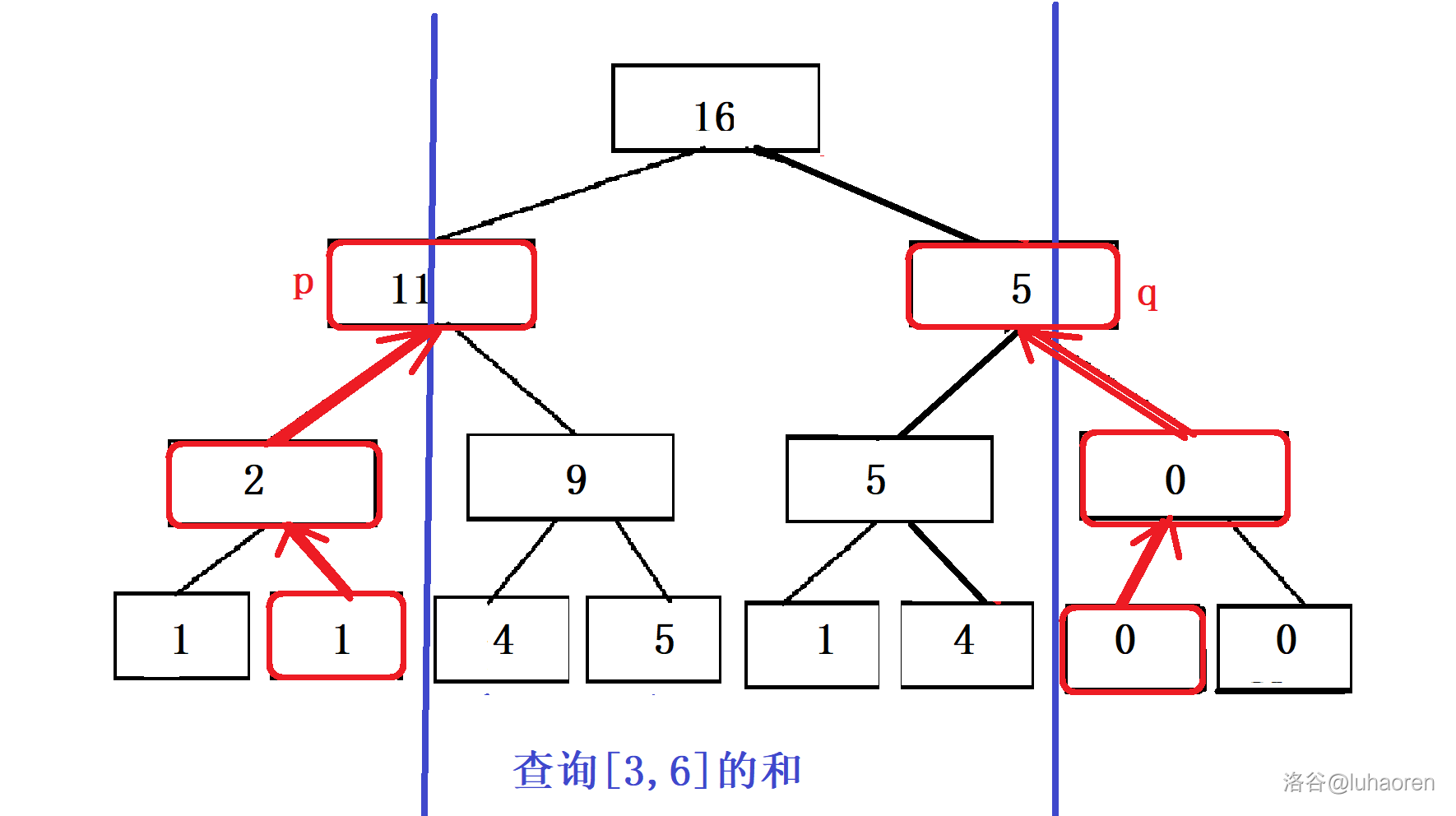
有没有发现,这两个指针笼罩的地方,就是我们要查询的区间。
多观察一会,我们会发现一个规律:
-
\(p\)指向的节点是左儿子,那么答案加上右儿子的值
-
\(q\)指向的节点是右儿子,那么答案加上左儿子的值
区间查询代码
inline int query(int l,int r){
int ans=0;
for(int p=l-1,q=r+1;p/2!=q/2;p/=2,q/=2){
if(!(p%2)) ans+=tr[p+1];//第一种情况
if(q%2) ans+=tr[q-1];//第二种情况
}
return ans;
}
习题
- P3374 单点修改,区间查询 用zkw线段树再做一遍
区间修改&单点查询
区间修改
zkw线段树也支持区间修改,但是由于很难做到pushdown,所以zkw线段树采用标记永久化的方式进行区间修改。
区间修改和区间查询差不多,也是维护两个指针,不同点是:从累加答案变成修改懒标记。
区间修改代码
void uplate(int l,int r,int k){//给l,r区间内的数加上k
for(int p=l-1,q=r+1;p/2!=q/2;p/=2,q/=2){
if(!(p%2)) add[p+1]+=k;
if(q%2) add[q-1]+=k;
}
}
单点查询
在有懒标记的情况下,单点查询也变得不同。
首先自底向上累加所有祖宗节点的懒标记,然后再加上本身的值。
单点查询代码
inline int query_one(int x){//查询x值
int sum=0;
for(int i=x+=n;i;i/=2) sum+=add[i];
return tr[x+n]+add[i];
}
习题
- P3372 线段树1
用zkw线段树做一遍 - P3368 树状数组2
区间修改,单点查询
可持久化线段树
可持久化线段树 ,顾名思义,就是可以保留每一个历史版本,并且支持在历史版本上进行操作的线段树。
为什么要可持久化呢?有的时候离线维护扫描线之类的东西时,就需要在时间轴里穿梭,这就需要历史版本;权值线段树如果能可持久化,就可以维护区间的数据,达到静态树套树的效果。
那么如何可持久化呢?
首先,最暴力的做法就是,开\(n\)个线段树,但是这样肯定会爆空间,所以,我们得想点别的招。
如图,这是一个普通的线段树。
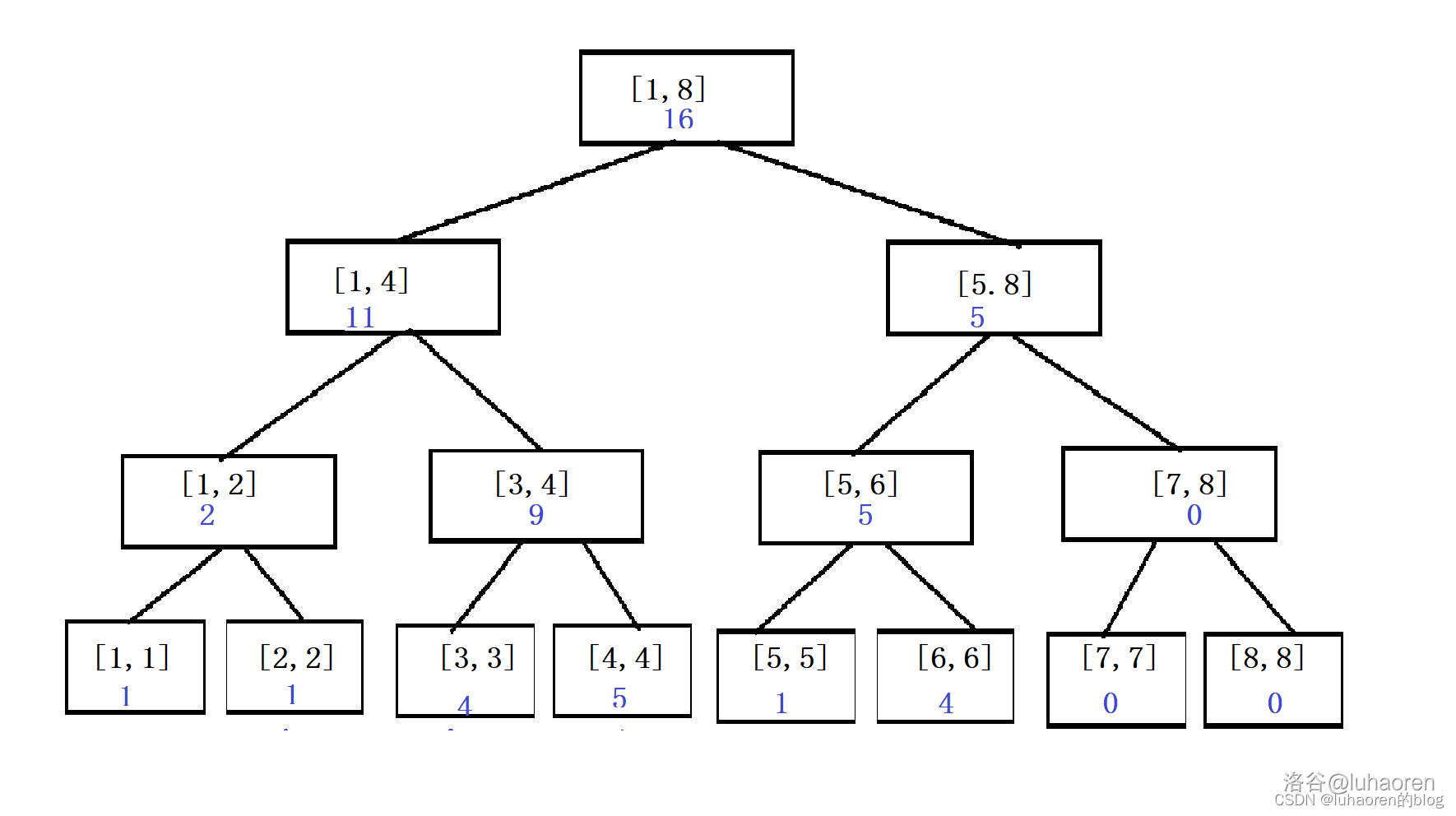
我们把第7个数加上3,如图。
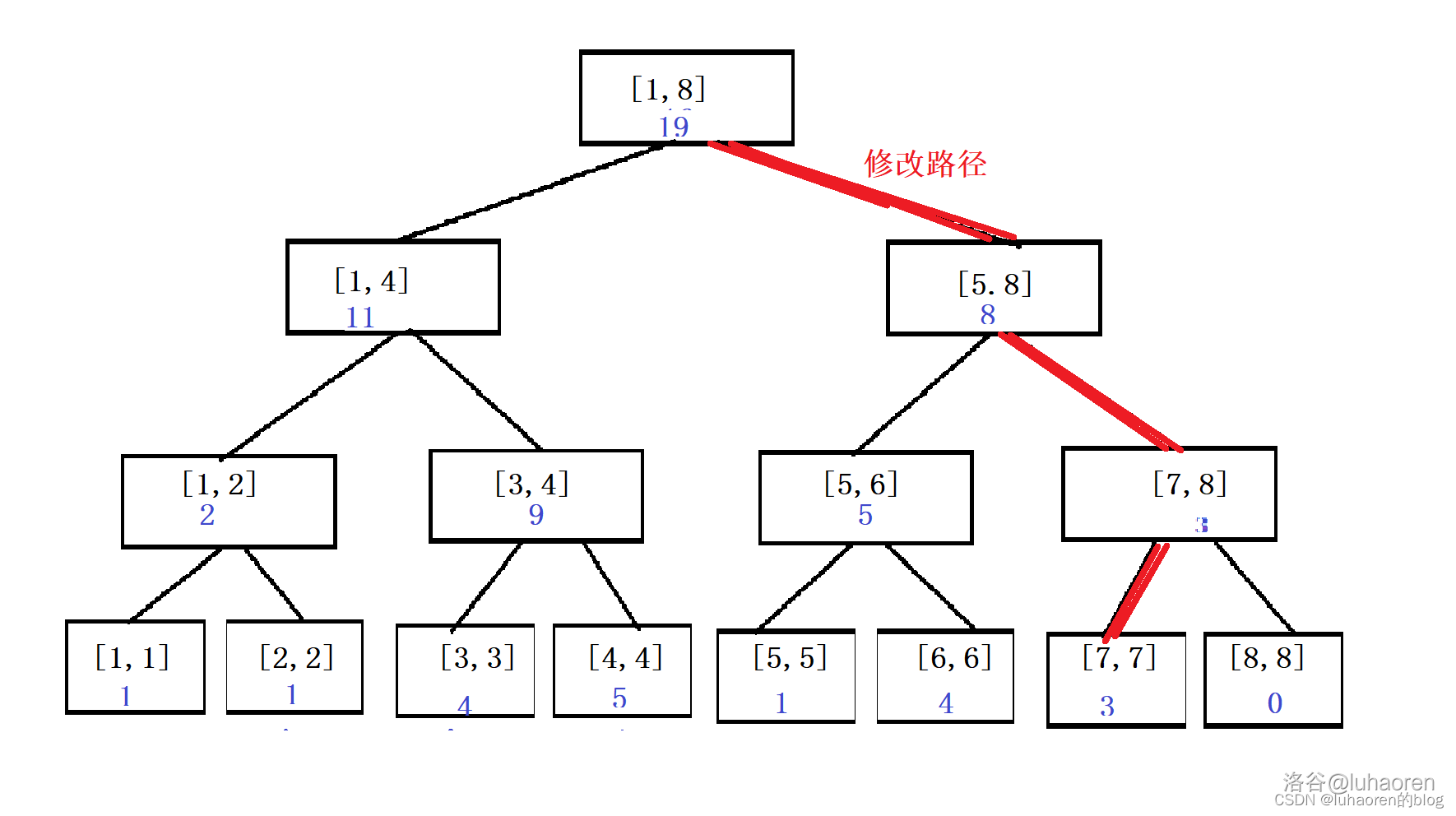
仔细观察,就会发现,被修改的节点实际上只是一条链,长度为\(\log n\)。
于是,著名神犇hjt突发奇想,如果每次修改只维护一条链的话,空间复杂度就变成\(O(n+m\log n)\)了呀。
于是就有了可持久化线段树,也叫主席树(能猜到原因吧)
如图,在可持久化线段树里给第7个数加上3。
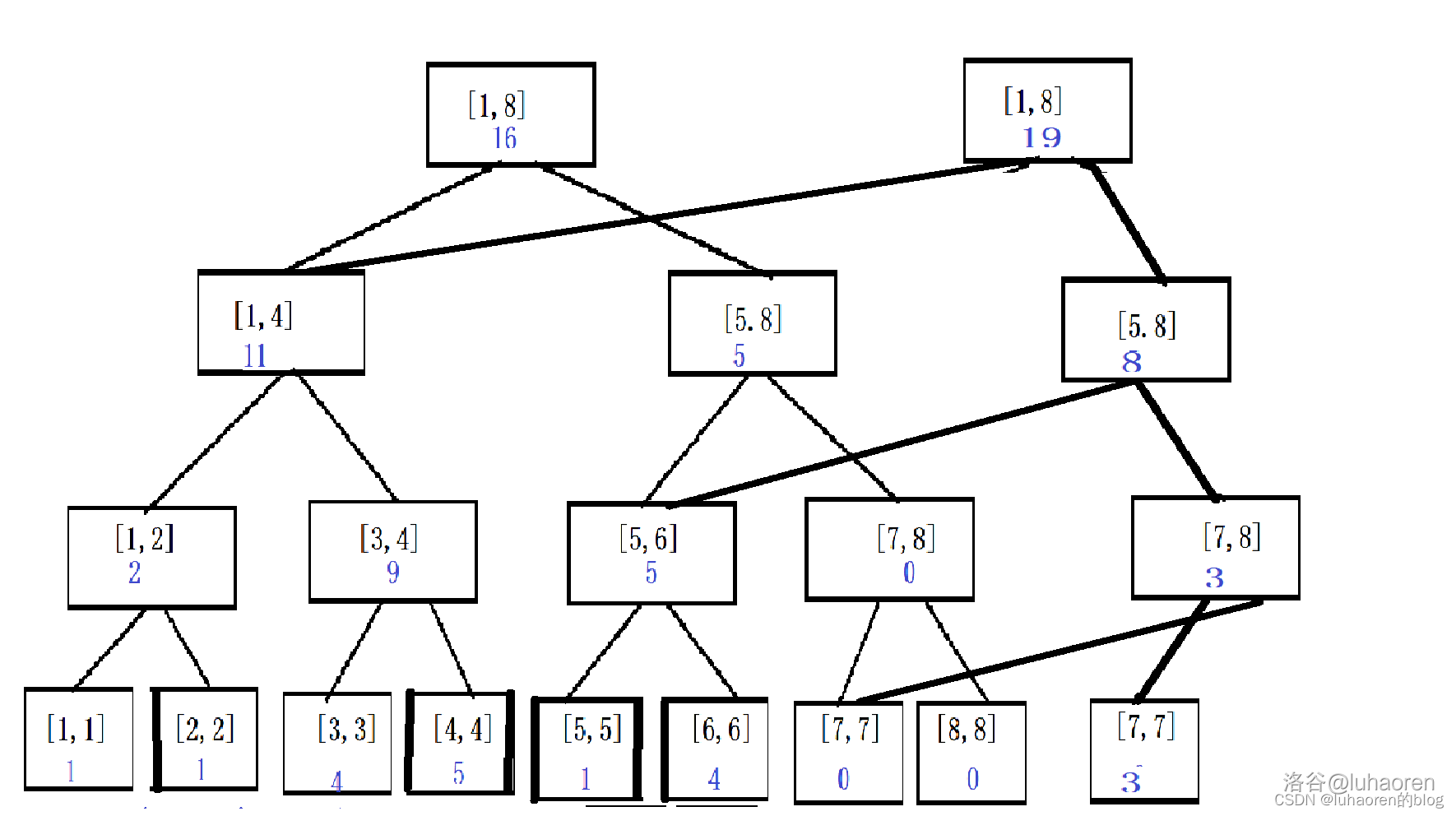
从这个图中,我们可以看出可持久化线段树的诀窍在于——复用历史版本的节点。
可持久化线段树只会增加需要修改的节点,而不需要修改的节点就可以使用以前的结构,这种思想被称为“函数式编程“,所以可持久化线段树也叫”函数式线段树“。
核心代码
void build(int &x,int l,int r){
//建树操作,即第0个版本,所有版本复用的基础
x=++tot;//可持久化线段树使用动态开点的方式,因此需要有lsrs数组存储左右儿子节点
if(l==r){
tr[x]=a[l];
return;
}
int mid=(l+r)/2;
build(ls[x],l,mid),build(rs[x],mid+1,r);
//因为x是引用形式,所以会直接给lsrs数组赋值
}
void change(int u,int &x,int l,int r,int k,int p){
x=++tot;
tr[x]=tr[u],ls[x]=ls[u],rs[x]=rs[u];
//复制原节点
if(l==r){
tr[x]=p;
return;
}
int mid=(l+r)/2;
if(k<=mid) change(ls[u],ls[x],l,mid,k,p);//修改左儿子,右儿子直接复用原节点的右儿子
else change(rs[u],rs[x],mid+1,r,k,p);//同理
}
例题6:可持久化数组
维护这样的一个长度为 \(N\) 的数组,支持如下几种操作:
- 在某个历史版本上修改某一个位置上的值
- 访问某个历史版本上的某一位置的值
此外,每进行一次操作(对于操作\(2\),即为生成一个完全一样的版本,不作任何改动),就会生成一个新的版本。版本编号即为当前操作的编号(从\(1\)开始编号,版本\(0\)表示初始状态数组)
题目分析
很明显,这一个可持久化线段树模板题,需要单点修改,单点查询,套用模板即可。
AC代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+10,M=5e7+10;//可持久化线段树大概需要O(4n+mlogn)的空间,一般直接开N<<5
int tr[M],root[N],ls[M],rs[M],tot=0,a[N];
void build(int &x,int l,int r){
x=++tot;
if(l==r){
tr[x]=a[l];
return;
}
int mid=(l+r)/2;
build(ls[x],l,mid),build(rs[x],mid+1,r);
}
void change(int u,int &x,int l,int r,int k,int p){
x=++tot;//动态开点
tr[x]=tr[u],ls[x]=ls[u],rs[x]=rs[u];//复制节点
if(l==r){
tr[x]=p;
return;
}
int mid=(l+r)/2;
if(k<=mid) change(ls[u],ls[x],l,mid,k,p);
else change(rs[u],rs[x],mid+1,r,k,p);
}
int query(int x,int l,int r,int k){
if(l==r) return tr[x];
int mid=(l+r)/2;
if(k<=mid) return query(ls[x],l,mid,k);
return query(rs[x],mid+1,r,k);
}
int n,m;
int main(){
scanf("%d%d",&n,&m);//本题稍微有点卡常,需要用printf和scanf
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
build(root[0],1,n);
for(int i=1;i<=m;i++){
int v,opt,k,p;
scanf("%d%d",&v,&opt);
if(opt==1){
scanf("%d%d",&k,&p);
change(root[v],root[i],1,n,k,p);
}
else{
scanf("%d",&k);
printf("%d\n",query(root[v],1,n,k));
root[i]=root[v];
}
}
}
例题7:静态区间第k小
给定\(n\) 个整数构成的序列 \(a\),将对于指定的闭区间 \([l,r]\) 查询其区间内的第 \(k\) 小值。
题目分析
如果没有区间操作,查询第k小可以用权值线段树实现,如果有要支持区间操作呢?
我们建一颗可持久化权值线段树,如图,把\(\{2,4,1,3\}\)这个数列的数依次插入。
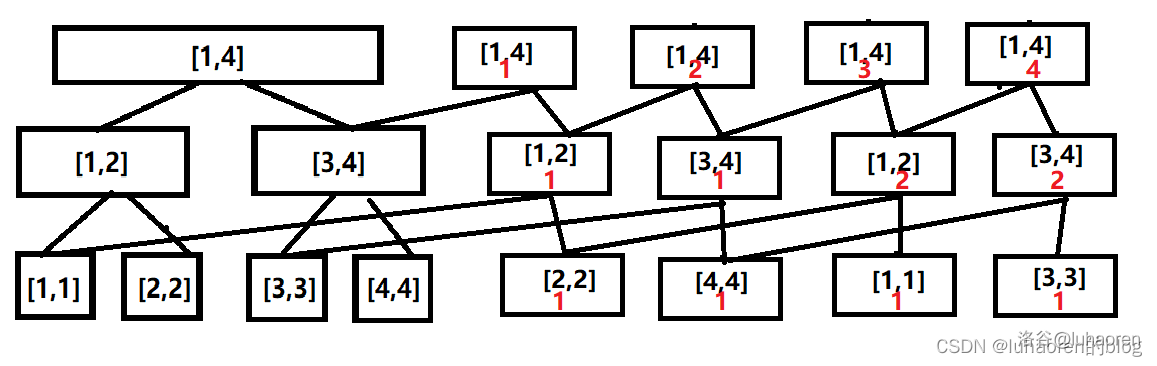
仔细观察,就会发现第\(i\)棵树保存着前\(i\)个数的信息(设初始化的树为第\(0\)棵)
也就是说,这个可持久化线段树可以说是数列的“前缀树”。
你能想到什么?
可持久化线段树满足区间可加减性,所以我们可以用前缀和的方式找出维护\([l,r]\)个数的信息的树。
也就是拿出第\(l-1\)棵树和第\(r\)棵树,两者相减,结果就是\([l,r]\)的信息。
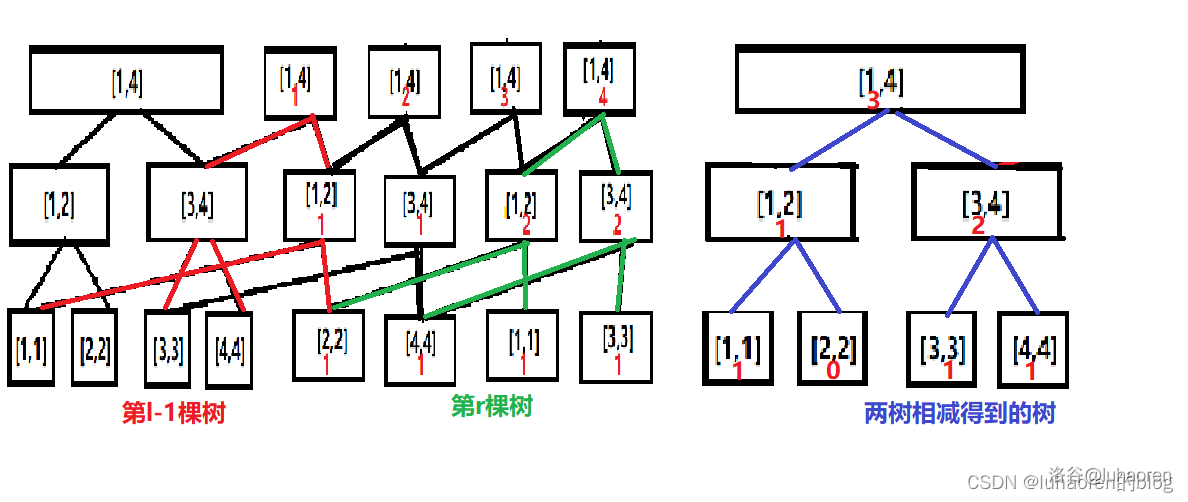
而在相减后的树上找第k小相信大家都已经会了。
那么就可以写出代码了!
注:这题数据很水,题面给\(|a_i |\le 10^9\),但实际上的数据范围是\(0 \le a_i \le 10^6\),甚至不需要离散化的优化,就可以过。
AC代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int tr[N<<5],ls[N<<5],rs[N<<5],root[N],tot=0;
void build(int &x,int l,int r){
//建树
x=++tot;
if(l==r) return;
int mid=(l+r)/2;
build(ls[x],l,mid),build(rs[x],mid+1,r);
}
void insert(int u,int &x,int l,int r,int k){
x=++tot;//动态开点
tr[x]=tr[u]+1,ls[x]=ls[u],rs[x]=rs[u];//复制该节点的所有信息(可以直接在节点上+1,否则还得pushuo一遍)
if(l==r) return;
int mid=(l+r)/2;
if(k<=mid) insert(ls[u],ls[x],l,mid,k);
else insert(rs[u],rs[x],mid+1,r,k);
}
int query(int u,int v,int l,int r,int k){
int mid=(l+r)/2,lx=tr[ls[v]]-tr[ls[u]];//两颗树信息相减得到的左儿子信息
if(l==r) return l;//如果只有一个数,第几大都是这个数了,直接返回
if(k<=lx) return query(ls[u],ls[v],l,mid,k);
return query(rs[u],rs[v],mid+1,r,k-lx);//二分查找第k小
}
int n,m;
int main(){
cin>>n>>m;
build(root[0],0,1e6);//建树
for(int i=1;i<=n;i++){
int t;
cin>>t;
insert(root[i-1],root[i],0,1e6,t);
}
while(m--){
int l,r,k;
cin>>l>>r>>k;
cout<<query(root[l-1],root[r],0,1e6,k)<<endl;
}
}
实际上,这份代码在除了洛谷以外的其它OJ上是AC不了的,因为题面上\(|a_i|\le 10^9\)的数据范围使代码必须要有离散化的优化,这里给出优化代码。
//其他部分和前面无异,这以后是离散化代码
int n,m,tt=0;
map<int,int>mp;//使用map离散化,使用sort离散化也可以
int val[N],a[N];
int main(){
cin>>n>>m;
build(root[0],1,n);
for(int i=1;i<=n;i++){
cin>>a[i];
mp[a[i]]=0;
}
for(auto it:mp){
//map会自己排序,在遍历的过程中标上映射后的序号
mp[it.first]=++tt;
val[tt]=it.first;
}
for(int i=1;i<=n;i++) insert(root[i-1],root[i],1,n,mp[a[i]]);
while(m--){
int l,r,k;
cin>>l>>r>>k;
cout<<val[query(root[l-1],root[r],1,n,k)]<<endl;
}
}
习题
- 洛谷P3402 可持久化并查集
注意并查集的合并操作 - [POI2014] KUR-Couriers
维护区间绝对众数,有乱搞做法
U.P.D
2023年2月17日 初稿,大概两千多字。
2023年6月? cry拿去学,发现了一堆错误(比如代码写了个tr[x]=tr[x*2]+tr[x*2])。
2023年7月3日 开始重写。
2023年7月6日 写完基础部分
2023年7月8日 增加了权值线段树
2023年7月9日 挪到了洛谷上,把图片传到了洛谷图床上。增加了权值线段树的习题。
2023年7月9日 增加了zkw线段树
2023年7月11日 增加了可持久化线段树




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】