第五课第四周实验一：Embedding_plus_Positional_encoding 嵌入向量加入位置编码

变压器预处理

变压器预处理

欢迎来到第 4 周的第一个未分级实验室。在本笔记本中，您将深入研究应用于原始文本的预处理方法，然后再将其传递给转换器架构的编码器和解码器块。

完成这项任务后，您将能够：

创建可视化以获得对位置编码的直觉
可视化位置编码如何影响词嵌入

包

运行以下单元格以加载您需要的包。

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import os

from tensorflow.keras.layers import Embedding
from tensorflow.keras.preprocessing.text import Tokenizer
from tensorflow.keras.preprocessing.sequence import pad_sequences

1 - 位置编码

以下是您在上一个作业中实现的位置编码方程。此编码使用以下公式：

\[PE_{(pos, 2i)}= sin\left(\frac{pos}{{10000}^{\frac{2i}{d}}}\right) \]

$$ PE_{(pos, 2i+1)}= cos\left(\frac{pos}{{10000}^{\frac{2i}{d}}}\right) $$

在将文本输入语言模型之前，将句子转换为标记是自然语言处理任务中的标准做法。然后将每个标记转换为固定长度的数字向量，称为嵌入，它捕获单词的含义。在 Transformer 架构中，位置编码向量被添加到嵌入中以在整个模型中传递位置信息。
仅通过检查数字表示可能难以掌握这些向量的含义，但可视化有助于直观了解单词的语义和位置相似性。正如您在之前的作业中看到的那样，当嵌入被缩减为二维并绘制时，语义相似的词看起来更靠近，而不同的词则被绘制得更远。可以使用位置编码向量进行类似的练习 - 在笛卡尔平面上绘制时，句子中距离较近的单词应该看起来更近，而在句子中距离更远时，应该在平面上出现更远。
在本笔记本中，您将创建一系列词嵌入和位置编码向量的可视化，以直观了解位置编码如何影响词嵌入并帮助通过 Transformer 架构传输顺序信息。

1.1 - 位置编码可视化

以下代码单元格具有您在 Transformer 赋值中实现的 positional_encoding 函数。干得好！您将利用此笔记本中的此功能构建更多的可视化效果。

def positional_encoding(positions, d):
    """
    预先计算所有位置编码的矩阵
    
   参数：
         position (int) -- 要编码的最大位置数
         d (int) -- 编码大小
    
    返回：
         pos_encoding -- (1, position, d_model) 带有位置编码的矩阵
    """

    # 初始化所有角度的矩阵angle_rads
    angle_rads = np.arange(positions)[:, np.newaxis] / np.power(10000, (2 * (np.arange(d)[np.newaxis, :]//2)) / np.float32(d))
    angle_rads[:, 0::2] = np.sin(angle_rads[:, 0::2])
    angle_rads[:, 1::2] = np.cos(angle_rads[:, 1::2])
    
    pos_encoding = angle_rads[np.newaxis, ...]
    
    return tf.cast(pos_encoding, dtype=tf.float32)

将嵌入维度定义为 100。该值必须与词嵌入的维度匹配。在 "Attention is All You Need" 论文中，嵌入大小从 100 到 1024 不等，具体取决于任务。作者还根据任务使用了从 40 到 512 不等的最大序列长度。定义最大序列长度为 100，最大字数为 64。

EMBEDDING_DIM = 100
MAX_SEQUENCE_LENGTH = 100
MAX_NB_WORDS = 64
pos_encoding = positional_encoding(MAX_SEQUENCE_LENGTH, EMBEDDING_DIM)

plt.pcolormesh(pos_encoding[0], cmap='RdBu')
plt.xlabel('d')
plt.xlim((0, EMBEDDING_DIM))
plt.ylabel('Position')
plt.colorbar()
plt.show()

你已经在这个作业中创建了这个可视化，但让我们深入一点。注意矩阵的一些有趣的特性——第一个是每个向量的范数总是一个常数。无论 pos 的值是多少，范数将始终是相同的值，在本例中为 7.071068。从这个属性你可以得出结论，两个位置编码向量的点积不受向量尺度的影响，这对相关计算有重要意义。

pos = 34
tf.norm(pos_encoding[0,pos,:])


输出:<tf.Tensor: shape=(), dtype=float32, numpy=7.071068>

另一个有趣的特性是由k 个位置分隔的 2 个向量之间的差异的范数也是常数。如果您保持 k 不变并更改 pos，则差异将大致相同。这个属性很重要，因为它表明差异不取决于每个编码的位置，而是取决于编码之间的相对分离。能够将位置编码表示为彼此的线性函数，可以帮助模型通过关注单词的相对位置来学习。

这种用向量编码来反映词的位置差异是很难实现的，特别是考虑到向量编码的值必须保持足够小，以便它们不会扭曲词嵌入。

pos = 70
k = 2
print(tf.norm(pos_encoding[0,pos,:] -  pos_encoding[0,pos + k,:]))
输出：tf.Tensor(3.2668781, shape=(), dtype=float32)

您已经观察到了一些关于位置编码向量的有趣属性——接下来，您将创建一些可视化，看看这些属性如何影响编码和嵌入之间的关系！

1.2 - 比较位置编码

1.2.1 - 相关性

位置编码矩阵有助于可视化每个向量对于每个位置的唯一性。但是，目前还不清楚这些向量如何表示句子中单词的相对位置。为了说明这一点，您将计算每个位置的向量对之间的相关性。一个成功的位置编码器将产生一个完美对称的矩阵，其中最大值位于主对角线上——相似位置的向量应该具有最高的相关性。按照相同的逻辑，相关值应该随着远离主对角线而变小。

# 位置编码相关
corr = tf.matmul(pos_encoding, pos_encoding, transpose_b=True).numpy()[0]
plt.pcolormesh(corr, cmap='RdBu')
plt.xlabel('Position')
plt.xlim((0, MAX_SEQUENCE_LENGTH))
plt.ylabel('Position')
plt.colorbar()
plt.show()

1.2.2 - 欧几里得距离

您还可以使用欧几里德距离而不是相关性来比较位置编码向量。在这种情况下，您的可视化将显示一个矩阵，其中主对角线为 0，并且其非对角线值随着它们远离主对角线而增加。

# Positional encoding euclidean distance
eu = np.zeros((MAX_SEQUENCE_LENGTH, MAX_SEQUENCE_LENGTH))
print(eu.shape)
for a in range(MAX_SEQUENCE_LENGTH):
    for b in range(a + 1, MAX_SEQUENCE_LENGTH):
        eu[a, b] = tf.norm(tf.math.subtract(pos_encoding[0, a], pos_encoding[0, b]))
        eu[b, a] = eu[a, b]
        
plt.pcolormesh(eu, cmap='RdBu')
plt.xlabel('Position')
plt.xlim((0, MAX_SEQUENCE_LENGTH))
plt.ylabel('Position')
plt.colorbar()
plt.show()

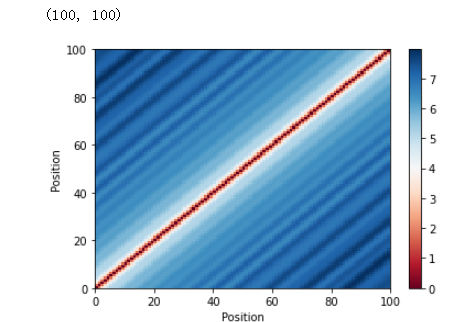
干得好！您可以使用这些可视化来检查您创建的任何位置编码。

2 - 语义嵌入

通过创建相关矩阵和距离矩阵，您已经深入了解位置编码向量与不同位置的其他向量之间的关系。类似地，通过可视化这些向量的总和，您可以更直观地了解位置编码如何影响词嵌入。

2.1 - 加载预训练嵌入

要将预训练的词嵌入与您创建的位置编码相结合，请首先从 glove 项目加载预训练的嵌入之一。您将使用具有 100 个特征的嵌入。

embeddings_index = {}
GLOVE_DIR = "glove"
f = open(os.path.join(GLOVE_DIR, 'glove.6B.100d.txt'))
for line in f:
    values = line.split()
    word = values[0]
    coefs = np.asarray(values[1:], dtype='float32')
    embeddings_index[word] = coefs
f.close()

print('Found %s word vectors.' % len(embeddings_index))
print('d_model: %s', embeddings_index['hi'].shape)
输出：Found 400000 word vectors.
      d_model: %s (100,)

注意： 这个嵌入由 400,000 个词组成，每个词嵌入有 100 个特征。

考虑以下仅包含两个句子的文本。等一下 - 这些句子没有意义！相反，这些句子被设计为：

每个句子由词组组成，词组之间有一定的语义相似性。
第一句中相似词是连续的，而在第二句中，顺序是随机的。

texts = ['king queen man woman dog wolf football basketball red green yellow',
         'man queen yellow basketball green dog  woman football  king red wolf']

首先，运行以下代码单元以将标记化应用于原始文本。不要太担心这一步的作用 - 将在以后的未分级实验中详细解释。快速总结（对于理解实验室并不重要）：

如果你输入一个不同句子长度的纯文本数组，它将为每个句子生成一个矩阵，每个句子由一个大小为MAX_SEQUENCE_LENGTH的数组表示。
此数组中的每个值使用字典中的相应索引（word_index）表示句子中的每个单词。
短于MAX_SEQUENCE_LENGTH 的序列用零填充以创建统一长度。

同样，这将在以后的未分级实验中详细解释，所以现在不要太担心！

tokenizer = Tokenizer(num_words=MAX_NB_WORDS)
tokenizer.fit_on_texts(texts)
sequences = tokenizer.texts_to_sequences(texts)

word_index = tokenizer.word_index
print('Found %s unique tokens.' % len(word_index))

data = pad_sequences(sequences, padding='post', maxlen=MAX_SEQUENCE_LENGTH)

print(data.shape)

print(data)

为了简化您的模型，您只需要获取您正在检查的文本中出现的不同单词的嵌入。在这种情况下，您将仅过滤掉出现在我们句子中的 11 个单词。第一个向量将是一个零数组，并将编码所有未知单词。

embedding_matrix = np.zeros((len(word_index) + 1, EMBEDDING_DIM))
for word, i in word_index.items():
    embedding_vector = embeddings_index.get(word)
    if embedding_vector is not None:
        # words not found in embedding index will be all-zeros.
        embedding_matrix[i] = embedding_vector
print(embedding_matrix.shape)
输出：(12, 100)

使用从预训练手套嵌入中提取的权重创建嵌入层。

embedding_layer = Embedding(len(word_index) + 1,
                            EMBEDDING_DIM,
                            embeddings_initializer=tf.keras.initializers.Constant(embedding_matrix),
                            trainable=False)

使用前一层将输入标记化数据转换为嵌入。检查嵌入的形状以确保该矩阵的最后一个维度包含句子中单词的嵌入。

embedding = embedding_layer(data)
print(embedding.shape)
输出：(2, 100, 100)

2.2 - 笛卡尔平面上的可视化

现在，您将创建一个函数，允许您在笛卡尔平面中可视化我们的单词编码。您将使用 PCA 将手套嵌入的 100 个特征减少到仅 2 个组件。

from sklearn.decomposition import PCA

def plot_words(embedding, sequences, sentence):
    pca = PCA(n_components=2)
    X_pca_train = pca.fit_transform(embedding[sentence,0:len(sequences[sentence]),:])


    fig, ax = plt.subplots(figsize=(12, 6)) 
    plt.rcParams['font.size'] = '12'
    ax.scatter(X_pca_train[:, 0], X_pca_train[:, 1])
    words = list(word_index.keys())
    for i, index in enumerate(sequences[sentence]):
        ax.annotate(words[index-1], (X_pca_train[i, 0], X_pca_train[i, 1]))

好的！现在您可以绘制每个句子的嵌入。每个图都应该显示不同单词的嵌入。

plot_words(embedding, sequences, 0)

绘制第二个句子的词嵌入。回想一下，第二个句子包含与第一个句子相同的单词，只是顺序不同。您可以看到单词的顺序不会影响向量表示。

plot_words(embedding, sequences, 1)

3 - 语义和位置嵌入

接下来，您将原始手套嵌入与您之前计算的位置编码相结合。在本练习中，您将在语义嵌入和位置嵌入之间使用 1 比 1 的权重比。

embedding2 = embedding * 1.0 + pos_encoding[:,:,:] * 1.0

plot_words(embedding2, sequences, 0)
plot_words(embedding2, sequences, 1)

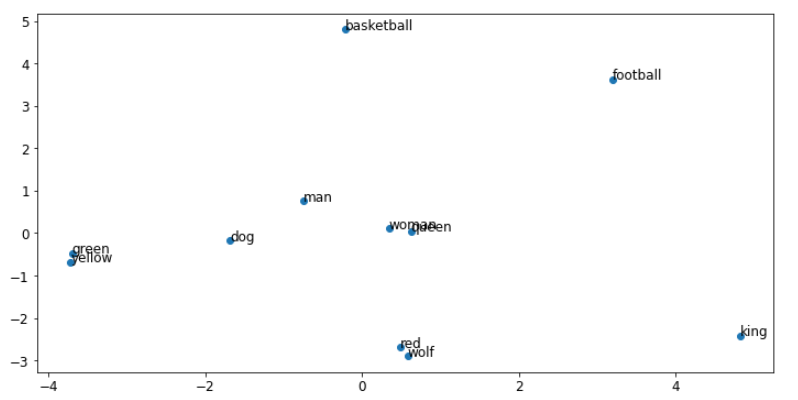
哇看看情节之间的巨大差异！与原始对应物相比，这两个地块都发生了巨大变化。请注意，在第二个图像中，对应于相似词不在一起的句子，非常不同的词（如 red 和 wolf）显得更接近。

现在您可以尝试不同的相对权重，看看这如何强烈影响句子中单词的向量表示。

W1 = 1 # Change me
W2 = 10 # Change me
embedding2 = embedding * W1 + pos_encoding[:,:,:] * W2
plot_words(embedding2, sequences, 0)
plot_words(embedding2, sequences, 1)

# For reference
#['king queen man woman dog wolf football basketball red green yellow',
# 'man queen yellow basketball green dog  woman football  king red wolf']

如果你设置W1 = 1和W2 = 10，你可以看到单词的排列是如何根据单词在句子中的位置开始呈顺时针或逆时针顺序的。在这些参数下，位置编码向量主导了嵌入。

现在尝试将权重反转为“W1 = 10”和“W2 = 1”。观察到在这些参数下，绘图类似于原始嵌入可视化，并且绘制的单词位置之间只有很少的变化。

在之前的 Transformer 赋值中，词嵌入乘以 sqrt(EMBEDDING_DIM)。在这种情况下，使用 W1 = sqrt(EMBEDDING_DIM) = 10 和 W2 = 1 将是等效的。

恭喜！

您已经完成了本笔记本，并且对 Transformer 网络的输入有了更好的了解！

到目前为止，您已经：

创建位置编码矩阵来可视化向量的关系属性
在笛卡尔平面上绘制嵌入和位置编码以观察它们如何相互影响

你应该记住的：

位置编码可以表示为彼此的线性函数，允许模型根据单词的相对位置进行学习。
位置编码会影响词嵌入，但如果位置编码的相对权重较小，则总和将保留词的语义。

posted @ 2021-09-19 15:57 xingye_z 阅读(507) 评论(0) 编辑收藏举报

刷新页面返回顶部