n皇后编程问题

n皇后编程问题是一个经典问题，记得2018年北京航空航天大学计算机学院的博士招聘的上机题目就是这个，这里给出几种实现方法：

import time
import itertools

Num =  8
# Num = 12   # 8

def f1():
    def test_queens(queens):
        for x in range(Num):
            for y in range(x+1, Num):
                if abs(queens[x]-queens[y])==abs(x-y):
                    return False
        return True
    
    counter = 0
    for i in range(12345678, 87654321, 1):
        s = str(i)
        if "0" in s or "9" in s:
            continue
        if len(set(s)) != 8:
            continue
        if test_queens([int(digit)-1 for digit in s]):
            counter += 1
    return counter


def f2():
    def conflict(state, nextX):
        nextY = len(state)
        for i in range(nextY):
            if abs(state[i]-nextX) in (0, nextY-i):
                return True
        return False

    def queens(num=Num, state=()):
        for pos in range(num):
            if not conflict(state, pos):
                if len(state) == num-1:
                    yield (pos, )
                else:
                    for result in queens(num, state+(pos, )):
                        yield (pos, ) + result

    return queens()


def f3():
    num = Num
    def conflict(queen):
        for x in range(num):
            for y in range(x+1, num):
                if abs(queen[x]-queen[y])==(y-x):
                    return True
        return False

    queens = []
    for queen in itertools.permutations(range(num)):
        if not conflict(queen):
            queens.append(queen)
    return queens


_a = time.time()
print(f1())
_b = time.time()
print(_b - _a)


_a = time.time()
print(len([x for x in f2()]))
_b = time.time()
print(_b - _a)


_a = time.time()
print(len([x for x in f3()]))
_b = time.time()
print(_b - _a)

上面的实现中，当n=8时，f1()函数实现、f2()函数实现、f3()函数实现的运行时间如下（单位为秒）：

92
11.19756269454956
92
0.005673408508300781
92
0.019522428512573242

可以看到f1()函数的实现是f2实现的2000倍的用时，因此在下面的n=12时我们只给出f2()和f3()函数实现下的用时：

14200
4.591862201690674
14200
295.7449884414673

可以看到，f3()的实现下用时是f2()实现下的60倍。

总结：

f2()方法实现是运行时间最短的方法。

f3()方法是f2()用时的60倍。

f1()方法是f2()用时的2000倍。

不过在n=8时，也就是8皇后问题下，f2()和f3()的用时都是符合一般要求的（1秒以内或5秒以内）。

由于f2()中使用了yield，这一点并不通用，于是将其改为return，并加入sss=[ ]作为状态保存，具体代码如下：

import time
import itertools
 
Num =  8

 
def f2():
    def conflict(state, nextX):
        nextY = len(state)
        for i in range(nextY):
            if abs(state[i]-nextX) in (0, nextY-i):
                return True
        return False
 
    def queens(num, state=()):
        sss = []
        for pos in range(num):
            if not conflict(state, pos):
                if len(state) == num-1:
                    # yield (pos, )
                    sss.append((pos,))
                else:
                    for result in queens(num, state+(pos, )):
                        # yield (pos, ) + result
                        sss.append( (pos, ) + result )
        return sss

    return queens(8)
 
_a = time.time()
print(len([x for x in f2()]))
_b = time.time()
print(_b - _a)

运行结果如下：

不过考虑到即使把f2()中的yield改为return也是需要使用递归算法的，而递归算法是可以使用循环算法来替代的，于是使用循环算法修改f2()中的递归，得到如下代码：

import time
 
 
def f2():
    def conflict(state, nextX):
        nextY = len(state)
        for i in range(nextY):
            if abs(state[i]-nextX) in (0, nextY-i):
                return True
        return False
 
    def queens():
        s = [[i, ] for i in range(8)]  # 初始化
        s_tmp = []

        count = 0

        while count<8-1:
            for state in s:
                for pos in range(8):
                    if not conflict(state, pos):
                        state_copy = state.copy()
                        state_copy.append(pos)
                        s_tmp.append(state_copy)
            s = s_tmp
            s_tmp = []
            count += 1
        return s

    return queens()
 
_a = time.time()
print(len([x for x in f2()]))
_b = time.time()
print(_b - _a)

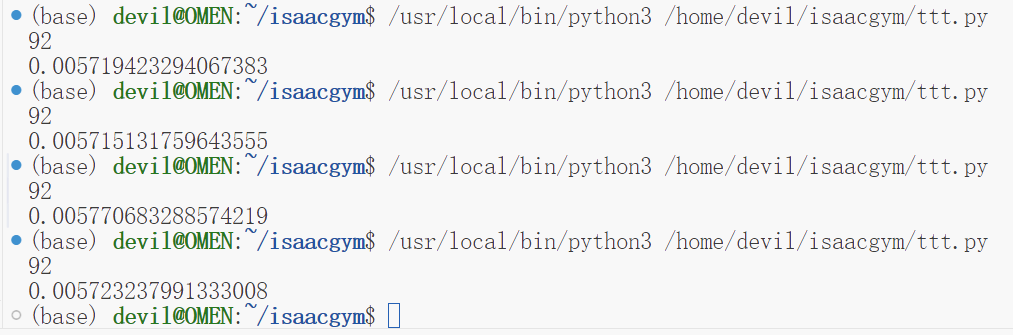
运行结果如下：

个人github博客地址：
https://devilmaycry812839668.github.io/