机器学习领域中置信区间的使用

首先说明一下，置信区间和假设检验都是数理统计中的方法，这两种方法在机器学习领域主要用作对实验结果的可信度评估上。

 

PS: 置信区间与假设检验在原理上是相通的。

 

基本概念：

样本（一般指样本集合）：一次从总体抽样中获得的样本集合。

样本量/样本个数：一次从总体抽样中获得的样本集合的样本数目。

抽样个数（一般指放回抽样）：总共从总体中抽取样本的次数，每次抽取的都是一个样本集合。
 
 

---------------------------------------------------

 

 

置信区间

计算置信区间的方法有很多种，本文只讲最基础的方法。

注意：置信区间在机器学习领域使用的并不多，而且很多paper中的使用方法存在不恰当的问题。

 

之前已经分享过置信区间的讲解文章：

https://www.cnblogs.com/devilmaycry812839668/p/15638870.html

从上面这个文章可以知道最简单形式的置信区间估计的具体计算方法，也就是说根据中心极限定理来进行构造的，根据（下面的推导过程也引用自该链接）https://wenku.baidu.com/view/0ab2b4aa1ae8b8f67c1cfad6195f312b3169eb24?aggId=0ab2b4aa1ae8b8f67c1cfad6195f312b3169eb24&_wkts_=1670288469210&bdQuery=%E7%BD%AE%E4%BF%A1%E5%8C%BA%E9%97%B4%28%E8%AF%A6%E7%BB%86%E5%AE%9A%E4%B9%89%E5%8F%8A%E8%AE%A1%E7%AE%97%29

 

可以知道具体的推到过程，这里再次给出大致的推导过程：

随机变量服从某个分布（该分布的具体形式可以不知道），现在对该分布进行抽样，抽样样本量为n，样本的均值为X_bar，这里需要注意的是样本的均值X_bar依然是随机变量，X_bar=(X1+X2+...+Xn)/n，X_bar的统计量：

 

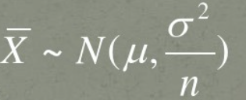
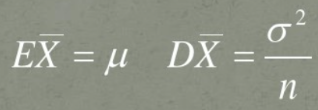
根据X_bar及其统计量可以构造成新的随机变量Z，具体形式： 

  

Z的1-α置信区间的表示为：

  

 

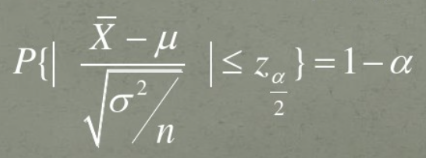
这里我们就已经获得了最简单形式的置信区间，这里X_bar已经通过采样获得，n为已知数值，唯一没有获得σ为原分布的方差，即随机变量X的方差。

由于很多时候X的方差是未知的切无法获得，因此我们这里使用点估计来估计σ，也就是用样本方差来估计σ值，所以最终的表示形式可以写作：

计算置信区间：

a = 样本均值 - z*样本标准误差
b = 样本均值 + z*样本标准误差

最后置信区间就为 [a,b]，z值为标准正态分布的z值，样本的标准误差：sqrt_root(样本方差/n) .

这里是用X的样本方差来点估计X的总体方差。

 

上面的内容就是最基础的置信区间的计算，不过网上也有一些关于T 分布来计算置信区间的内容，如：https://www.cnblogs.com/devilmaycry812839668/p/15639544.html

以前没有系统规整过，其实很多关于该方式的介绍是存在问题的（包括上面链接），使用T分布的适用条件：

1. 总体分布为正态分布，即X服从正态分布；

2. 主要用于样本含量较小（例如n < 30）；

3. 总体标准差σ，即X的方差未知；

网上的资料说的一般只要样本量较小就使用T分布检验是不恰当的，这时主要的考虑因素是到底样本量对估计的影响占比大，还是原分布与正态分布的便宜对估计的影响大。如果样本量小于30，并且原分布近似于正态分布，或者比较贴近于正态分布，那么适合使用T分布；但是即使样本量小于30，但是总体分布与正太分布差异较大，那么也不适用T分布来估计置信区间，而是使用上面介绍的内容来估计。

(t分布的置信区间计算方式与上面的正态分布的自信区间计算方式在形式上很相似）

t 分布的置信区间：

计算置信区间：

a = 样本均值 - t*样本标准误差
b = 样本均值 + t*样本标准误差

最后置信区间就为 [a,b]，t值为自由度n-1下的t分布的t值，即t(n-1)，样本的标准误差：sqrt_root(样本方差/n) .

这里是用X的样本方差来点估计X的总体方差；由于样本量为n，因此t分布中的自由度为n-1.

 

需要注意的是在大多数情况下不特殊说明，分布都是默认为正太分布或近似于正太分布的，因此在没有特殊说明总体分布是与正太分布差距较大的情况下对于样本量较小时都是可以默认使用T分布估计置信区间的。

 

PS：为啥不知道分布的情况下都是默认为正太分布呢？ 

答：该问题目前学术界依然没有公认的答案，用人话来说就是还没有答案，为啥自然界中大部分的分布都是正态分布这个问题难以有大家认同的答案，也就是说自然界中大部分分布都是正态分布作为一个事实结果或许难以有答案，大家就把这个当做默认已知条件即可。不过依旧给出一些网友的观点来开阔思路：

以下节选自：https://blog.sciencenet.cn/blog-481915-390307.html

其实，自然条件下由于受众多因素影响，变量的分布不会是均匀分布。既然不是均匀分布，就会出现变量值的相对集中，变量就可能会呈现如正态分布那样的单峰分布。其实我们的疑问更多是为什么大多数变量会集中在“那个值”附近，以及为什么是单峰而不是多峰分布？对于第一个疑问，要具体问题具体分析。打个比方，假设北京市建筑物的高度70%集中在50-100m之间，为什么会是50-100m这个和北京市的社会经济发展水平、人口数量及地质条件等因素有关。也就是说变量所处的外部环境因素决定了变量值的集中范围。对于第二个疑问，为什么不是多峰。这可能也是由变量所处的外部环境决定。如果外部环境处于相对稳定的状态，那么其分布就不会是多峰型。而如果其外部环境经常变化，则其分布就可能是多峰型。以我所研究的土壤水分为例，土壤水分主要受降水和蒸发都因素的影响。由于一个地区的降雨量和蒸散发在一直变化，且有时候变化剧烈，导致土壤水分的概率分布呈现多峰（图2）。这种解释我个人觉得比较合理。但是主观性比较强，如果要更客观地去解释这种现象，还需要提出某种比较合理的理论。我希望借此抛砖引玉，和感兴趣的网友进行交流。

 

节选自：https://www.zhihu.com/question/26854682 

高尔顿钉板的装置，展示了正态分布的产生过程。

 

PS: 个人胡乱想法，自然界中事物性能受N多个因素影响，每个因素对事物的影响往往都是A、B两面的，并且概率都是相近为0.5的，这些因素对事物的影响累加后就像高尔顿钉板那样就把事物形成了类似正太分布的形式。

 

======================================

 

 

关于置信区间的正确解释：

（参考：https://www.zhihu.com/question/26419030/answer/70589735，作者：管致远）

首先要知道上面介绍的内容的是置信区间是对总体期望的估计，而总体的期望不是随机变量而是一个固定的真实值，只不过这个固定的真实值的大小还不清楚，但是这个数值是不会变化的（固定的）；不同于随机变量，我们不能说固定的真实值在某区间的概率为多少，我们只能说某个随机变量在某区间发生的概率为多少，真实的已经存在的数值是不能用概率来描述的，因此用“总体期望在置信区间的概率为置信度”的说法是不正确的（学术用语严谨性上的问题），正确的表述应该是“如果我们重复取样，每次抽样后都用这个方法构造置信区间，有 95% 的置信区间会包含总体期望”。

 

节选https://www.zhihu.com/question/26419030/answer/70589735部分内容：（作者：管致远）

换种方法说，假设我们还没有取样，但已经制定好取样后构造 95% 置信区间的方法。我们可以说取样一次以后，获得的那个置信区间（现在还不知道）包含真值的概率是 95%。然而在取样并得到具体的一个区间之后，在频率学派框架下就无法讨论这个区间包含真值的概率了。

取样前能讨论，取样后却无法讨论，这可能让很多人感到很不自然。扩大来说，传统频率学派对已经发生，但我们不知道结果的事件的讨论存在困难。虽然这个问题通常在应用上无伤大雅，但确实有不少学者因此寻求对概率的不同解释。

 

______________________

 

 

置信区间使用上的一些误区： 

在机器学习论文上经常看到一种使用置信区间的方法，如做了15次试验获得了15个结果，然后根据这15个数值计算出95%下的置信区间，然后根据这15个数值是否在这个置信区间之内来判断这15个试验结果是否具有统计特性，其实这是一种十分错误的使用方法。首先我们需要清楚置信区间、置信度都是对总体期望而言的，置信区间是指置信度下对总体期望覆盖的区间估计，我们可以通过这个区间来估计总体期望存在的大致位置，但是这个区间不能用来评估总体中的某样本如何；而且即使是两个分布的置信区间往往也不能进行比较，我们还能说根据两个分布的置信区间就能评价出一个分布的总体均值一定会比另一个好，除非是那种两个分布的置信区间没有重叠的情况，比如下面的：

 

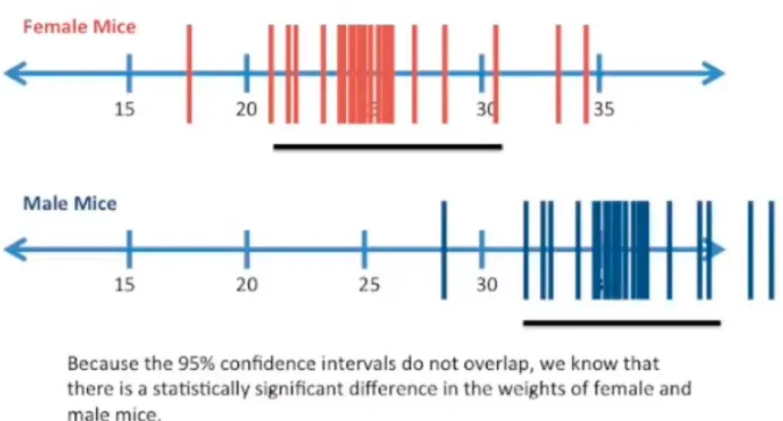
 （图来自：https://www.zhihu.com/question/24801731）

 

PS: 置信区间主要是对总体期望的一个估计，用这个区间来评估总体的样本分布是不适合的。比如一个基于某种工艺的工业产品，我们需要她的总体期望为100，我们试生产并采样后得到的置信区间如果为[110，120]，我们可以认为这个总体分布是没有达到预期的，但是如果我们采样后的置信区间为[90，110]，那么实际上我们也不能确认该工艺是否达到了我们的要求，这就需要使用其他的方式继续评估了。所以说，置信区间的使用并没有那么万能，在使用时需要注意防止误用。

 

 

----------------------------------------

 

 

posted on 2022-12-04 23:46  Angry_Panda  阅读(397)  评论(0)  编辑  收藏  举报

导航