算法之数值的整数次方

要求：实现特定库函数pow.

解决思路：首先常规的解法大家肯定都会，这里主要是一种高效而且很全面的方法。我们要考虑如果输入的指数小于1，也就是零和负数的时候，怎么办呢?

这样办，可以先对指数求绝对值，然后算出次方的结果后，再取倒数。那么，问题来了，底数是0的时候，0没有倒数啊，假如你对0求了倒数，那岂不是让程序出错。
为了不使程序出错，这里做一下特殊处理。当底数为0而且指数是负数的时候，我们设立一个布尔型的全局变量，出错时，全局变量为true，返回值为0；

那么不出错的时候，全局变量也就是false了。

代码中用到的公式说明：如果输入的指数是exponent为32，则在函数powerwithunsignedexponent的循环中需要做31次乘法。但是我们其实可以不用这么多次的。
如何做？平方的思想！如果你要求2的8次方，那么在算到2的4次方的时候，把2的4次方平方一下，就得到2的8次方。

同理，若求2的16次方，直接把2的8次方平方一下，那么，是不是就少了很多次的乘法步骤呢。

必然，这就是平方的强大之处。所以有如下的公式，我们直接用就好了。

求a的n次方：

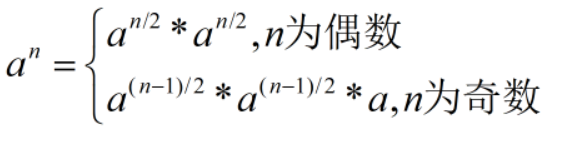
核心代码：
'''

bool g_invalidinput=false;
double  power(double base,int exponent)
{
 g_invalidinput=false;//全局变量
 if((equal(base,0,0)&(exponnent<0)
{
   g_invalidinput=true;
   return 0.0;
 }
 unsigned int absexponent=(unsigned int)(exponent);//指数的绝对值为无符号型整数
 if(exponent<0)
     absexponent=(unsigned int)(-exponent);
 double result=powerwithunsignedexponent(base,absexponent)
 if(exponent<0)
      result=1.0/result;
 return result;
 double powerwithunsignedexponent(int base,unsigned int exponent)
{
  if(exponent==0)

     return 1；
  if(exponent==1)
      
    return base;
  double result = powerwithunsignedexponent(base, exponent >> 1);//递归
  //利用右移来代替除法，提高效率
  result*=result;//利用公式
  if(exponent&0x1==1)//判断奇偶性，如果为奇，那么还要乘以base.
     return result*base;
  return result;//若为偶，平方后直接输出即可

整体代码（包含测试）：
'''

#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<iostream>
using namespace std;
double powerwithunsignedexponent(double base, unsigned int exponent);
bool g_invalidinput = false;//有效位设为false。
bool equal(int num1, int num2)//判断两数是否相同
{
if ((num1 - num2 > -0.0000001) && (num1 - num2 < 0.0000001))
	return true;
else
	return false;
}
 double power(double base, int exponent)//考虑到特殊情况
 {
g_invalidinput = false;
if  (equal(base,0.0) && exponent < 0)//底数为0，指数为负数的情况
{
	g_invalidinput = true;//出错时为true
	return 0.0;//返回0.0
}
unsigned int absexponent = (unsigned int)(exponent);
if (exponent < 0)//当指数为负数的时候，先取绝对值，然后再求倒数
{
	absexponent = (unsigned int)(-exponent);
}
double result = powerwithunsignedexponent(base, absexponent);
if (exponent < 0)

	result = 1.0 / result;//对结果取倒数
return result;

   }
  double powerwithunsignedexponent(double base, unsigned int exponent)
  {//这是求幂的运算
    if (exponent == 0)
       return 1;
	if (exponent == 1)
		return base;
	
	double result = powerwithunsignedexponent(base, exponent >> 1);
	//利用右移来代替除法，提高效率
	result *= result;//利用公式
	if (exponent & 0x1 == 1)//判断奇偶性，如果为奇，那么还要乘以base.
		result *= base;
	return result;//若为偶，平方后直接输出即可
   }
 void test(const char* testname, double base, int exponent, double expectedresult, bool expectedflag)
{
double result = power(base, exponent);
if (equal(result, expectedresult) && g_invalidinput == expectedflag)
	std::cout << testname << " passed" << std::endl;
else
	std::cout << testname << "failed" << std::endl;
}
int main(int argc, char* argv[])
{
test("test1", 3, 2, 9,false );
test("test2", -2, 3, -8, false);
test("test3", 0, -1, 0, true);//底数为0，指数为负数的时候，特殊处理
}