LeetCode——删除回文子数组
Q:给你一个整数数组 arr,每一次操作你都可以选择并删除它的一个 回文 子数组 arr[i], arr[i+1], ..., arr[j]( i <= j)。
注意,每当你删除掉一个子数组,右侧元素都会自行向前移动填补空位。
请你计算并返回从数组中删除所有数字所需的最少操作次数。
示例 1:
输入:arr = [1,2]
输出:2
示例 2:
输入:arr = [1,3,4,1,5]
输出:3
解释:先删除 [4],然后删除 [1,3,1],最后再删除 [5]。
A:
经典的区间dp,我们令f(i,j)f(i,j)代表删除区间[i,j][i,j]的最小值(即最小删除次数),那么可得以下递推公式:
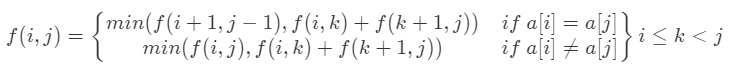
分析一下,这里根据a[i]是否等于a[j],分两种情况。因为当a[i] = a[j]的时候,有可能产生最小删除次数的方案是a[i]和a[j]等到最后一起被删。
public int minimumMoves(int[] arr) {
int n = arr.length;
int[][] dp = new int[n][n];
// 单个字符也是回文串,删除单个字符的最小删除次数就是1
for (int i = 0; i < n; i++) {
dp[i][i] = 1;
}
for (int j = 1; j < n; j++) {
for (int i = j - 1; i >= 0; i--) {
if (i == j - 1) {
// 就两个元素
dp[i][j] = arr[i] == arr[j] ? 1 : 2;
continue;
}
// 下面至少三个元素
int min = Integer.MAX_VALUE;
if (arr[i] == arr[j]) {
// 头尾相等,最小值有可能是出现在这对头尾最后被删的结果
min = dp[i + 1][j - 1];
}
for (int k = i; k < j; k++) {
min = Math.min(min, dp[i][k] + dp[k + 1][j]);
}
dp[i][j] = min;
}
}
return dp[0][n - 1];
}



