%zsy %lqs 随感

今天是cj的大毒瘤zsy(对对，您说的都对，题目不难的啦，是我太菜啦)出题。

我校选手lqs仍然坚持高水平的发挥，wzy神犇却不在状态。

面对T1sb题(其实干了2h)和T3的原题(我&lqs&wzy当初一起花了1.5h切了的not that hard problem)，果断3h写完230分开始颓b站(大力哥出狱啦，鬼畜真心爽啊)。

随后当了一把星际选手，眼瞎般的交错了代码。呜呜呜。。。

省选前考试的状态一点也没有，感觉只会写水题(还写不对)，被wzy&lqs&nickluo&...爆踩。

我不想退役啊。。。看来要更认真才行了。

不然以后就不一定能踩lqs了，那多不爽啊。。。

左：lqs，右：xy

20190311

 

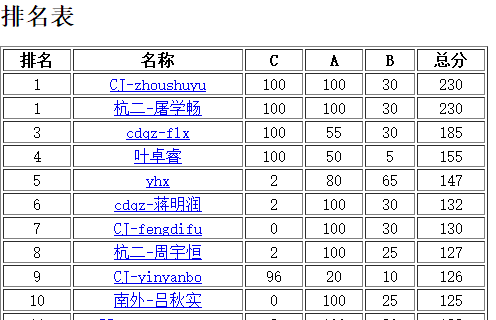
20190312

 

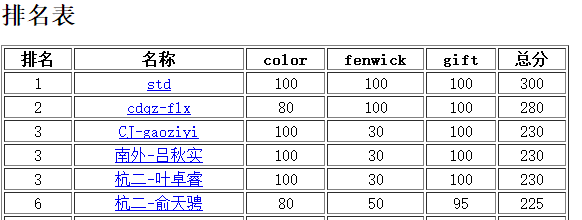
主要记一下T1吧，$f_{i,j}=f_{i,j}+\sum_{k=0}^{j-1} f_{i-1,k}*(k+1)$

考虑$f_{i,j}-f_{i,j-1}=f_{i-1,j}+(j-1)*f_{i-1,j-1}$，即$f_{i,j}=f_{i-1,j}+f_{i,j-1}+(j-1)*f_{i-1,j-1}$

不难认为这是一个平面数路径问题，斜边边权为j，开始计数

不难发现走的斜边个数相同的情况对应的NE lattice path的计数系数是一样的

于是分治fft一下，利用第一类斯特林数的O(nlogn)做法，我们也可以做到O(nlogn)。

#include<bits/stdc++.h>
using namespace std;
const int N=4000005,mod=998244353;
int n,m,ans,a[N],b[N],S[N],r[N],fac[N],ifac[N];
inline int pw(int a,int b){int r=1;for(;b;b>>=1,a=1ll*a*a%mod)if(b&1)r=1ll*r*a%mod;return r;}
inline int C(int a,int b){return 1ll*fac[a]*ifac[b]%mod*ifac[a-b]%mod;}
inline void ntt(int n,int *a,int f)
{
    int l=0;while((1<<l)<n)l++;
    for(int i=1;i<n;i++)r[i]=r[i>>1]>>1|(i&1)<<(l-1);
    for(int i=0;i<n;i++)if(i<r[i])swap(a[i],a[r[i]]); 
    for(int i=1;i<n;i<<=1)
    {
        int wn=pw(3,(mod-1)/(i<<1));
        if(f==-1)wn=pw(wn,mod-2);
        for(int j=0;j<n;j+=(i<<1))for(int k=0,w=1;k<i;k++,w=1ll*w*wn%mod){int u=a[j+k],v=1ll*a[j+k+i]*w%mod;a[j+k]=(u+v)%mod;a[j+k+i]=(u+mod-v)%mod;}
    }
    if(f==-1)for(int i=0,iv=pw(n,mod-2);i<n;i++)a[i]=1ll*a[i]*iv%mod;
}
void sol(int n)
{
    if(n==1){S[0]=0;S[1]=1;return;}
    if(n&1){sol(n-1);for(int i=n;i;i--)S[i]=(S[i-1]+1ll*(n-1)*S[i])%mod;return;}
    sol(n>>1);n>>=1;
    for(int i=0,p=1;i<=n;i++)a[i]=1ll*p*ifac[i]%mod,p=1ll*p*n%mod;
    for(int i=0;i<=n;i++)b[i]=1ll*fac[n-i]*S[n-i]%mod;
    n++;int nn=1;while(nn<(n<<1))nn<<=1;
    for(int i=n;i<nn;i++)a[i]=b[i]=0;
    ntt(nn,a,1);ntt(nn,b,1);
    for(int i=0;i<nn;i++)a[i]=1ll*a[i]*b[i]%mod;
    ntt(nn,a,-1);reverse(a,a+n);
    for(int i=0;i<n;i++)a[i]=1ll*a[i]*ifac[i]%mod;
    for(int i=n;i<nn;i++)S[i]=a[i]=0;
    ntt(nn,S,1);ntt(nn,a,1);
    for(int i=0;i<nn;i++)S[i]=1ll*S[i]*a[i]%mod;
    ntt(nn,S,-1);
}
int main()
{
    freopen("color.in","r",stdin);
    freopen("color.out","w",stdout);
    scanf("%d%d",&n,&m);n--;m--;
    if(!n||!m){puts("1");return 0;}
    for(int i=fac[0]=1;i<=n+m;i++)fac[i]=1ll*fac[i-1]*i%mod;
    ifac[n+m]=pw(fac[n+m],mod-2);
    for(int i=n+m;i;i--)ifac[i-1]=1ll*ifac[i]*i%mod;
    n++;sol(n);n--;
    for(int i=0;i<=n;i++)ans=(ans+1ll*C(n+m-i,n)*S[n+1-i])%mod;
    printf("%d\n",ans);
    return 0;
}

再次%zsy，%lqs。奶一口zsy和lqs省队稳啦。 

(决定啦，像lqs这样又假又强的人后天我xy一定要认真地踩他一次，23333，xy加油啦。)

Upd1：zsy果然稳 orz HN队长！~

Upd2：lqs tql, 所以踩lqs的计划一直咕咕咕~

Upd3：在JSOI2019R2中终于比lqs高一点了(开心！)，所以lqs似乎被我送出队了。。。

（不过一共4个名额，我校内rk3应该不怪我吧QwQ）~

Upd4：据说。。。lqs应该可能有希望进队？如果学长们进国家队的话。。。 

Upd5：lqs进队了，因为FizzyDavid进国家队了。。。