线段树是一种比较复杂的数据结构,可用来对一个数组进行维护(查询,求和,计算等)操作。
1. 线段树的特点
线段树是一种二叉树,它的每个节点,存储的是原始数组内一段区间内的某些信息,这些信息满足(幺)半群的性质。每个节点的左右孩子存储的区间为父节点区间的一半。设父节点是存储[L,R]区间,L,R为左右端点,M = (L+R)/2为区间的中点,原区间[L,R]可以被分为分解成[L,M]和[M+1,R] ,左孩子存储[L,M],右孩子存储[M+1,R]。线段树就这不断将一个区间一分为二,直到区间内只剩下一个元素。
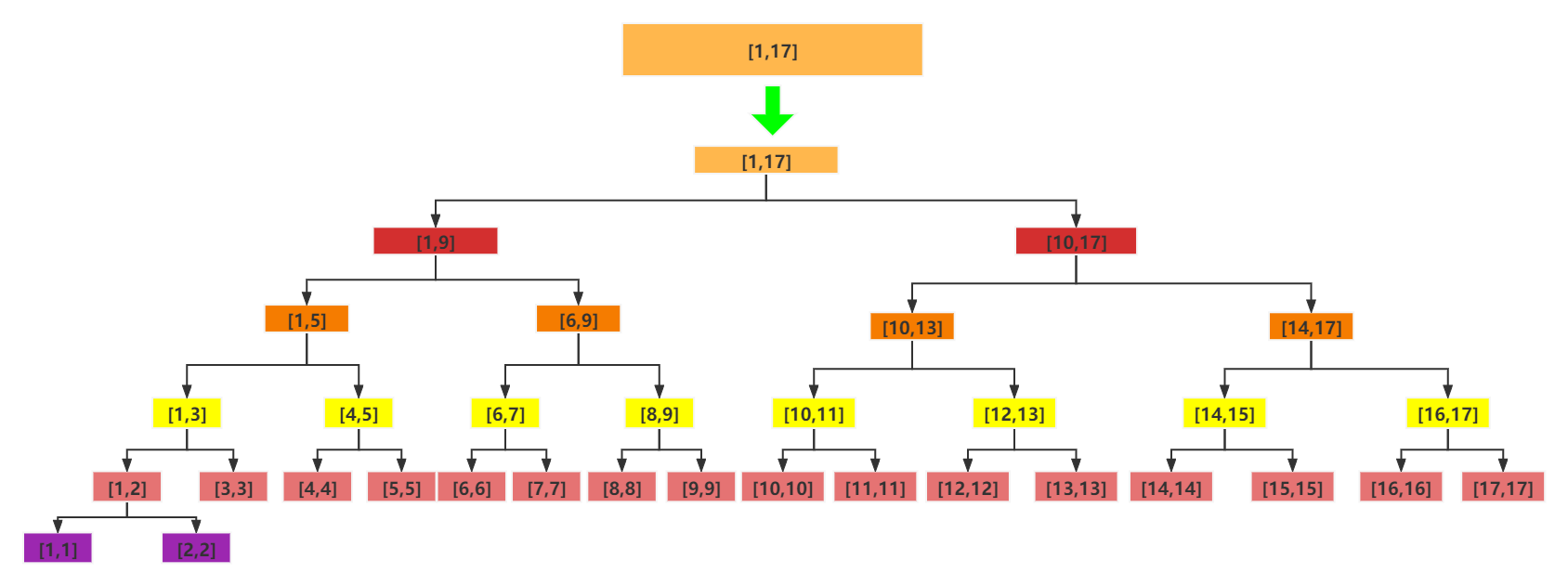
从上面的可以看出,线段树的思想实际上是将一个数组,或者说一段区间中的信息分散存储在二叉树的不同层当中,越浅的层存的信息越总体,越深的层存的信息越详细。同一层保存的区间不重合,这样在求某段区间信息的时候,就可以通过线段树找到对应的区间,然后再合并这些区间,得到最终的解。例如,如果要求区间[5,11],就可以在线段树中查找对应的区间(具体的查找方法后文有介绍)。

从分解的过程中可以看出,线段树近似于完全二叉树,实际上可证明线段树是平衡二叉树(证明略),所以查找的时间复杂度为$O(logN)$。
2.如何表示一颗线段树?
2.1 建树表示
第一种存储线段树的方式就是使用链表,这种方式比较传统。
2.2 使用数组模拟
另一种表示线段树的方法是使用数组模拟。因为线段树是平衡二叉树,所以只要线段树总的节点数为原数组元素个数的两倍左右。因此只要开辟4倍于原数组的存储空间,就可以保证线段树的存储。
使用数组模拟的方式比较简单,因此在下面对线段树功能的讲解中,采用这种方式。
3. 线段树常见的操作和功能?
3.1 建树
3.2 点更新
3.3 区间查询
3.4 区间修改
以上就是线段树的入门内容,介绍了线段树的基本特点和操作。但是要想彻底搞清楚线段树还不仅于此。比如,我们要能够判断,哪些问题可以通过线段树解决,要学会将遇上的问题转化为线段树解决,这些都需要不断练习。另外在程序设计竞赛中,线段树还有其他一些更加巧妙的操作,有兴趣的朋友可以找资料进一步学习。如果以后我有时间,也可能会继续更新。



