二叉搜索树介绍
二叉搜索树(Binary Search Tree,简称BST),又叫二叉排序树,二叉查找树,是一种特殊的树型结构,它有如下特点。
任一节点的左(右)子树中,所有节点(若存在)均不大于(不小于)r。我们把这种特点叫做顺序性。

二叉搜索树的数据结构:
1 struct node 2 { 3 int data; 4 node*lchild,*rchild,*parent; 5 };
常用操作介绍
1. 查找
查找是二叉搜索树最主要的功能,二叉搜索树的顺序性也利于查找的实现。和二分法类似,可以采用分治算法的思想进行,逐步缩小查找范围,直到发现目标或搜索范围为空。用一个流程图来表示就是下面这样:
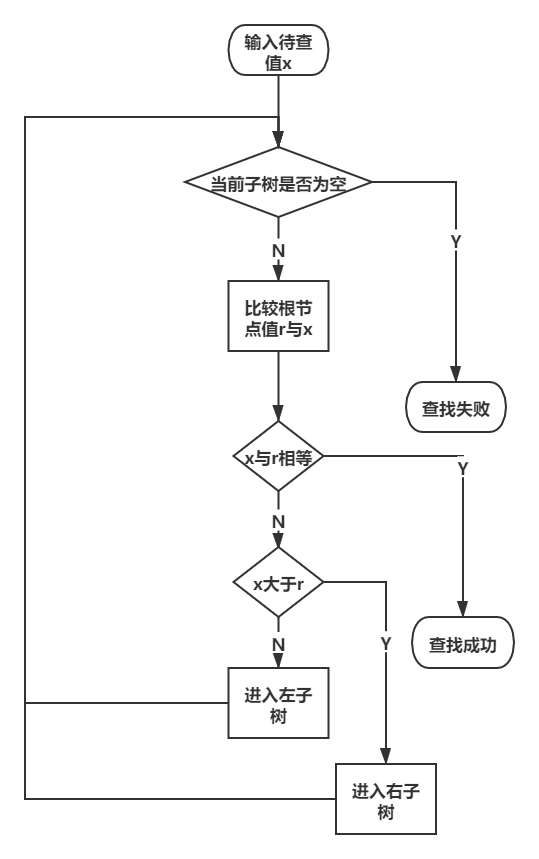
查找代码实现:
1 node*findNode(int data,node*Node) 2 { 3 if(!Node) 4 return nullptr; 5 else 6 { 7 if(Node->data==data) 8 return Node; 9 return Node->data>data?findNode(data,Node->lchild):findNode(data,Node->rchild); 10 } 11 }
2. 插入
二叉搜索树的顺序性便于查找,但是却给搜索树的维护和更新带来了一点困难,在插入和删除节点的时候,必须要保持二叉搜索树作为数据结构的完整性和一致性。相比删除操作,插入操作更容易理解一点。假设有一个序列为{23,3,24,54,12},我们拿这个这个序列建一个二叉查找树,模拟一下插入操作。
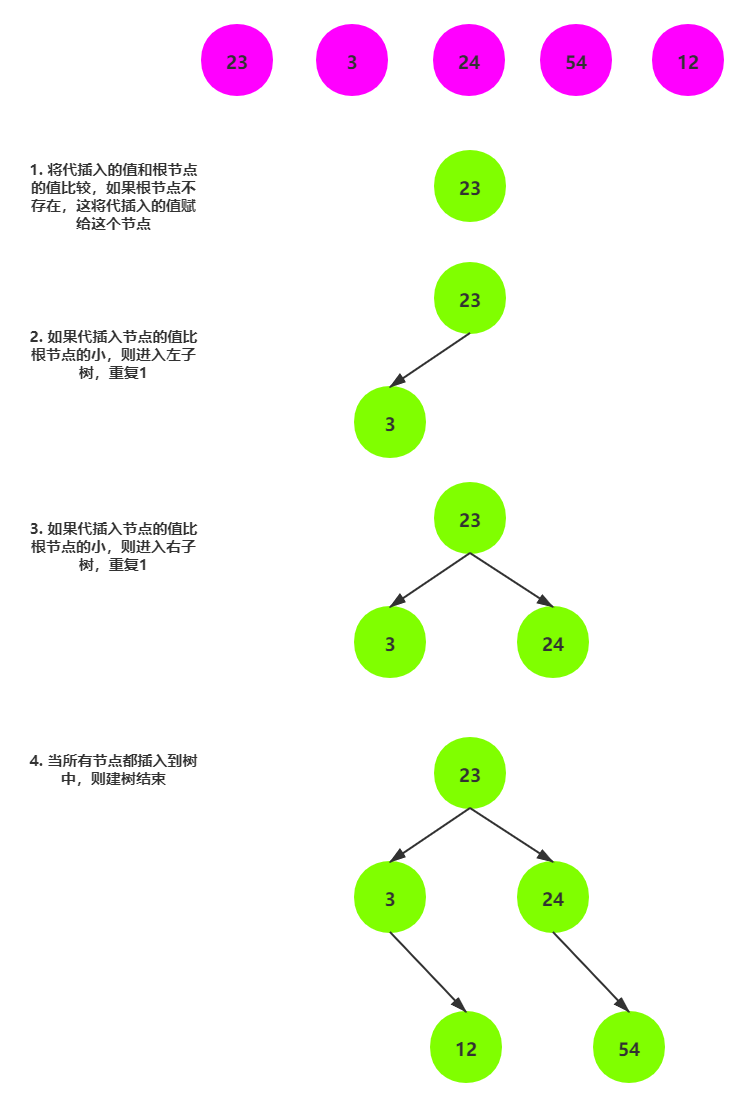
插入代码实现
1 void insertNode(int data,node*&BSTree,node*parent) 2 { 3 if(!BSTree) 4 { 5 BSTree = new node; 6 BSTree->data = data; 7 BSTree->lchild = BSTree->rchild = nullptr; 8 BSTree->parent = parent; 9 return; 10 } 11 BSTree->data>data?insertNode(data,BSTree->lchild,BSTree):insertNode(data,BSTree->rchild,BSTree); 12 return; 13 }
3. 删除
相比于插入算法,二叉搜索树的删除算法要更复杂一点,要分为三种情况处理:
1. 删除的节点是叶子节点,这种情况很好处理,只要把该节点删除就好了


2. 删除的节点有一颗左子树或者右子树,那么用这棵子树的根节点替换被删除的节点
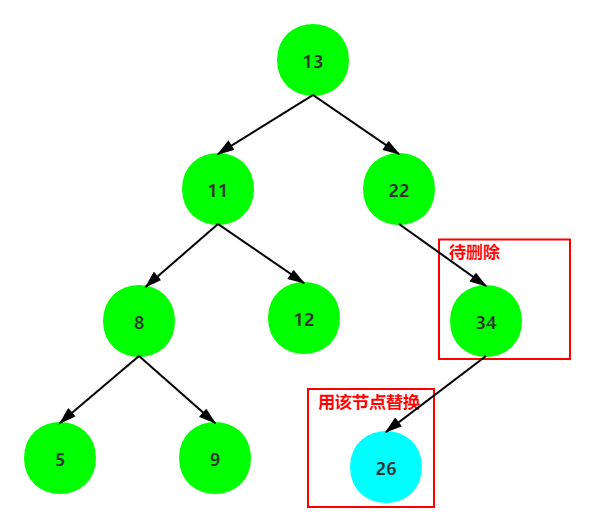
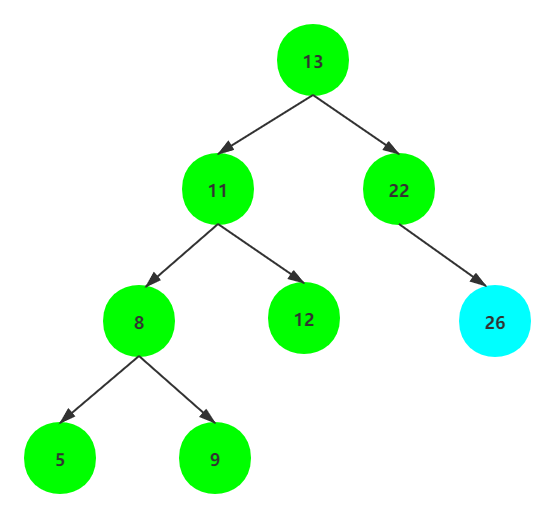
3. 最麻烦的情况就是被删除的节点同时拥有左子树和右子树
这个时候我们需要寻找的被删除节点的直接后继节点,也就是在该节点右子树最小的那个节点。注意,这个时候该节点不可能有左子树,否则它不会是最小的节点,那么,就可以分为两种情况:
1. 直接后继节点的父亲节点是待删除节点,那用这个后继节点替换待删除节点,如果它有右子树,则右子树依然属于该节点。
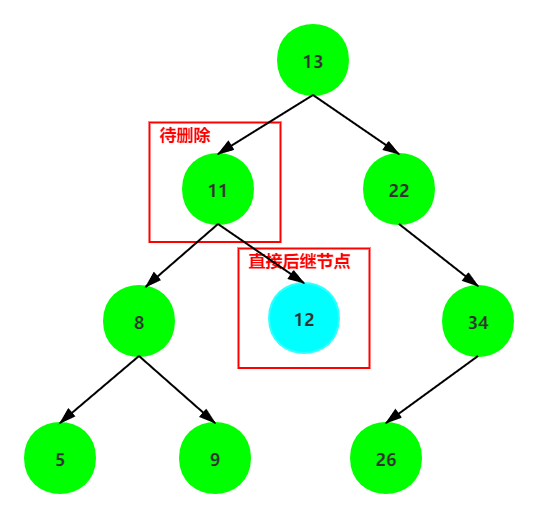



2. 直接后继节点是的父亲节点是不待删除节点自身,则除了用这个后继节点替换待删除节点以外,如果它有右子树,那还要它的右子树交给它的父亲节点做左子树。
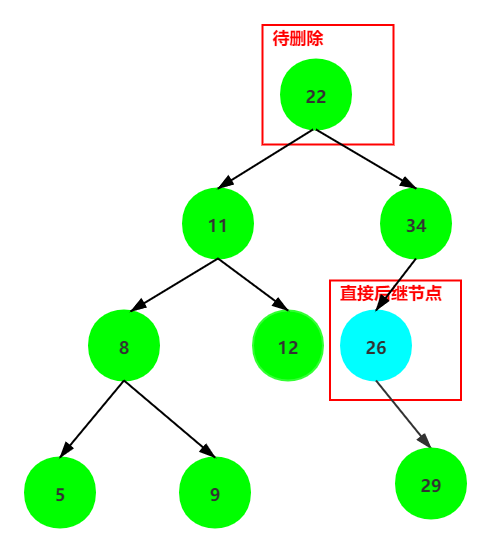
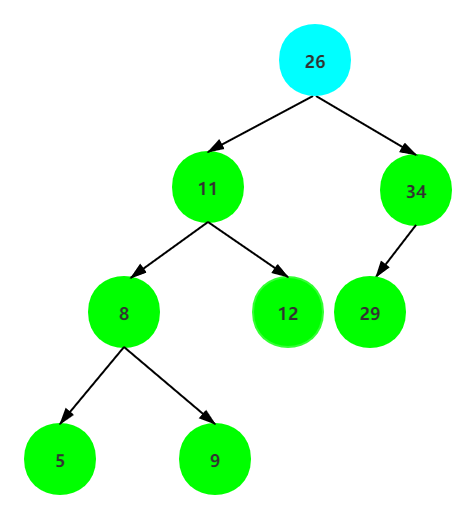
删除代码实现:
1 node*findNextNode(node*Node) 2 { 3 if(!Node->lchild) 4 return Node; 5 else 6 return findNextNode(Node->lchild); 7 } 8 void removeNode(int data,node*BSTree) 9 { 10 node*delNode = findNode(data,BSTree); 11 if(!delNode->lchild&&!delNode->rchild) // 叶子节点 12 { 13 if(delNode->parent) //假设双亲节点存在 14 { 15 node*tmp = delNode->parent; 16 if(tmp->lchild==delNode) tmp->lchild = nullptr; 17 if(tmp->rchild==delNode) tmp->rchild = nullptr; 18 } 19 delete delNode; 20 } 21 else if((!delNode->lchild&&delNode->rchild)||(!delNode->rchild&&delNode->lchild)) //有一棵左子树或者右子树 22 { 23 node*NextNode = delNode->lchild?delNode->lchild:delNode->rchild; 24 if(delNode->parent) 25 { 26 node*tmp = delNode->parent; 27 NextNode->parent = tmp; 28 tmp->lchild==delNode?tmp->lchild=NextNode:tmp->rchild=NextNode; 29 } 30 else 31 NextNode->parent = nullptr; 32 delete delNode; 33 } 34 else //最复杂的情况 35 { 36 node*NextNode = findNextNode(delNode); //找到后继节点 37 node*NextNodeParent = NextNode->parent; // 找到后继节点的父亲节点 38 if(NextNodeParent==delNode) 39 { 40 if(delNode->parent) 41 { 42 node*tmp = delNode->parent; 43 NextNode->parent=tmp; 44 tmp->lchild==delNode?tmp->lchild=NextNode:tmp->rchild = NextNode; 45 delNode->lchild->parent = NextNode; 46 NextNode->lchild = delNode->lchild; 47 } 48 else 49 { 50 delNode->lchild->parent = NextNode; 51 NextNode->lchild = delNode->lchild; 52 } 53 } 54 else 55 { 56 swap(NextNode->data,delNode->data); 57 if(NextNode->rchild) 58 { 59 NextNodeParent->lchild = NextNode->rchild; 60 NextNode->rchild->parent = NextNode; 61 } 62 } 63 delete delNode; 64 } 65 return; 66 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号