上一篇博客介绍了串匹配问题的定义和蛮力(Brute Force)算法的实现,并且通过分析得出,在最好的情况下,执行一次蛮力算法的时间,是文本串T长度n和模式串P长度m的乘积,即它的最坏时间复杂度为O(nm)。不难想象,当文本串很长时,运行蛮力算法的时间成本相当高。那么,有没有办法能优化串匹配算法,来降低它的时间复杂度呢?今天介绍的KMP算法就是流传最广的串匹配优化算法。
KMP算法
KMP 算法是 D.E.Knuth、J,H,Morris 和 V.R.Pratt 三位大牛共同提出的,因此称之为 Knuth-Morria-Pratt 算法,简称为 KMP 算法。KMP算法是针对蛮力算法的一种改进。要想弄懂KMP算法,我们就要弄清楚,蛮力算法有何不足之处。首先我们先设想一种蛮力算的最坏情况,然后进行分析。不难发现,蛮力算法最坏的情况,就是每一轮匹配到最后一个字母才失配,例如下图这种情况。

使用蛮力算法,会逐个比较文本串和模式串,如果匹配,则继续比较。
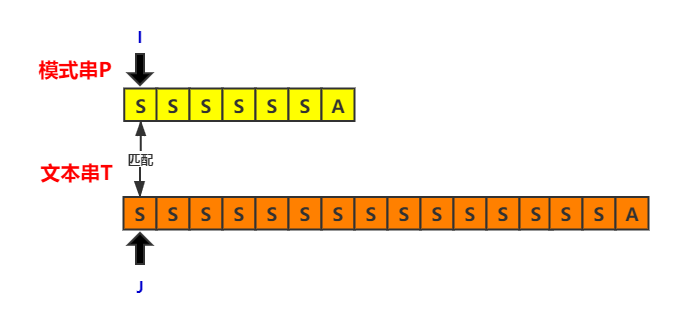
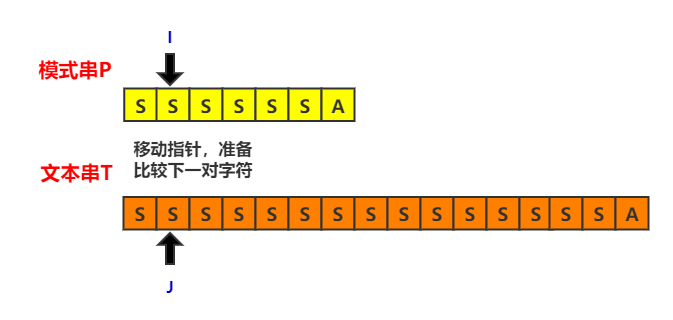
在前六次比较中,两者都是匹配的$(T[j] = P[i])$,直到最后一次比较才失配,这个时候指向文本串的指针i会回退,重新开始下一轮比较。
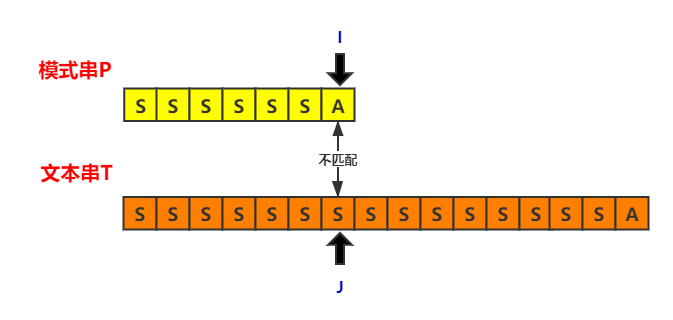
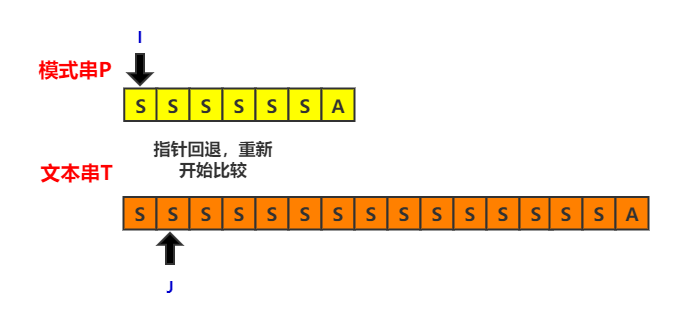
从中我们可以发现,蛮力算法的时间主要浪费在指针的回退上。如图可见,在第一次匹配的时候,指向文本串的指针j就已经移动到了第七位,但一旦发生失配,它就会必须移动到第二位,重新开始另一次匹配的过程。因此,想要降低串匹配的时间复杂度,我们就要尽量减少j指针的回退,甚至让它不要回退。
文本串指针回退以后的情况分析
再分析文本串指针的回退情况之前,我们先补充几个关于串的知识
1. 子串
字符串中任一连续的片段,称作其子串(substring)。具体地,对于任意的$0 \leqslant i \leqslant i +k < n$,由字符串S中起始于位置i的连续k个字符组成的子串记作:
$$
"a_{i}a_{i+1}...a_{i+k-1}"=S\left[ i,i+k \right]
$$
2. 前缀和后缀
起始于位置$0$、长度为$k$的子串称为前缀(prefix),而终止于位置$n - 1$、长度为$k$的子串称为后缀(suffix),分别记作:
$$
prefix\left( S,k \right) =S\text{[0,}k\text{)}\\
suffix\left( S,k \right) =S\text{[}n-k,n\text{)}
$$
然后我们分析文本串的指针回退以后的情况,首先,选择新的子串t
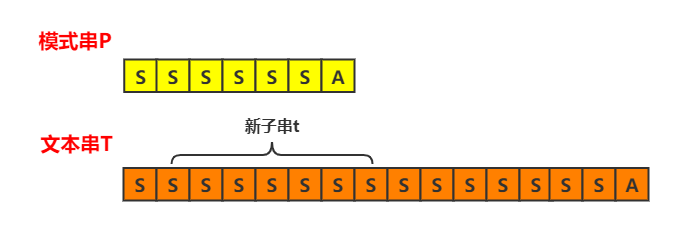
不难发现,新选取子串的长度为5的前缀,在前一轮匹配中,和模式串是匹配成功的,即$t[0,5) = P[1,6)$
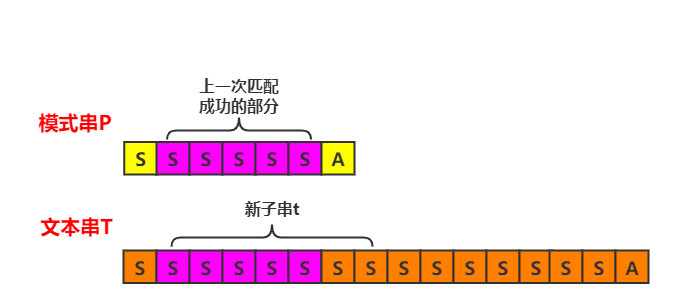
这个前缀在这一轮匹配中,会和模式串的前缀,即$P[0,5)$进行匹配
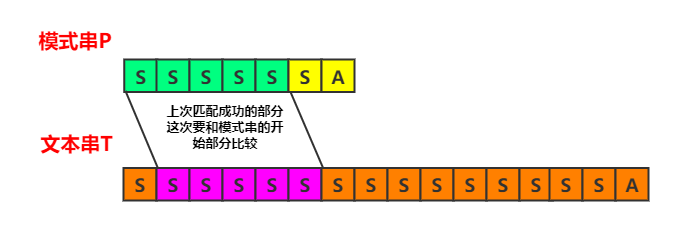
因为模式串P的前六个字符都是S,所以有:
$$ t[0,5) = P[0,5) = P[1,6) $$
因此子串t的这部分前缀没有再次匹配的必要,可以直接从第六个字符进行比较,而第六个字符就是上一次匹配失配的位置,我们只需要将模式串的指针指向第六个字符,就可以开始这一轮比较。
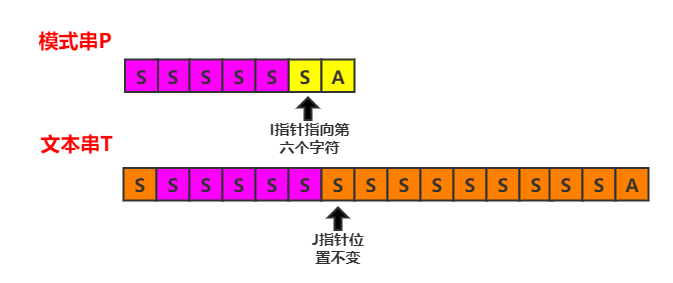
从上面这个例子我们可以看出,文本串指针的位置其实和上一轮匹配过程中,匹配成功的子串的前后缀有关。
假设在上一轮匹配中,$T[j] \ne P[i]$ ,在此之前,有$P[0,i) = T[j-i,j)$

那么在下一次匹配中,需要用到子串T[j-i,j]长度为k的后缀T[j-k,j)去和模式串P长度为k的前缀P[0,k)匹配。
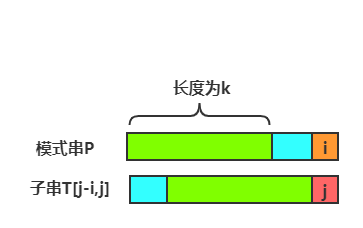
如果能匹配上,则有
$$ P[0,k) = T[j-k,j) $$
又因为P[0,i) = T[j-i,j),必有
$$ T[j-k,j) = P[i-k,i) $$
所以
$$ P[0,k) = T[j-k,j) = P[i-k,i) $$
这意味着,匹配成功的必要条件是模式串在i之前的子串P[0,i)一定要有相等的前缀和后缀。否则的话匹配一定不成功。这些子串的长度k,组成集合N
$$
N = \{k | P[0,k) = P[i-k,i)\}
$$
文本串指针真的需要回退吗?
进一步分析了文本串指针回退后的操作,结合模式串的前缀和后缀,可以发现,其实文本串的指针根本没有回退的必要,因为回退无非有两种情况
1. 前面局部匹配的子串中,不存在相等的前缀和后缀。按照上面的流程可以发现,如果不存在这样的前缀和后缀,匹配不可能成功。
2. 前面局部匹配的子串中,存在匹配的前缀和后缀。这种情况说明新选定的子串和模式串前面是匹配上的,那这部分就不需要重新比较了。
因此,下一次比较从匹配的前缀的后一个字符,即P[k]处开始

更一般的情况
按照上面的流程,我们再来分析一个更一般的情况。模式串为ABCAABC,文本串为ABCAEABCD。
模式串的Next数组为
如图,第一次匹配中,文本串和模式串前四个字符匹配,在第五个字符处失配
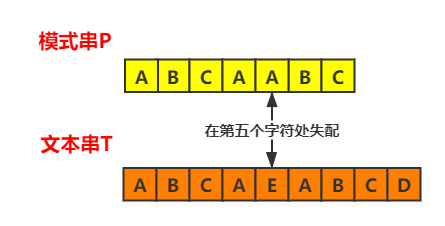
匹配成功的子串为ABCA,ABCA的真前缀为{A,AB,ABC},真后缀为{A,CA,BCA}。
ABCA的真前缀和真后缀中只有一对相等,长度为1,所以要从模式串的第二个字符处比较
next数组
在确定了文本串的指针不用回退以后,那需要做的,就是判断模式串指针的位置。从上面的分析可以看出,P长度为k的前缀P[0,k)不需要比较,这一轮的比较从P[k]开始,为了不移除任何的可能,k取N中的最大值。即 k = max(N)。我们将P在不同的位置失配得到的k用一个数组记录下来,这个数据就是KMP算法中最重要的next数组。next数组可以用来确定模式串指针的位置。
构建next数组的代码如下
1 int*buildnext(char*P) 2 { 3 int i=0; 4 size_t m = strlen(P); 5 int*next = new int[m]; 6 next[0] = -1; 7 int t = next[0]; 8 while(j<m-1) 9 { 10 if(t<0||P[j]==P[t]) 11 { 12 j++,t++; 13 N[j] = t; 14 } 15 else 16 t = N[t]; 17 } 18 return next 19 }
得到next数组之后,我们可以得到最终的代码,它只要在BF算法的基础上结合next数组,就可以获得。
1 int KMP(char*T,char*P) 2 { 3 int*next = buildNext(P); 4 int i=0,j=0; 5 int m = strlen(P),n = strlen(T); 6 while(j<m&&i<n) 7 { 8 if(0>j||T[i]==P[j]) 9 { 10 i++; 11 j++; 12 } 13 else 14 j = next[j]; 15 } 16 delete [] next; 17 return i-j; 18 }
时间复杂度
因为文本串的指针不需要回退,所以KMP算法最多只需要执行n+m次,它的时间复杂度为O(n+m)



