opencv实战——PCA算法的应用

摘要

上一篇详细叙述了PCA的数学原理opencv——PCA（主要成分分析）数学原理推导 - 唯有自己强大 - 博客园 (cnblogs.com)

本篇就来说一说PCA在opencv项目中的应用：

获取物体主要方向（形心）
对数据集降维处理

1️⃣什么是PCA?

PCA的主要思想是寻找到数据的主轴方向，由主轴构成一个新的坐标系，这里的维数可以比原维数低，然后数据由原坐标系向新的坐标系投影，这个投影的过程就可以是降维的过程。

PCA 是一种非监督的算法, 能找到很好地代表所有样本的方向, 但这个方向对于分类未必是最有利的，通过下图可以更直观地了解PCA的作用：

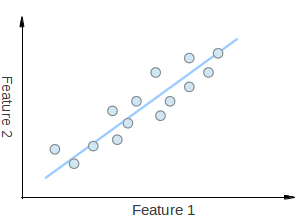
假设有上图所示的一组2维点，其中每个维度与您感兴趣的功能相对应。有些人可能会争辩说，这些点是随机的，但有一个线性模式（由蓝线表示），这是很难忽视的。可以将一组点近似于单行，即将点的尺寸从2维降低到1维。维度降低是人工智能和数据挖掘的关键技术。你还可以看到，这些点沿蓝线变化最大，比沿Feature1 轴或Feature2轴变化的要多。这意味着，如果你知道沿蓝线的点的位置，则你掌握的关于该点的信息比你只知道它在Feature1 轴或Feature2轴上的位置要多。

因此，PCA 是一种数学工具，它使我们能够找到数据变化最大的方向。事实上，在图表中的一组点上运行 PCA 的结果由 2 个称为eigenvector（特征向量） 组成，这些载体是数据集的主要组件。

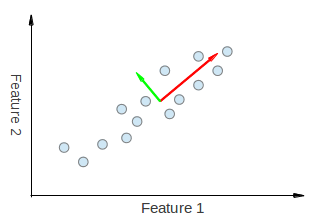
每个 eigenvector（特征向量）的大小被编码在相应的eigenvalue（特征值）中，并指示数据沿主要组件变化的程度。（通过这个特性可以获取物体(轮廓）的主要方向）

eigenvectors（特征向量）的开头是数据集中所有点的中心。（通过这个特性可以获取物体（轮廓）的形心）

2️⃣opencv中的PCA类

PCA类的成员函数包括构造函数、运算符重载（）、project、backProject这几个函数，还包括成员变量eigenvectors、eigenvalues、mean。使用也很方便。比如我要计算一组向量的PCA，我们只需要定义个PCA实例，获得主成分，调用project测试新样本，也可以再调用backProject重建原始向量，是project的一个逆运算。

🎈opencv中PCA类的主要函数有：

构造函数PCA

PCA::PCA(InputArray data, InputArray mean, int flags, int maxComponents=0)
data           //输入数据（可以是轮廓点集）
mean           //数据零均值，为空（Mat（））时自动计算
flag           //表示数据提供的方式（0表示按行输入，1表示按列输入）
maxComponents  //保留多少特征值（默认全保留）

原图像，投影到新的空间

Mat PCA::project(InputArray vec) const

进行project之后的数据，反映摄到原始图像

Mat PCA::backProject(InputArray vec) const

变量值有：mean--------原始数据的均值

eigenvalues--------协方差矩阵的特征值

eigenvectors--------特征向量

3️⃣PCA获取物体主要方向（形心）

opencv实现：

int main(int argc, char** argv)
{    
    double getOrientation(vector<Point> &pts, Mat &img);
    Mat src = imread("D:/opencv练习图片/PCA分析1.png");
    imshow("输入图像", src);
    Mat gray,binary;
    cvtColor(src, gray, COLOR_BGR2GRAY);
    //阈值处理
    threshold(gray, binary, 150, 255, THRESH_BINARY);
    imshow("二值化", binary);
    //寻找轮廓
    vector<vector<Point> > contours;
    vector<Vec4i> hierarchy;
    findContours(binary, contours, hierarchy, RETR_LIST, CHAIN_APPROX_NONE);
    //轮廓分析，找到工件
    for (size_t i = 0; i < contours.size(); ++i)
    {
        //计算轮廓大小
        double area = contourArea(contours[i]);
        //去除过小或者过大的轮廓区域（科学计数法表示le2表示1X10的2次方）
        if (area < 1e2 || 1e4< area) continue;
        //绘制轮廓
        drawContours(src, contours, i, Scalar(0, 0, 255), 2, 8, hierarchy, 0);
        //寻找每一个轮廓的方向
    double angle=    getOrientation(contours[i], src);
    cout << angle << endl;
    }
    
    imshow("结果", src);    
    waitKey(0);
    return 0;
}
//获得构建的主要方向
double getOrientation(vector<Point> &pts, Mat &img)
{
    //构建pca数据。这里做的是将轮廓点的x和y作为两个维压到data_pts中去。
    Mat data_pts = Mat(pts.size(), 2, CV_64FC1);//使用mat来保存数据，也是为了后面pca处理需要
    for (int i = 0; i < data_pts.rows; ++i)
    {
        data_pts.at<double>(i, 0) = pts[i].x;
        data_pts.at<double>(i, 1) = pts[i].y;
    }
    //执行PCA分析
    PCA pca_analysis(data_pts, Mat(), 0);
    //获得最主要分量（均值），在本例中，对应的就是轮廓中点，也是图像中点
    Point pos = Point(pca_analysis.mean.at<double>(0, 0), pca_analysis.mean.at<double>(0, 1));
    //存储特征向量和特征值
    vector<Point2d> eigen_vecs(2);
    vector<double> eigen_val(2);
    for (int i = 0; i < 2; ++i)
    {
        eigen_vecs[i] = Point2d(pca_analysis.eigenvectors.at<double>(i, 0), pca_analysis.eigenvectors.at<double>(i, 1));
        eigen_val[i] = pca_analysis.eigenvalues.at<double>(i, 0);//在轮廓/图像中点绘制小圆
    circle(img, pos, 3, CV_RGB(255, 0, 255), 2);
    //计算出直线，在主要方向上绘制直线（每个特征向量乘以其特征值并转换为平均位置。有一个 0.02 的缩放系数，它只是为了确保矢量适合图像并且没有 10000 像素的长度）
    line(img, pos, pos + 0.02 * Point(eigen_vecs[0].x * eigen_val[0], eigen_vecs[0].y * eigen_val[0]), CV_RGB(255, 255, 0));
    line(img, pos, pos + 0.02 * Point(eigen_vecs[1].x * eigen_val[1], eigen_vecs[1].y * eigen_val[1]), CV_RGB(0, 255, 255));
    //最终计算并返回一个最强的(即具有最大特征值）的特征向量的角度
    return atan2(eigen_vecs[0].y, eigen_vecs[0].x);
}

在图像上运行 PCA 后的结果如图，由此产生的轴是数据点差异最大的轴，这不需要反映形状的关键结构特征，尽管如此，它还是对方向的有效描述，可以获取任何形状。

4️⃣对数据集降维处理

对一副宽p、高q的二维灰度图，要完整表示该图像，需要m = p*q维的向量空间,比如100*100的灰度图像，它的向量空间为100*100=10000。下图是一个3*3的灰度图和表示它的向量表示：

该向量为行向量，共9维，用变量表示就是[v0, v1, v2, v3, v4, v5, v6, v7, v8]，其中v0...v8，的范围都是0-255。

现在的问题是假如我们用1*10000向量，表示100*100的灰度图，是否向量中的10000维对我们同样重要？肯定不是这样的，有些维的值可能对图像更有用，有些维相对来说作用小些。为了节省存储空间，我们需要对10000维的数据进行降维操作，这时就用到了PCA算法，该s算法主要就是用来处理降维的，降维后会尽量保留更有意义的维数，它的思想就是对于高维的数据集来说，一部分维数表示大部分有意义的数据。

🎈下面我们在OpenCV中看一个计算PCA的例子：

1.首先读入10副人脸图像，这些图像大小相等，是一个人的各种表情图片。

2.把图片转为1*pq的一维形式，p是图像宽，q是图像高。这时我们的S矩阵就是10行，每行是pq维的向量。

3.然后我们在S上执行PCA算法，设置K=5，求得5个特征向量，这5个特征向量就是我们求得的特征脸，用这5个特征脸图像，可以近似表示之前的十副图像。

我们输入的10副图像为：

opencv实现：

//把图像归一化为0-255，便于显示
Mat norm_0_255(const Mat& src)
{
    Mat dst;
    switch (src.channels())
    {
    case 1:
        cv::normalize(src, dst, 0, 255, NORM_MINMAX, CV_8UC1);
        break;
    case 3:
        cv::normalize(src, dst, 0, 255, NORM_MINMAX, CV_8UC3);
        break;
    default:
        src.copyTo(dst);
        break;
    }
    return dst;
}

//转化给定的图像为行矩阵
Mat asRowMatrix(const vector<Mat>& src, int rtype, double alpha = 1, double beta = 0)
{
    //样本数量
    size_t n = src.size();
    //如果没有样本，返回空矩阵
    if (n == 0)
        return Mat();
    //样本的维数
    size_t d = src[0].total();

    Mat data(n, d, rtype);
    //拷贝数据
    for (int i = 0; i < n; i++)
    {

        Mat xi = data.row(i);
        //转化为1行，n列的格式
        if (src[i].isContinuous())
        {
            src[i].reshape(1, 1).convertTo(xi, rtype, alpha, beta);
        }
        else {
            src[i].clone().reshape(1, 1).convertTo(xi, rtype, alpha, beta);
        }
    }
    return data;
}

int main(int argc, const char *argv[])
{
    vector<Mat> db;
    db.push_back(imread("D:/opencv练习图片/s1/1.png", IMREAD_GRAYSCALE));
    db.push_back(imread("D:/opencv练习图片/s1/2.png", IMREAD_GRAYSCALE));
    db.push_back(imread("D:/opencv练习图片/s1/3.png", IMREAD_GRAYSCALE));
    db.push_back(imread("D:/opencv练习图片/s1/4.png", IMREAD_GRAYSCALE));
    db.push_back(imread("D:/opencv练习图片/s1/5.png", IMREAD_GRAYSCALE));
    db.push_back(imread("D:/opencv练习图片/s1/6.png", IMREAD_GRAYSCALE));
    db.push_back(imread("D:/opencv练习图片/s1/7.png", IMREAD_GRAYSCALE));
    db.push_back(imread("D:/opencv练习图片/s1/8.png", IMREAD_GRAYSCALE));
    db.push_back(imread("D:/opencv练习图片/s1/9.png", IMREAD_GRAYSCALE));
    db.push_back(imread("D:/opencv练习图片/s1/10.png", IMREAD_GRAYSCALE));

    // Build a matrix with the observations in row:
    Mat data = asRowMatrix(db, CV_32FC1);

    // PCA算法保持5主成分分量
    int num_components = 5;

    //执行pca算法
    PCA pca(data, Mat(), 0, num_components);

    //copy  pca算法结果
    Mat mean = pca.mean.clone();
    Mat eigenvalues = pca.eigenvalues.clone();
    Mat eigenvectors = pca.eigenvectors.clone();

    //均值脸
    imshow("avg", norm_0_255(mean.reshape(1, db[0].rows)));

    //五个特征脸
    imshow("pc1", norm_0_255(pca.eigenvectors.row(0)).reshape(1, db[0].rows));
    imshow("pc2", norm_0_255(pca.eigenvectors.row(1)).reshape(1, db[0].rows));
    imshow("pc3", norm_0_255(pca.eigenvectors.row(2)).reshape(1, db[0].rows));
    imshow("pc4", norm_0_255(pca.eigenvectors.row(3)).reshape(1, db[0].rows));
    imshow("pc5", norm_0_255(pca.eigenvectors.row(4)).reshape(1, db[0].rows));

    waitKey(0);
    return 0;
}