opencv——几何变换原理与实现

摘要

图像几何变换又称为图像空间变换，它将一幅图像中的坐标位置映射到另一幅图像中的新坐标位置。几何变换不改变图像的像素值，只是在图像平面上进行像素的重新安排。

几何变换大致分为仿射变换、投影变换、极坐标变换，完成几何变换需要两个独立的算法过程：

1、一个用来实现空间坐标变换的算法，用它描述每个像素如何从初始位置移动到终止位置

2、一个插值算法完成输出图像的每个像素的灰度值

放射变换

😀首先，先来分析一下放射变换的原理：

什么是放射变换？

仿射变换是从一个二维坐标系变换到另一个二维坐标系，属于线性变换。通过已知3对坐标点可以求得变换矩阵。(不共线的三对对应点，决定了唯一的变换矩阵）

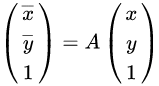其中

$A$ 就是仿射变换矩阵一般形式，根据不同的变换，比如平移、缩放、旋转等等，仿射变换矩阵的值是不一样的。

1、平移

假设空间坐标 (x，y)先沿 x轴平移t_x ,在沿 y轴平移 t_y,则变换后的坐标为（x+t_x，y+t_y） ,此时平移变换为：

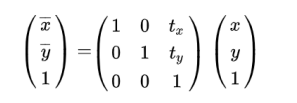
2、缩放

二维空间坐标 (x，y) 以任意一点 (x₀，y₀) 为中心在水平方向和垂直方向上分别缩放 s_x和 s_y倍，缩放后坐标为 (x₀+s_x (x-x₀)，y₀+s_y(y-y₀)) ，通俗来讲就是缩放后的坐标离中心点的水平距离变为原坐标离中心点水平距离的 s_x 倍。

当 (x₀，y₀) 为原点 (0，0）时，缩放变换可以表示为：

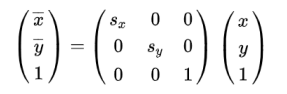
当 (x₀，y₀) 为任意点时，变换过程理解为，先将中心点平移到原点，再以原点为中心进行缩放，然后移回到原来的中心点。缩放变换表示为：

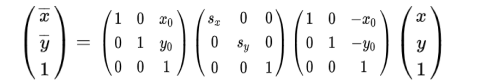
注意：等式右边的运算应该从右往左看

3、旋转

顺时针绕原点(0，0)旋转变换的矩阵表示为：

若以任意一点 (x₀，y₀) 为中心旋转，相当于先将原点移动到旋转中心，然后绕原点旋转，最后移回坐标原点，用矩阵表示为：

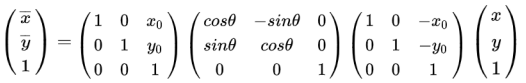
注意：上面的运算顺序是从右向左的。

OpenCV提供的旋转函数，实现顺时针90°、180°、270°的旋转

rotate(InputArray src, Output dst, int rotateCode)

rotateCode有以下取值：
ROTATE_90_CLOCKWISE    //顺时针旋转90度
ROTATE_180             //顺时针旋转180度
ROTATE_90_COUNTERCLOCKWISE  //逆时针旋转90度

需要注意的是OpenCV还有一个函数为flip(src, dst, int flipCode)实现了图像的水平镜像、垂直镜像和逆时针旋转180°，不过并不是通过仿射变换实现的，而是通过行列互换，它与rotate()、transpose()函数一样都在core.hpp头文件中。

求解放射变换矩阵

以上都是知道变换前坐标求变换后的坐标，如果我们已经知道了变换前的坐标和变换后的坐标，想求出仿射变换矩阵，可以通过解方程法或矩阵法。

🤨解方程法

由于仿射变换矩阵

有6个未知数，所以我们只需三组坐标列出六个方程即可。OpenCV提供函数getAffineTransform(src, dst)通过方程法求解，其中src和dst分别为前后坐标。

对于C++来说，一种方式是将坐标存在Point2f数组中，另一种方法是保存在Mat中：

// 第一种方法
Point2f src1[] = {Pointy2f(0, 0), Point2f(200, 0), Point2f(0, 200)};
Point2f dst1[] = {Pointy2f(0, 0), Point2f(100, 0), Point2f(0, 100)};
// 第二种方法
Mat src2 = (Mat_<float>(3, 2) << 0, 0, 200, 0, 0, 200);
Mat dst2 = (Mat_<float>(3, 2) << 0, 0, 100, 0, 0, 100);

Mat A = getAffineTransform(src1, dst1);

😮矩阵法

对于等比例缩放的仿射变换，OpenCV提供函数getRotationMatrix2D(center, angle, scale)来计算矩阵，center是变换中心；angle是逆时针旋转的角度，（opencv中正角度代表逆时针旋转）；scale是等比例缩放的系数。

我们通过下面的代码来定义这些参数，例如：

Point center = Point( src.cols/2, src.rows/2 ); //中心点
double angle = -50.0;
double scale = 0.6;

插值算法分析

在运算中，我们可能会遇到目标坐标有小数的情况，比如将坐标(3，3)缩放2倍变为了(1.5，1.5)，但是对于图像来说并没有这个点，这时候我们就要用周围坐标的值来估算此位置的颜色，也就是插值。

（1）最近邻插值（INTER_NEAREST)

最近邻插值就是从(x，y)的四个相邻坐标中找到最近的那个来当作它的值，如(2.3，4.7)，它的相邻坐标分别为(2，4)、(3，4)、(2，5)、(3，5)，计算这几个相邻坐标与(2.3，4.7)坐标的距离，若最近的为(2，5)，则取(2，5)的颜色值为的(2.3，4.7)值。

此种方法得到的图像会出现锯齿状外观，对于放大图像则更明显。

（2）双线性插值（INTER_LINEAR）（最常用）

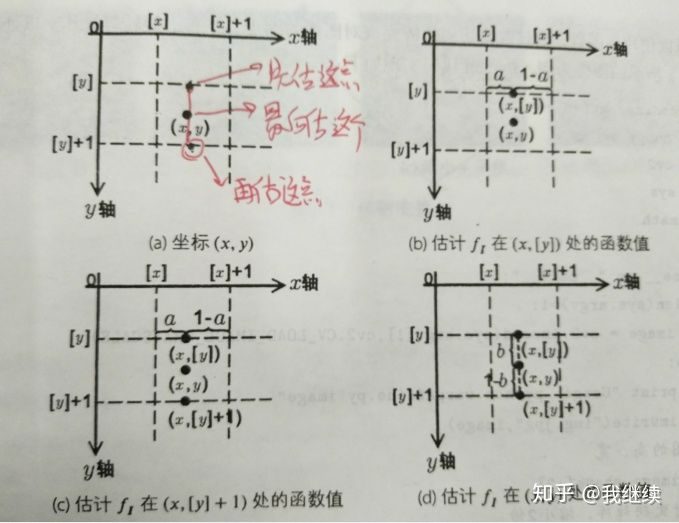
要估计输入图像非整数坐标 $(x,y)$ 的值，分为三个步骤:

第一步：先用线性关系估计输入图像中 $(x,[y])$ 的值

$\frac{f(x,[y])-f([x],[y])}{a} = \frac{f([x]+1,[y])-f([x],[y])}{1}$ $f(x,[y]) = af([x]+1,[y])+(1-a)f([x],[y])$

第二步：同理用线性关系估计输入图像中 $(x,[y]+1)$ 的值

$f(x,[y]+1) = af([x]+1,[y]+1)+(1-a)f([x],[y]+1)$

第三步：根据前两步得到的值，用线性关系估计输入图像中 $(x,y)$ 的值

$f(x,y) = b(f(x,[y]+1)+(1-b)f(x,[y])$

进行放射变换

将刚刚求得的仿射变换矩阵应用到原图像，OpenCV提供函数warpAffine进行放射变换。

warpAffine(src，dst，M，dsize，flags，bordMode, borderValue)
//src:输入图像
//dst：输出变换后图像，需要初始化一个空矩阵用来保存结果，不用设定矩阵尺寸
//M：2行3列的仿射变换矩阵
//dsize: 二元元组(宽，高)，代表输出图像大小
//flags: 插值法 INTER_NEAREST、INTER_LINEAR(默认线性插值)
//bordMode: 边界像素模式，默认值BORDER_CONSTANT
//bordValue: 当填充模式为BORDER_CONSTANT时的填充值（默认为Scalar（），即0）

opencv实现放射变换

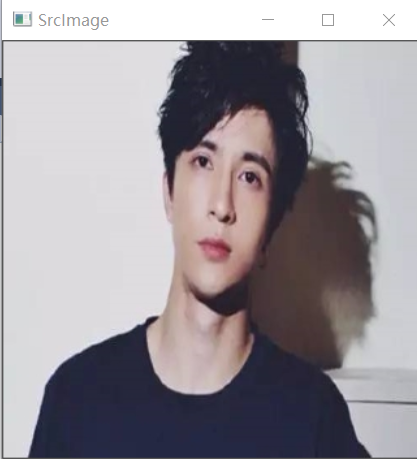
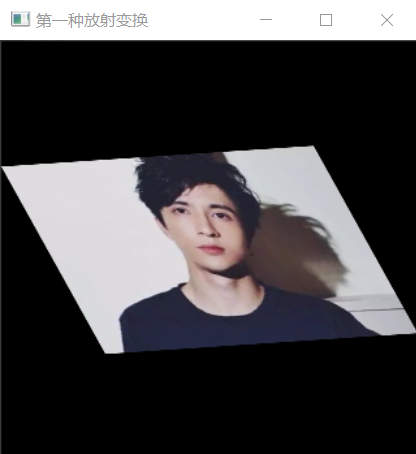
1️⃣第一种仿射变换的调用方式：三点法

说明：当得到变换前的三点坐标以及变化后的三点坐标就可以用该方法

    Point2f srcPoints[3];//原图中的三点 (一个包含三维点（x，y）的数组，其中x、y是浮点型数)
    Point2f dstPoints[3];//目标图中的三点 
    Mat dst_warp1, dst_warp2;
    Mat src = imread("D:/opencv练习图片/薛之谦.jpg");
    imshow("输入图像", src);
    //第一种仿射变换的调用方式：三点法
   //三个点对的值,上面也说了，只要知道你想要变换后图的三个点的坐标，就可以实现仿射变换 
    srcPoints[0] = Point2f(0, 0);
    srcPoints[1] = Point2f(0, src.rows);
    srcPoints[2] = Point2f(src.cols, 0);
    //映射后的三个坐标值
    dstPoints[0] = Point2f(0, src.rows*0.3);
    dstPoints[1] = Point2f(src.cols*0.25, src.rows*0.75);
    dstPoints[2] = Point2f(src.cols*0.75, src.rows*0.25);
    Mat M1 = getAffineTransform(srcPoints, dstPoints);//由三个点对计算变换矩阵 
    warpAffine(src, dst_warp1, M1, src.size());//仿射变换
    imshow("放射变换", dst_warp1);

2️⃣第二种仿射变换的调用方式：自定义旋转角度和缩放比例（最常用）

说明：angle（旋转角度：正数为逆时针旋转，负数为顺时针旋转）；scale（缩放因子）

    Mat src = imread("D:/opencv练习图片/薛之谦.jpg");
    imshow("输入图像", src);
    /// 计算关于图像中心的旋转矩阵
    Point center = Point(src.cols / 2, src.rows / 2);
    double angle = 35.0;
    //旋转的同时也可以放缩
    double scale = 0.8;
    /// 根据以上参数得到旋转矩阵
    Mat M = getRotationMatrix2D(center, angle, scale);
    //计算旋转后的画布大小，并将旋转中心平移到新的旋转中心
    Rect bbox = RotatedRect(center, Size(src.cols*scale, src.rows*scale), angle).boundingRect();
    M.at<double>(0, 2) += bbox.width / 2.0 - center.x;
    M.at<double>(1, 2) += bbox.height / 2.0 - center.y;
    /// 旋转图像
    Mat rotate_dst;
    warpAffine(src, rotate_dst, M, bbox.size());
    imshow("放射变化", rotate_dst);
    waitKey(0);
    return 0;

💖分析：

对于该句的理解：

//计算旋转后的画布大小，并将旋转中心平移到新的旋转中心
    Rect bbox = RotatedRect(center, Size(src.cols*scale, src.rows*scale), angle).boundingRect();
    M.at<double>(0, 2) += bbox.width / 2.0 - center.x;
    M.at<double>(1, 2) += bbox.height / 2.0 - center.y;

是由于在图像旋转之后，部分数据就会超出原来图像的位置，出现截断，为了避免上面的问题，引入类RotatedRect。并计算它的外接矩形（使用成员函数boundingRect()返回）

最后计算新的中心点

格外注意：size（src.cols*scale,src.rows*scale）对于中心点坐标（而不是像素坐标）

小结（对于opencv中“旋转”的思考）

很多人都对opencv中的旋转吐糟，意思是它自己没有很好的关于选择的算法。那么今天就来分析一下OpenCV中旋转是如何定量的，什么是正方向？什么是负方向？什么时候用角度？什么时候用弧度？

一、OpenCV中旋转式如何定量的

也就是坐标系问题。OpenCV坐标系以(0,0)点为原点（也就是左上角那个点），以向下为Y轴正方向，以向右为X轴正方向。

对于旋转而言，通过“旋转中点”和“旋转的角度”两个值来定量一个“旋转”。

二、什么是正方向？什么是负方向？什么时候用角度？什么时候用弧度？

一般来说，坐标系中以X轴正方向为原点，而以逆时针为正、顺时针为负。

至于什么时候用角度、什么时候用弧度，一般来说，角度180度对应于弧度的PI,由于在使用函数的时候，一般只能以数值类型（不带单位）作为参数，所以需要根据函数自己的要求选择弧度还是角度.

三、相关的函数和使用方法

可能这才是最为关键的。我这样来归纳。

void rotate(InputArray src, OutputArray dst, int rotateCode);
getRotationMatrix2D函数
通过pca获得图像的弧度（这个函数的目的，在于通过PCA方法，获得当前轮廓的主要方向。）

投影变换（透视变换）

如果物体在三维空间中发生旋转，这种变换通常成为投影变换。

投影变换的API和仿射变换的API很像，原理也相同，不同的只是由之前的三点变为四点法求投影变换矩阵，变换矩阵也由2*3变为3*3；可以通过以下公式表述：

OpenCV提供函数getPerspectiveTransform(src, dst)实现求解投影矩阵，需要输入四组对应的坐标。

getPerspectiveTransform(const Point2f* src, const Point2f* dst)
    //参数const Point2f* src：原图的四个固定顶点
    //参数const Point2f* dst：目标图像的四个固定顶点
    //返回值：Mat型变换矩阵，可直接用于warpAffine()函数
    //注意，顶点数组长度超4个，则会自动以前4个为变换顶点；数组可用Point2f[]或Point2f*表示

OpenCV提供函数warpPerspective实现投影变换，参数说明和仿射变化类似。

warpPerspective(src，dst，M，dsize，flags，bordMode, borderValue)
//src:输入图像
//dst：输出变换后图像，需要初始化一个空矩阵用来保存结果，不用设定矩阵尺寸
//M：2行3列的仿射变换矩阵
//dsize: 二元元组(宽，高)，代表输出图像大小
//flags: 插值法 INTER_NEAREST、INTER_LINEAR(默认线性插值)
//bordMode: 边界像素模式，默认值BORDER_CONSTANT
//bordValue: 当填充模式为BORDER_CONSTANT时的填充值（默认为Scalar（），即0）

😛opencv实现投影变换：

Mat src, dst_warp1;
Point2f srcPoints[4];//原图中的三点 (一个包含三维点（x，y）的数组，其中x、y是浮点型数)
Point2f dstPoints[4];//目标图中的三点  

int main(int argc, char** argv)
{            
    src = imread("D:/opencv练习图片/薛之谦.jpg");
    namedWindow("SrcImage");
    imshow("SrcImage", src);
    //变换前四点坐标
    srcPoints[0] = Point2f(0, 0);
    srcPoints[1] = Point2f(0, src.rows);
    srcPoints[2] = Point2f(src.cols, 0);
    srcPoints[3] = Point2f(src.cols, src.rows);
    //变换后的四点坐标
    dstPoints[0] = Point2f(src.cols*0.1, src.rows*0.1);
    dstPoints[1] = Point2f(0, src.rows);
    dstPoints[2] = Point2f(src.cols, 0);
    dstPoints[3] = Point2f(src.cols*0.7, src.rows*0.8);
    Mat M1 = getPerspectiveTransform(srcPoints, dstPoints);//由四个点对计算透视变换矩阵  
    warpPerspective(src, dst_warp1, M1, src.size());//投影变换  
    imshow("投影变换（四点法）", dst_warp1);    
    waitKey(0);
    return 0;
}

极坐标变换

通常通过极坐标变化校正图像中的圆形物体或包含在圆环中的物体。

OpenCV 中提供了warpPolar()函数用于实现图像的极坐标变换，该函数的函数原型如下：

warpPolar( src, dst, Size dsize, Point2f center, double maxRadius, int flags )

src：原图像，可以是灰度图像或者彩色图像

dst：极坐标变换后输出图像（与原图像具有相同的数据类型和通道数）。

dsize：输出图像大小。(自行决定)

center：极坐标变换时极坐标原点在原图像中的位置。

maxRadius：变换时边界圆的半径，它也决定了逆变换时的比例参数。

flags：插值方法与极坐标映射方法标志，两个方法之间通过“+”或者“|”号进行连接。

😄warpPolar()函数极坐标映射方法标志：

WARP_POLAR_LINEAR     //极坐标正变换（直角坐标变换到极坐标）
WARP_POLAR_LOG         //半对数极坐标变换
WARP_INVERSE_MAP     //逆变换（极坐标变换到直角坐标）

😛opencv实现极坐标变换：

Mat src, dst;
int main(int argc, char** argv)
{            
    src = imread("D:/opencv练习图片/环形字符.jpg");
    namedWindow("SrcImage");
    imshow("SrcImage", src);
    Point2f center = Point2f(src.cols / 2, src.rows / 2); //极坐标在图像中的原点    
    // 圆的半径
    double maxRadius = min(center.y, center.x);
    //正极坐标变换
     warpPolar(src, dst, Size(200, 500), center, maxRadius, INTER_LINEAR | WARP_POLAR_LINEAR);
    // 改变结果方向
    rotate(dst, dst, ROTATE_90_COUNTERCLOCKWISE);
    imshow("极坐标变换", dst);
    waitKey(0);
    return 0;
}