最优前缀编码

1. 问题

2. 解析

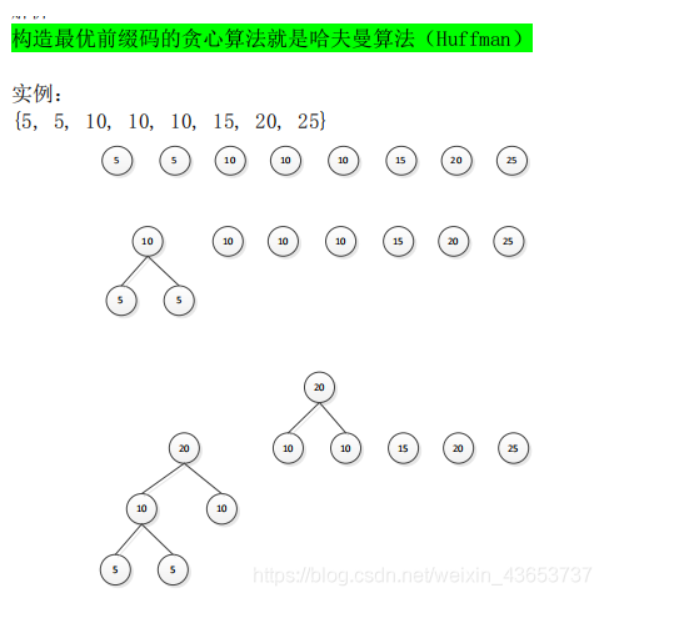
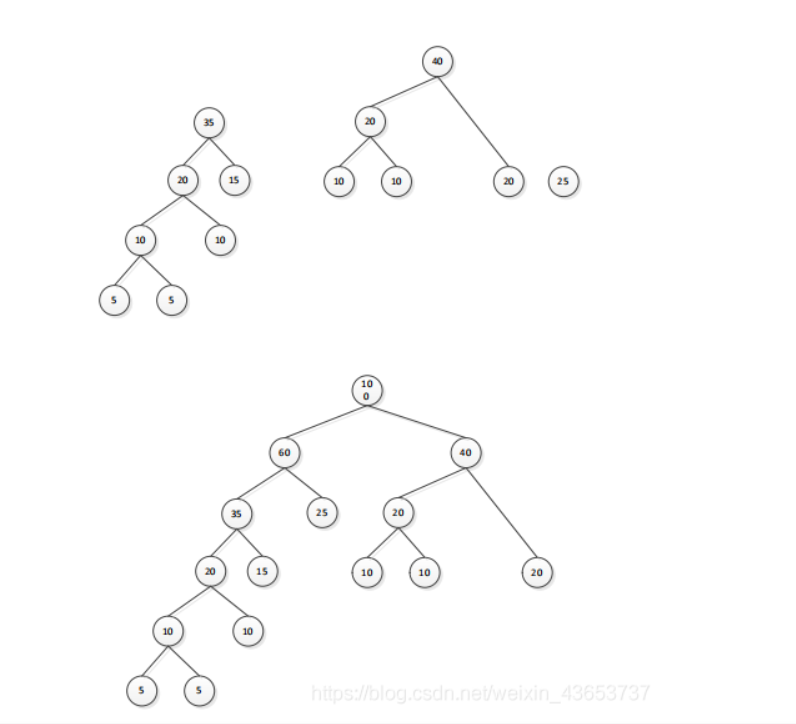
3. 设计

//根据哈夫曼树T求哈夫曼编码表H

void CharSetHuffmanEncoding(HuffmanTree T, HuffmanCode H) {

int c, p;//c和p分别指示T中孩子和双亲的位置

char cd[n + 1];//临时存放编码

int start;//指示编码在cd中的起始位置

cd[n] = '\0';//编码结束符

getchar();

for (int i = 0; i < n; i++) {//依次求叶子T[i]的编码

H[i].ch = getchar();//读入叶子T[i]对应的字符

start = n;//编码起始位置的初值

c = i;//从叶子T[i]开始上溯

while ((p = T[c].parent) >= 0) {//直至上溯到T[c]是树根为止

//若T[c]是T[p]的左孩子，则生成代码0；否则生成代码1

if (T[p].lchild == c)

cd[--start] = '0';

else

cd[--start] = '1';

c = p;//继续上溯

}

strcpy_s(H[i].bits, &cd[start]);//复制编码位串

}

void CreateHuffmanTree(HuffmanTree T) {

//构造哈夫曼树，T[m-1]为其根结点

int i, p1, p2;

InitHuffmanTree(T); //将T初始化

InputWeight(T); //输入叶子权值

for (i = n; i < m; i++) {

//在当前森林T[0．．i-1]的所有结点中，选取权最小和次小的

//两个根结点T[p1]和T[p2]作为合并对象

//共进行n-1次合并，新结点依次存于T[i]中

SelectMin(T, i - 1, &p1, &p2);//选择权值最小和次小的根结点，其序号分别为p1和p2

//将根为T[p1]和T[p2]的两棵树作为左右子树合并为一棵新的树

//新树的根是新结点T[i]

T[p1].parent = T[p2].parent = i;//T[p1]和T[p2]的两棵树的根结点指向i

T[i].lchild = p1; //最小权的根结点是新结点的左孩子

T[i].rchild = p2; //次小权的根结点是新结点的右孩子

T[i].weight = T[p1].weight + T[p2].weight;//新结点的权值是左右子树的权值之和

}

4. 分析

O(nlogn)频率排序：
for 循环 O(n)，
插入操作 O(logn)，
算法时间复杂度是 O(nlogn)

5. 源码

#include<cstdio>

#include<cstdlib>

#include<cstring>

#include<algorithm>

using namespace std;

#define n 8 //叶子数目

#define m 2*n-1 //树中结点总数

typedef struct { //结点类型

double weight; //结点的权值

int parent, lchild, rchild;//双亲指针及左右孩子

}HTNode;

typedef HTNode HuffmanTree[m];//HuffmanTree是向量类型

typedef struct { //用于SelectMin函数中排序的结点类型

int id; //保存根结点在向量中的序号

double weight; //保存根结点的权值

}temp;

typedef struct { //编码结点

char ch; //存储字符

char bits[n + 1]; //存放编码位串

}CodeNode;

typedef CodeNode HuffmanCode[n];

//初始化哈夫曼树

void InitHuffmanTree(HuffmanTree T) {

for (int i = 0; i < m; i++) {

T[i].lchild = -1;

T[i].rchild = -1;

T[i].parent = -1;

T[i].weight = 0;

}

//输入叶子权值

void InputWeight(HuffmanTree T) {

for (int i = 0; i < n; i++) {//读人n个叶子的权值存于向量的前n个分量中

double x;

scanf_s("%lf", &x);

T[i].weight = x;

}

//用于排序的比较函数

bool cmp(temp a, temp b) {

return a.weight < b.weight;

}

//在前k个结点中选择权值最小和次小的根结点，其序号分别为p1和p2

void SelectMin(HuffmanTree T, int k, int* p1, int* p2) {

temp x[m]; //x向量为temp类型的向量

int i, j;

for (i = 0, j = 0; i <= k; i++) { //寻找最小和次小根节点的过程

if (T[i].parent == -1) {//如果是根节点,则进行如下操作

x[j].id = i; //将该根节点的序号赋值给x

x[j].weight = T[i].weight;//将该根节点的权值赋值给x

j++; //x向量的指针后移一位

}

sort(x, x + j, cmp); //对x按照权值从小到大排序

//排序后的x向量的第一和第二个位置中存储的id是所找的根节点的序号值

*p1 = x[0].id;

*p2 = x[1].id;

}