装载问题
1. 问题
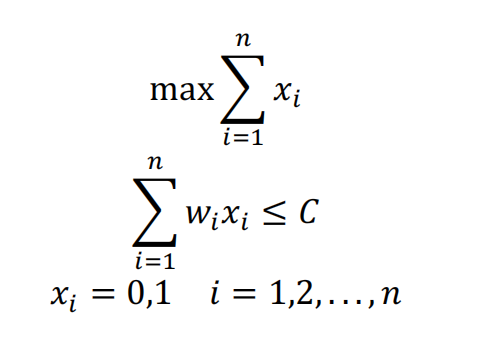
整数规划问题,0-1 背包问题
2. 解析
思路:轻者先装,直到再装任何集装箱将使轮船载重量超过 C 时停止。
定理:对于任何正整数 k,算法(轻者先装)对 k 个集装箱的实例得到
最优解。
证明:(数学归纳法)
(1)k=1,只有 1 个集装箱,其重量小于 C。任何装法都只有一种方式,
因此都是最优解,因此轻者先装也是最优解。
(2)归纳假设:假设算法对于规模为 k 的输入都能得到最优解。
考虑规模为 k+1 的输入, N={1,2,...,k+1},W={w1,w2,...,wk+1}是集装箱的重量,w1,w2,...,wk+1 。
从 N 中拿掉最轻的集装箱,得到 k 规模的输入:
N’=N-{1}={2,3,4,...,k+1}
W’=W-{w1}
C’=C-w1
根据归纳假设,对于 k 个输入,N’、W’、C’的最优解为 I’,即
I’为 N’,不含 1 的最优解(归纳假设得),
令 I=I’U{1}
那么 I 必然是 N 的最优解,这也是算法对于 N,W,C 的解。
证明:I 必然是 N 的最优解,采用反证法,即假设 I 不是 N 的最优解。
(1)构建最优解 I*(N,含 1):假设 I 不是 N 的最优解。则必然存在
最优解 I*,如果 I*中没有 1,用 1 替代 I*中的第一个集装箱标号得到的解也是
最优解(个数不变,因此也是最优解),使得 I*为包含 1 的关于 N 的最优解,
且|I*|>|I|。
(2) 构建最优解 I*’( N’,不含 1):因为 I*为包含 1 的关于 N
的最优解,构建的 I*’=I*-{1}是不包含 1 的最优解(待证明),即关于 N’、
W’、C’的最优解(N’、W’、C’不包含 1)。
证明:I*’=I*-{1}是不包含 1 的最优解。
证(反证法):如果 I*’=I*-{1}不是不包含 1 的最优解,那么存在最优
解 I*’’ ( N’,不含 1),使得|I*’|<|I*’’|,
即|I*’+{1}|<|I*’’ +{1}|,与 I*’+{1}= I*为最优矛盾,因此
I*’=I*-{1}是不包含 1 的最优解。
(3)构建的最优解 I*’与归纳假设的最优解 I’比较:由(1)
|I*|>|I|得,| I*’|= |I*-{1}|>|I-{1}|=|I’|,与 I’的最优性矛盾(最优解 I*-
{1}大于最优解 I’)。
3. 设计
4. 分析
O(nlogn)
5. 源码
#include<stdio.h>
#define M 100
int n=3;
int x[]={0,0,0};
int c1=50;
int w[]={10,40,40};
int x1[]={0,0,0};
int Constrain(int t){
int i;
int sum=0;
static int sum1=0;
for(i=0;i<=t;i++){
if(x[i]==1)
sum+=w[i];
}
printf("--------------->%d\n",sum);
for(i=0;i<n;i++){
printf("%d",x1[i]);
}
printf("\n");
if(sum>c1){
x[t]=0;
return 0;
}
else {
if(sum1<sum){
for(i=0;i<=t;i++){
if(x[i]==1) x1[i]=1;
else x1[i]=0;
}
}
return 1;
}
}
int Bound(int t){
if(t<n)
return 1;
else return 0;
}
void Backtrack(int t){
int i;
if(t<n){
for(i=0;i<=1;i++){
x[t]=i;
if(Constrain(t)&&Bound(t))
Backtrack(t+1);
}
}
}
int main(){
int i;
int sum=0;
Backtrack(0);
for(i=0;i<n;i++){
if(x1[i]==0)
sum+=w[i];
}
if(sum>c1){
printf("无解");
return 0;
}
for(i=0;i<n;i++){
if(x1[i]==1)
printf("%d ",w[i]);
}
}



